데이터 분석 - 회귀 분석

회귀 분석

• 통계학에서 사용되는 방법 중 하나, 두 변수 사이의 관계를 모델링하는 방법

  독립 변수가 종속 변수에 어떤 영향을 미치는지 알아볼 수 있음 ex) 원인과 결과

독립 변수	종속 변수
종속변수에 영향을 주는 변수 '설명변수', '예측변수', '특징'	우리가 예측하거나 설명하려는 대상 변수 '반응변수', '결과변수'

회귀 분석 기본 가정

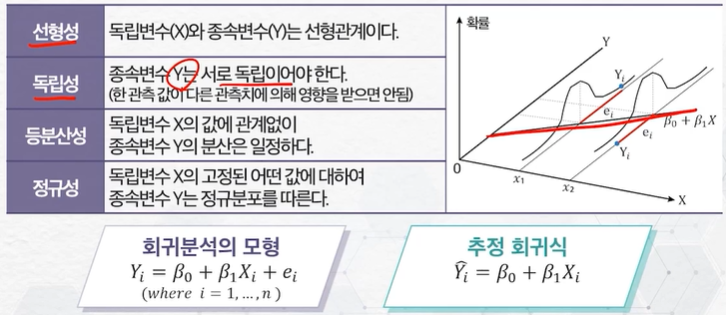
최소제곱법

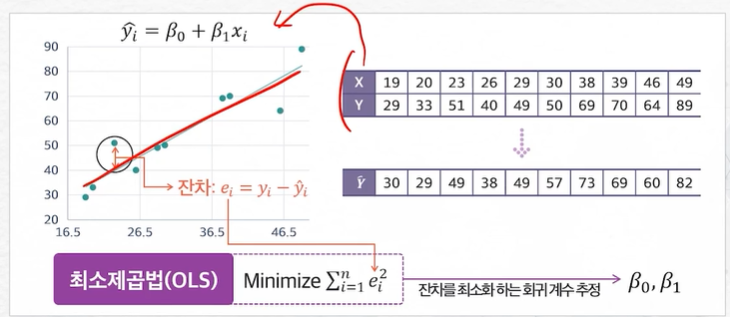
t검정

단순회귀계수를 검정할 때,
개별회귀계수의 통계적 유의성은 t검정으로 확인

다중 회귀분석

• 단순회귀분석의 확장으로 독립변수가 두 개 이상인 회귀모형에 대한 분석

이차 회귀모델

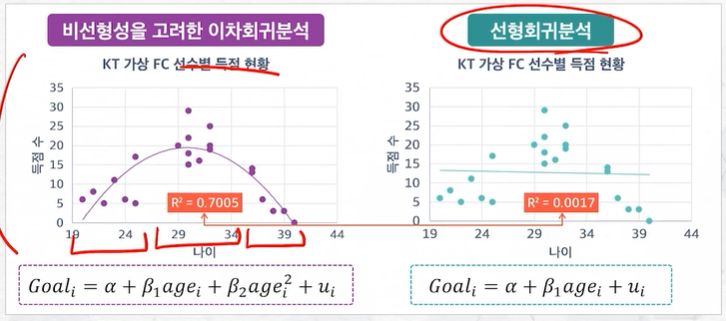
다항 회귀모델

• 3차, 4차 등 있음
  

---

회귀분석

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from scipy import stats
import statsmodels.api as sm #회귀분석을 위한

#데이터셋 로딩
boston_df = pd.read_csv('./data/boston.csv')

단순 회귀

주택 가격(중앙값)을 하위 소득 계층 비율로 설명하려고 하는 단순 회귀 식
MEDV = β0 + β1LSTAT + e
- 종속변수 : MEDV
- 독립변수 : LSTAT

# 두 변수간 관계 파악을 위한 산점도
sns.scatterplot(x=boston_df['LSTAT'], y=boston_df['MEDV'])
plt.show()

# 종속변수와 독립변수 설정
MEDV = boston_df['MEDV'].values
LSTAT = boston_df['LSTAT'].values

독립변수에 상수항 결합

#회귀모형 수식을 간단히 만들귀 위해 상수항을 독립변수에 추가해줘야함
#상수항이 결합되면 원소가 1인 데이터가 추가됨
#상수항이 결합되어야 가중치 beta_0이 행렬곱으로 들어왔을때, 살아남음 -> 수식 간단해짐
# 일반적으로 선형회귀는 늘 상수항 결합을 함

LSTAT = sm.add_constant(LSTAT)

단순 선형 회귀 분석

linear_mod = sm.OLS(MEDV, LSTAT) #statsmode 의 OLS를 이용해 종속,독립변수를 인수로 추가

linear_mod #인스턴스
linear_result = linear_mod.fit()

print(linear_result.summary()) #summary = 회귀결과를. 

np.sqrt(linear_result.fvalue) #모델의 설명력을 평가해주는 검정통계량

#R스타일로 리그레션 - from_formula이용
linear_mod = sm.OLS.from_formula("MEDV","LSTAT", data=boston_df)
linear_result = linear_mod.fit()

#잔차 확인
#잔차의 분포 확인
sns.histplot(linear_result.resid)
plt.show()

선형화를 통한 회귀 분석

상관관계 및 분포 확인
#하위 계층 비율과 집 거래 중앙값 관계 확인
sns.pairplot(boston_df[['LSTAT', 'MEDV']])
plt.show()

#LSTAT의 log 변환
sns.scatterplot(x=np, log(boston_df['LSTAT']), y=boston_df['MEDV'])

회귀 분석

#로그 변환 후 회귀 분석 진행
log_linear_mod = sm.OLS.from_formula("MEDV ~ np.log(LSTAT)", data=boston_df)
log_linear_result = log_linear_mod.fit()

#summary table 출력
print(log_linear_result.summary())

#잔차 확인
sns.histplot(log_linear_result.resid)
plt.show()

2차 회귀 분석 (Quadratic Regression Model)

sns.pairplot(boston_df[['LSTAT','MEDV']])
plt.show()

#2차 회귀 분석 모델 설정
quadratic_mod = sm.OLS.from_formula("MEDV ~ LSTAT + I(LSTAT ** 2)", data=boston_df) #LSTAT의 제곱값 추가, I = 인트렉션
quadratic_result = quadratic_mod.fit()

잔차 확인
sns.histplot(quadratic_result.resid)

3개 모델 결과 비교 (선형 vs 로그-리니어 vs 2차회귀)

print(np.round(linear_result.rsquared, 2))
print(np.round(log_linear_result.rsquared, 2))
print(np.round(quadratic_result.rsquared, 2))

다중 회귀 (Multiple Regression)

sns.pairplot(boston_df[['LSTAT', 'RM', 'MEDV']])
plt.show()

#RM 변수 추가시 두가지 옵션, 이미 평균값이기에 수치형으로 볼 수 있음
#하지만 범주형 변수임, 한개두개세개..2.5개 와 같은 실수는 취할 수 없음 이럴땐 binning처리 가능
multi_model = sm.OLS.from_formula("MEDV ~ RM + LSTAT + I(LSTAT ** 2)", data=boston_df)
multi_result = multi_model.fit()
print(multi_result.summary())

#잔차 확인
sns.histplot(multi_result.resid())
plt.show()

#로그항 추가 (2차항 제거)
multi_mod2 = sm.OLS.from_formula("MEDV ~ RM + np.log(LSTAT)", data=boston_df)
multi_result2 = multi_mod2.fit()
print(multi_result2.summary())

#잔차 확인
sns.histplt(multi_result2.resid)
plt.show()

#성능확인
print(np.round(multi_result.rsquared, 2))
print(np.round(multi_result2.rsquared, 2))