https://arxiv.org/abs/2006.11239

DDPM 이란

---

기존의 Diffusion 모델들은 뛰어난 성능을 지녔지만, foward process중 분산을 설정하거나 reverse process중 가우시안 분포의 여러 매개변수들을 설정해줘야 한다는 단점이 존재하였다. 따라서 DDPM 에서는 기존의 Diffusion 모델과 denoising score matching 방법을 결합하여 더욱 더 단순화된 diffusion 모델을 제안하였다.

Background

---

DDPM 모델을 설명하기에 앞서 Diffusion 모델의 구조를 먼저 살펴보자

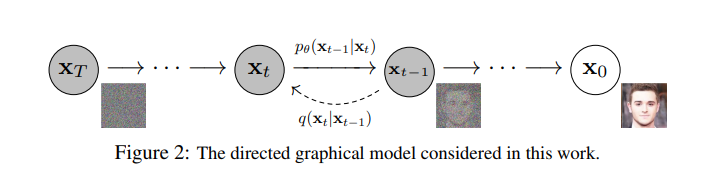
주어진 input에서 부터 서서히 가우시안 noise를 더해나가는 과정을 forward process 라고 한다. 이와는 반대로 noise로 부터 원래의 이미지로 돌아가는 과정을 reverse process 또는 backward process 라고 한다. 이미지에서 노이즈를 더해 가는 과정인 forward process는 비교적 쉽게 정의할 수 있지만 노이즈로 부터 이미지를 만들어내는 과정인 backward process는 정의하기가 쉽지 않다. 따라서 backward process를 어떻게 학습하는지가 상당히 중요한 요소가 된다. 이렇게 backward process를 학습하는 모델이 diffusion probabilistic model이다.

Forward process

Forward process는 markov chain으로 input data인 $x_0$로부터 noise를 더해가면서 최종적인 완전한 노이즈로 가는 과정이다. Forward process의 과정을 수식으로 표현하면 다음과 같은 식이 나오게 된다.

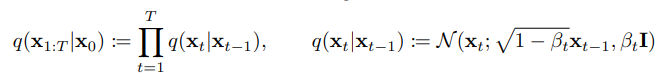
Forward process 에서는 매 step마다 가우시안 분포에서 reparameterize를 통해 sampling을 진행한 후 이를 $\sqrt{1-\beta_t}$를 곱하여 rescaling한 noise를 추가하게 된다.

🤔 $\sqrt{1-\beta_t}$를 곱하여 rescaling 하는 이유는 무엇일까?
$\sqrt{1-\beta_t}$를 곱하여 rescaling 하는 이유는 variance가 발산하는 것을 막기 위함이다.
$\beta_t$는 0과 1사이의 값으로 foward process와 reverse process 과정에서 variance가 일정수준으로 유지될 수 있게 해준다.

이렇게 매 step마다 즉 t번의 sampling을 진행하며 $x_0$부터 $x_T$를 만들어 낼 수 있지만 식을 정리하다 보면 한번에 이를 처리할 수 있다.

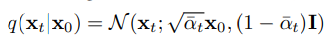
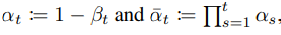
Reverse process

Reverse process는 noise된 이미지 $x_T$로부터 원본 이미지 $x_0$를 복원해 내는 과정이다. 즉 random noise로부터 data를 생성해내는 과정인 것이다. 우리가 실제로 알고싶은건 $q(x_{t-1}|x_t)$이지만 이를 실제로 알기는 어렵기 때문에 $p_\theta$를 통해 근사값을 찾아내고자 한다. $p_\theta$도 마찬가지로 markov chain 형식이며 수식으로 표현하면 다음과 같다.

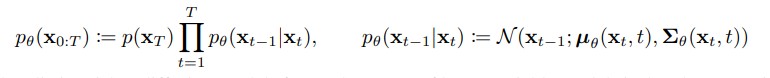
즉 우리가 여기서 학습해야 할 매개변수는 $p_\theta$의 기대값인 $\mu_\theta(x_t,t)$와 분산 $\sum_\theta(x_t,t)$이다. 또한 $p_\theta$ 과정 중 가장 첫 번째 단계인 $p(x_T)$는 다음과 같은 표준 정규분포로 정의한다.

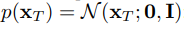
Loss function

이렇게 forward process와 reverse process에 대해 알아보았으니 실제 reverse process의 $p_\theta$는 어떻게 학습되는지 그 과정에 대해 알아보자.

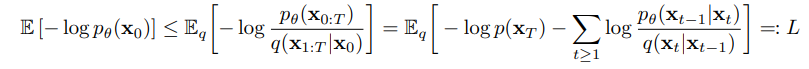
위의 식을 계산의 용이성을 위해 두 가우시안 분포 간의 KL divergence 형태로 표현하면 다음과 같은 수식이 완성된다.

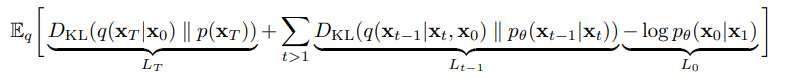
• 증명
  

$L_T$

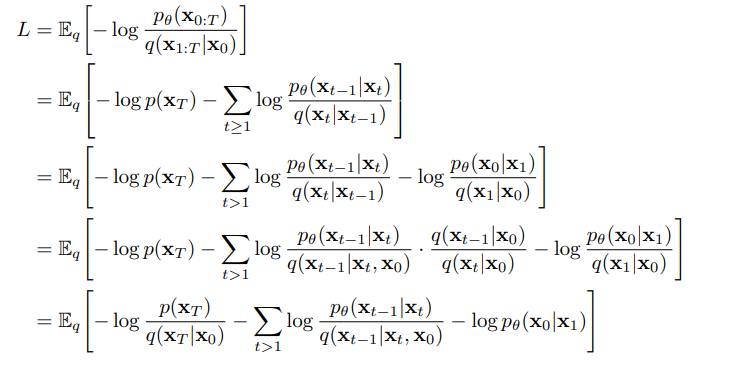
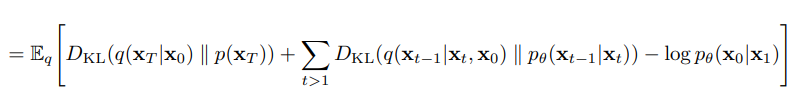
$p_\theta$가 생성해낸 노이즈인 $x_T$와 $q$가 input값인 $x_0$데이터로부터 생성된 $x_T$ 의 분포 차이를 계산해 내는 부분이다. 즉 최종적인 noise인 $x_T$의 분포를 비교하는 파트가 바로 $L_T$인 것이다.

$L_{t-1}$

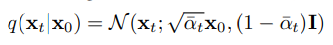
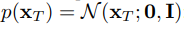
$p_\theta$와 $q$가 생성해낸 $x_{t-1}$의 분포 차이를 계산하는 부분이다. 각각의 $p_\theta$와 $q$를 확인해보면 다음과 같다.

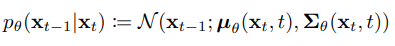
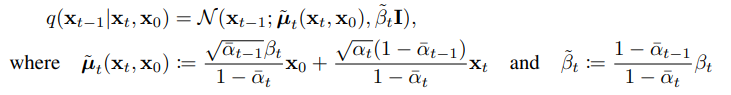
🤔 왜$q(x_t|x_{t-1})$ 대신에 $q(x_{t-1}|x_t,x_0)$를 사용할까?
현재 forward process를 진행하며 우리는 $q(x_t|x_{t-1})$의 분포를 알고 있다. 하지만 우리가 diffusion probabilistic model 즉, $p_\theta$의 매개변수를 학습하기 위해서는 $q(x_{t-1}|x_t)$의 값이 필요하다. 그 이유는 Loss function에서 ground truth 역할을 $q(x_{t-1}|x_t)$가 수행하기 때문이다.

$q(x_{t-1}|x_t,x_0)$는 베이지안 정리의 사후 확률을 이용하여 구할 수 있다.

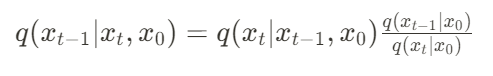
L_0

latent variable $x_1$으로부터 원본 데이터 $x_0$를 추정하는 likelihood이다.

Diffusion models and denoising autoencoders

---

앞으로 나올 내용이 본 논문의 핵심 내용이다. 이전까지는 기존의 Diffusion 모델이 어떠한 구조를 가졌고, 어떻게 학습 되는지 설명했다면, 이제부터는 어떻게 DDPM이 기존의 Diffusion model을 발전시켰는지와 어떻게 학습을 진행했는지 설명한다.

DDPM의 Loss function은 기존의 Diffusion모델과 동일하다.

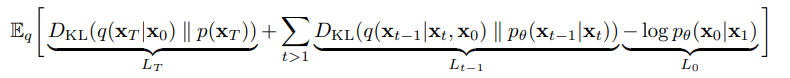
Forward process

본 논문에서는 forward process의 parameter 값인 $\beta_t$를 상수로 고정하기 때문에 Forward process의 loss term 인 $L_T$는 학습 과정에서 무시된다. 그 이유는 forward process에서 $x_T$가 항상 가우시안 분포를 따르기 때문에 $q(x_T|x_0)$는 $p(x_T)$와 유사하기 때문이다.

🤔 첫 번째 DDPM의 차이점
이렇게 forward process의 parameter 였던 $\beta_t$를 상수로 치환함으로써 학습과정을 단순화시켰다.

Reverse process

Reverse process에서는 우선 $q(x_{t-1}|x_t,x_0)$를 알아내고 $p_\theta(x_{t-1}|x_t)$를 알아내기 위해 $p_\theta$의 매개변수인 $\sum_\theta$와 $\mu_\theta$를 알아내야 한다.

매개변수

1. $q(x_{t-1}|x_t,x_0)$

기존의 Diffusion 모델과 동일하다.

2. $p_\theta(x_{t-1}|x_t)$

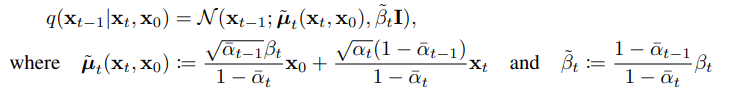
기존의 Diffusion 모델과 형태가 동일하지만 매개변수는 다시 reparameterize를 진행한다.

3. $\sum_\theta(x_t,t)$

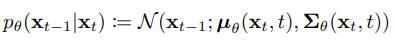
기존의 Diffusion 모델과는 다르게 $p_\theta$의 매개변수 중 하나인 표준편차는 $\sigma^2I$라는 상수행렬로 재정의 하였다. 이때 $\sigma^2$의 값은 다음의 값 중 하나를 선택하면 된다.

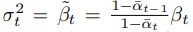
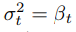
🤔 두 번째 DDPM의 장점
앞서 말한 첫 번째 DDPM과 이어지는 부분인데 우리가 forward process의 매개변수인 $\beta_t$를 상수로 치환하였고, reverse process에서도 마찬가지로 $\sigma_t^2$를 $\beta_t$와 관련된 값으로 변경함으로써 학습과정을 단순화 하였다.

Reverse process loss function

마지막 매개변수인 $\mu_\theta(x_t,t)$를 정의하기에 앞서 reverse process의 loss function인 $L_{t-1}$를 살펴보자. $L_{t-1}$를 실제 $q(x_{t-1}|x_t,x_0)$에서 샐플링한 값과 $**p_\theta(x_{t-1}|x_t)**$에서 샘플링한 값을 사용하여 다음과 같이 재정의 할 수 있다.

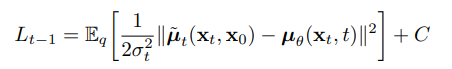
또한 $x_t$를 다음과 같이 재정의 할 수 있다.

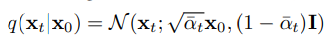
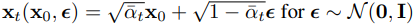
앞서 Diffusion모델을 설명할 때 step별로 $x_T$를 구하는 것이 아니라 한번에 $x_T$를 구하는 공식을 설명하였는데 이를 이용하여 $L_{t-1}$을 재정의 할 수 있다.

🤔 세 번째 DDPM의 장점
기존의 Diffusion 모델에서는 $x_t$를 통해 $x_{t-1}$를 샘플링하지만, DDPM에서는 처음의 noise를residual 로써 활용하여 예측하였다.

4. $\mu_\theta(x_t,t)$

residual을 활용하여 reverse process의 마지막 매개변수인 $\mu_\theta(x_t,t)$는 다음과 같이 정의된다.

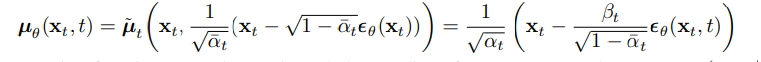
이렇게 해서 $p_\theta(x_{t-1}|x_t)$의 두개의 매개변수 중 첫 번째 매개변수인 분산은 상수행렬로 고정함으로써 구하였고, 두 번째 매개변수인 기대값은 식을 통해 얻어낼 수 있었다. 즉 이렇게 얻은 매개변수를 통해 우리는 $p_\theta(x_{t-1}|x_t)$로 부터 $x_{t-1}$을 샘플링할 수 있다. 샘플링 과정은 다음과 같은 알고리즘으로 표현된다.

이후 Langevin dynamics를 적용하여 최종적인 $L_{t-1}$을 다음과 같이 정의할 수 있다.

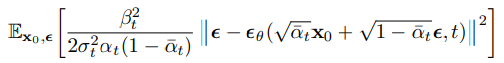
이러한 일련의 과정들을 다음과 같이 알고리즘으로 표현할 수 있다.