Introduction
NeRF 모델은 정말 간단하게 설명하면 2D Image를 통해 3D Real world 형태로 rendering을 진행한 모델이다. 이해를 돕기 위해 사진을 확인해 보자.
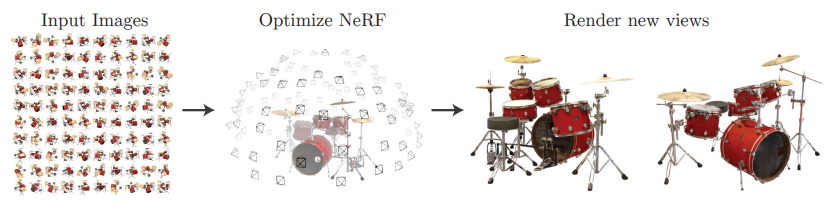
이렇게 다양한 각도에서 찍은 2D Image를 통해 3D Rendered view를 생성해내는 모델이다. 더 자세한 내용은 차차 설명할 예정이다.
Background knowledge
NeRF논문을 리뷰하기 전 NeRF의 원리를 먼저 이해하는 것이 도움이 된다. NeRF는 image plane에서 Real World 3D Rendering view를 생성하는 것이다. 즉 NeRF의 과정은 카메라가 이미지를 추출해 내는 과정의 정확히 반대 과정이다.
🤔 NeRF와 Camera
NeRF: image plane → normalized plane → Real World
Camera: Real World → normalized plane → image plane
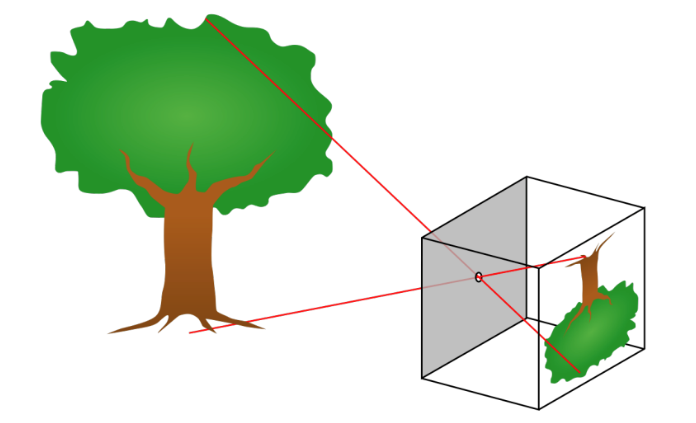
카메라가 어떻게 이미지를 추출하는지 알 수 있다면, 이미지로부터 Real world를 알아내는 NeRF의 과정을 이해할 수 있게 된다. 카메라 내부 파라미터, 외부 파라미터, Ray를 이해해 보자. 카메라 내부 파라미터, 외부 파라미터에 대해 간략하게 설명하자면 다음과 같다.
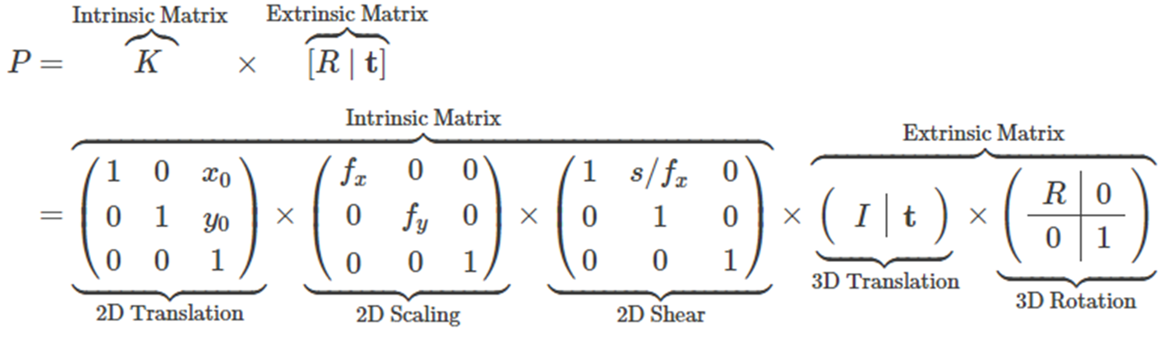
Camera Intrinsic parameters
Camera Intrinsic prameter란 pinhole camera가 Real world에 있는 물체가 어떻게 카메라의 image plane에 맺히는 과정을 설명하는 parameter이다.
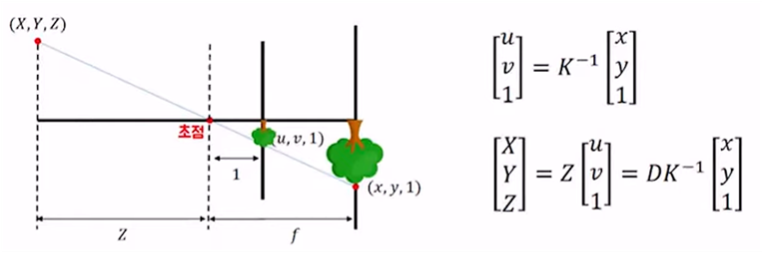
(X,Y,Z)는 Real World상의 좌표이고, (u,v,1)은 normalized plane, (x,y,1)은 image plane을 뜻한다. 여기서 K가 Camera Intrinsic parameter이다. 좌표를 통해 알 수 있듯이 Z축이 3D 입체를 표현하는 축이 된다.
🤔 Normalized plane
Real world의 3D 물체를 image로 표현할 때 거치는 단계가 Normalized plane이다. 이러한 단계가 필요한 이유는 Real world의 3D 물체는 3차원 좌표계로 표현되어 있지만 image는 픽셀로 표현되어 지기 때문에 3차원 좌표계에서 2차원 픽셀 형태로 표현하기 위한 중간 과정을 normalized plane이라고 생각하면 된다.
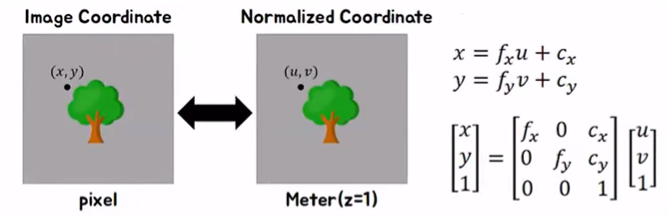
위의 사진에서 확인할 수 있듯이 Camera Intrinsic parameter인 K를 살펴보면 로 구성되어 있는것을 확인할 수 있다. 이 두가지 parameter에 대해 자세히 설명하자면 다음과 같다.
🤔 focal length와 c
focal length인 는 닮은꼴 삼각형을 이용하여 normalized plane에서 image plane으로 transform하는 parameter이다. 이때 c는 와 인데 이는 normalized plane과 image plane의 좌표위치가 상이하여 필요하게된 parameter이다. normalied plane에서는 (0,0)의 좌표가 이미지의 가운데 부분이지만, image plane에서는 (0,0)의 좌표가 이미지의 왼쪽 위 이기 때문에 이러한 c parameter를 사용한다.
🤔 NeRF
NeRF 에서는 image plane에서 normalized plane을 구해야 하기 때문에 camera intrinsic parameter의 matrix인 K의 역행렬을 통해 구할 수 있다.
Camera Extrinsic parameters
Camera Extrinsic parameter란 3D 공간 내에서 카메라가 어디에 위치하고 있고, 어디를 바라보고 있는지에 대한 Parameter입니다. 즉 이러한 Camera Extrinsic parameter는 Real world의 3D 객체를 camera coordinates로 변경해주는 변수이다.
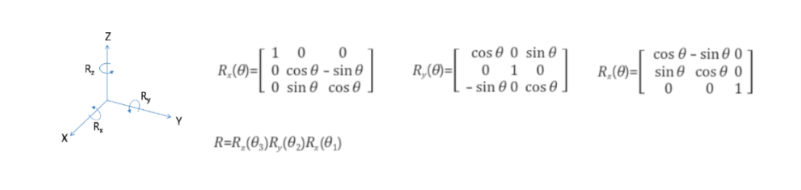
위의 사진은 3D rotation matrix를 구하는 과정이다. 이러한 3D rotation matrix를 통해 다음과 같은 camera coordinates를 구할 수 있다.
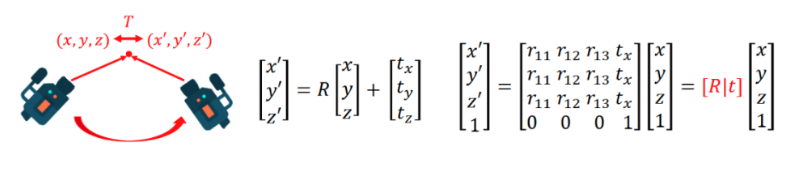
- 더 자세한 수식
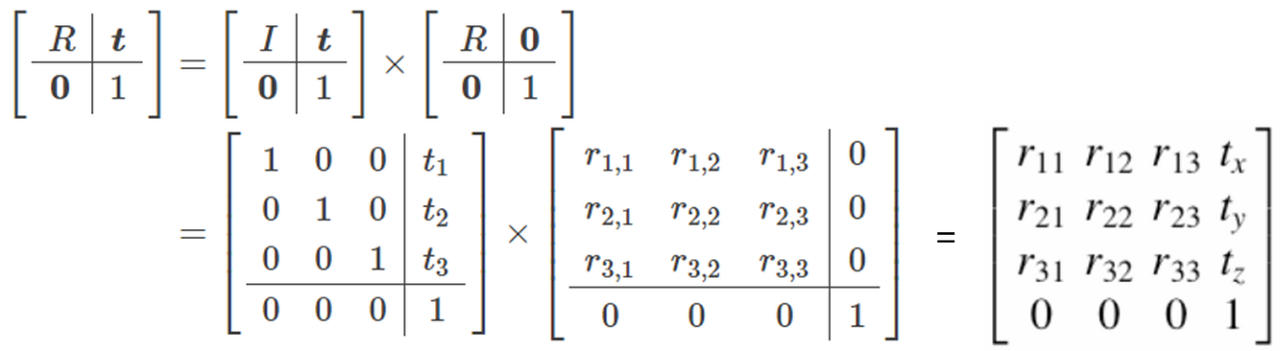
🤔 NeRF
NeRF의 궁극적인 목표는 image plane에서 3D Real world 객체를 표현하는 것이기 때문에 위의 과정의 반대 과정이 필요하다. 이 과정은 camera intrinsic parameter와 마찬가지로 역행렬을 통해 구할 수 있다.
Ray
Ray는 NeRF 논문의 핵심 개념이다. Ray는 이미지의 한 pixel 상에서 3D 객체를 향해 나아가는 방향벡터를 의미한다. Ray의 구성요소를 살펴보면 다음과 같다.
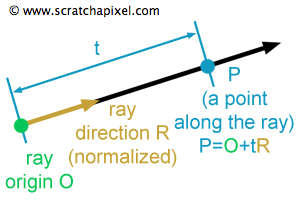
Ray를 수식으로 표현하면 o + td 가 된다. 여기서 t는 방향에 대한 가중치 값들의 합이 되는데 이것이 NeRF에서는 Z 좌표값이 되는 것 이다. Ray가 실제로 NeRF에서 어떠한 원리로 사용되는지 다음의 그림을 통해 확인해 보자.
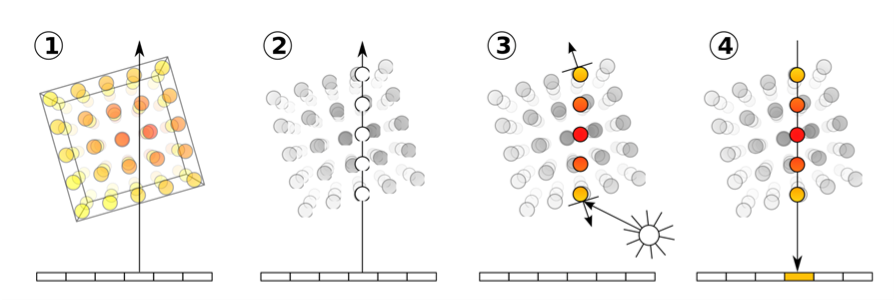
우선 한 이미지의 픽셀에서 객체를 통과하는 Ray를 발사한다. 이후 Ray 위의 임의의 Z축 좌표들을 추출한다. 즉 하나의 픽셀에 여러개의 Z축 좌표가 sampling 되는 것 이다. 이후 각 Z축 지점마다 density와 RGB 값을 구한다. 그런 다음 모든 Z축 지점의 RGB값과 Density의 곱의 합을 구하여 최종적인 RGB를 구하게 되는 것 이다. Ray에 대해 설명하기 위해 NeRF의 과정을 간략하게 설명하였는데 이는 추후 NeRF의 모델 구조에서 자세히 다루도록 하겠다.
Ray를 계산하는 방법은 다음과 같다.
- Normalized plane의 (x,y) 를 구하기 위해 intrinsic parameter를 사용한다.
- Normalized plane에서 extrinsic parameter를 통해 ray direction(ray_d)을 구한다.
- Extrinsic parameter의 translation을 담당했던 t를 통해 ray orientation(ray_o)을 구한다.
NeRF 모델 구조
Introduction
지금까지 확인하였던 Background를 통해 NeRF의 구조를 확인해 보자. 가장 처음에 소개했듯이 NeRF 모델은 N개의 시점에서 찍은 2D image를 임의의 시점에서 찍은 2D image로 변환 후 이를 rendering하여 최종적인 3D rendered된 모델이 output으로 나오게 된다. NeRF 모델의 전체적인 pipeline은 다음과 같다.
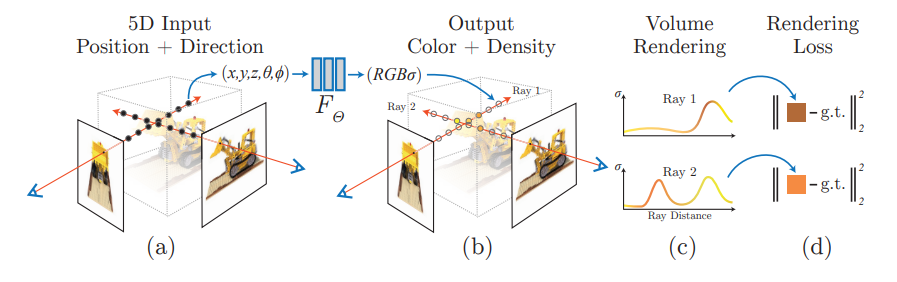
🤔 Neural Radiance Field란?
여러개의 2D image를 통해 3D model로 rendering하는 하나의 방법론 이다. 각 위치 값인 (x,y,z)가 input으로 주어지면 output으로 RGB값을 연산하는 함수의 형태이다. 수식으로 확인하면 다음과 같다.$$F_\theta: (x,d) \rightarrow (c,\sigma)$$ x: input으로 주어지는 이미지의 위치 좌표(x,y,z) d: input으로 주어지는 바라보는 방향(ray_d) c: output으로 나오는 RGB값 $\sigma$: output으로 나오는 density값
Model structure
NeRF 모델의 구조는 MLP로 구성되어 있는 매우 간단한 구조이다.
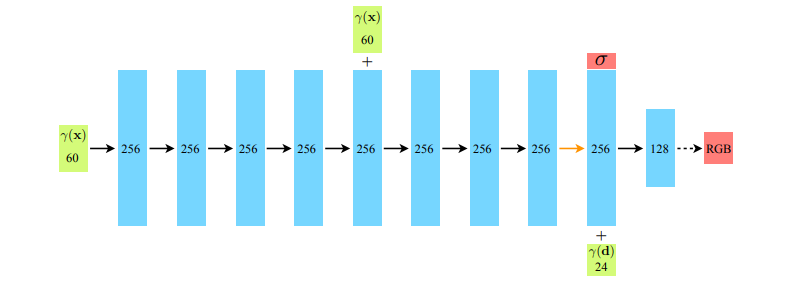
처음에 60차원의 (x,y,z)좌표를 처음 모델의 input으로 받아 MLP layer를 거쳐 중간에 density값을 출력합니다. 이후 direction 정보를 추가로 제공하여 최종적인 RGB 값을 출력하게 된다.
Positional Encoding
처음에 NeRF의 input으로 들어가는 차원이 5차원이고 이중 위치정보인 (x,y,z)는 3차원인데 왜 모델의 구조에서는 60차원인지 의문일 것 이다. 이는 하나의 trick인 positional embedding을 사용하여 차원의 수를 늘렸기 때문이다. 적은 차원의 수는 많은 정보를 포함하고 있지 않기 때문에 이를 해결하기 위해 다음과 같은 방법으로 차원의 수를 늘렸다.
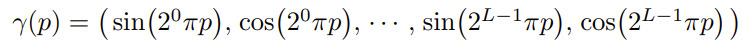
만약 L=10 이라면, (x,y,z)는 각각 20차원이 되고 총 60차원이 되는 것이다.
🤔 NeRF의 positional encoding
연속적인 입력 데이터의 좌표들을 좀 더 고차원 데이터로 매핑해 MLP가 좀더 쉽게 고차원 성분, 즉 scene에 있는 테두리들을 좀 더 쉽게 근사할 수 있게 만들기 위해 사용된다.
Volume Rendering
지금까지는 NeRF가 어떻게 RGB값과 density값을 얻어내는 과정을 확인하였다. 그렇다면 실제로 어떠한 방식으로 RGB값이 선정되는지 그 자세한 과정을 살펴보도록 하자. 이전에 Ray를 설명할 때 간단하게 언급했던 개념을 다시 확인한다면 이해하는데 많은 도움이 된다.
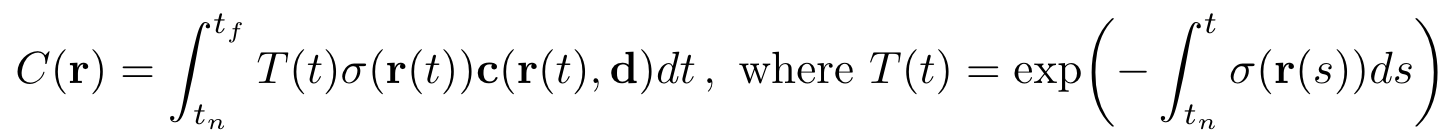
위의 수식에서 density값인 와 RGB값인 는 이전에 MLP 레이어를 통해 얻어진 값이다. 즉 위의 수식이 의미하는 바는 한 특정 픽셀에서 추출한 모든 Z축 위의 점(ray에서의 t)들의 와 를 계산하여 최종적인 컬러 output인 을 얻게 되는 것 이다.
여기서 중요한 term은 바로 이다. 는 ray의 앞쪽에 있는 물체의 density 를 고려하여 최종적인 RGB값을 선택하는데 영향을 주는 parameter이다. 다음의 그림을 통해 확인해 보자.
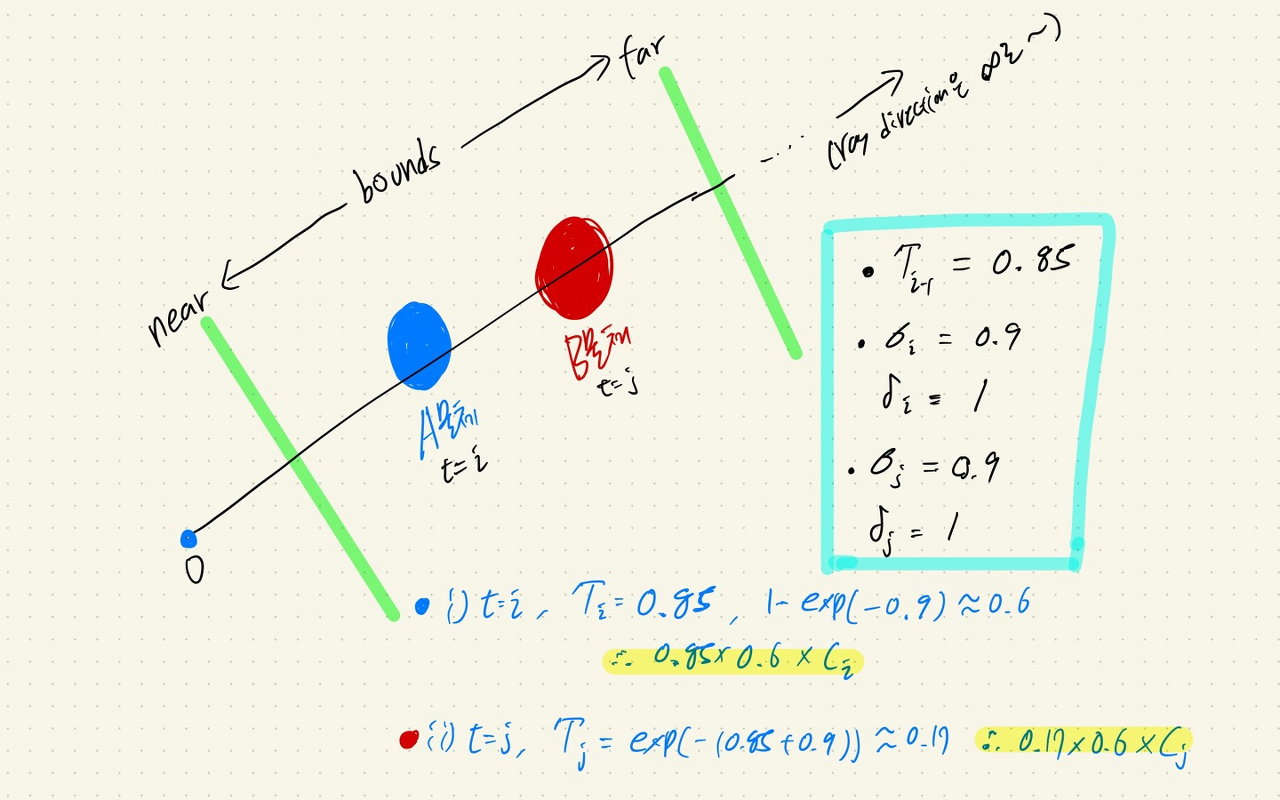
출처: https://kyujinpy.tistory.com/16
이처럼 A물체의 density값이 높다면 B물체의 density값이 아무리 높아도 B물체의 최종적인 RGB값의 가중치는 A물체의 RGB가중치 보다 작아지게 되는 것 이다. 즉 밀도가 아무리 높은 B물체가 존재하더라도 앞에 밀도가 적당히 높은 A물체가 존재하게 되면 B물체의 RGB 가중치는 상대적으로 낮아지게 되는 구조를 가지게 된다.
stratified sampling approach
위에서 구한 Volume rendering의 수식은 continuous한 상태를 표현한 식이다. 하지만 실제 이미지는 continuous하지 않고 discrete하게 표현되기 때문에 이에 맞춰 수식을 표현하면 다음과 같아진다.
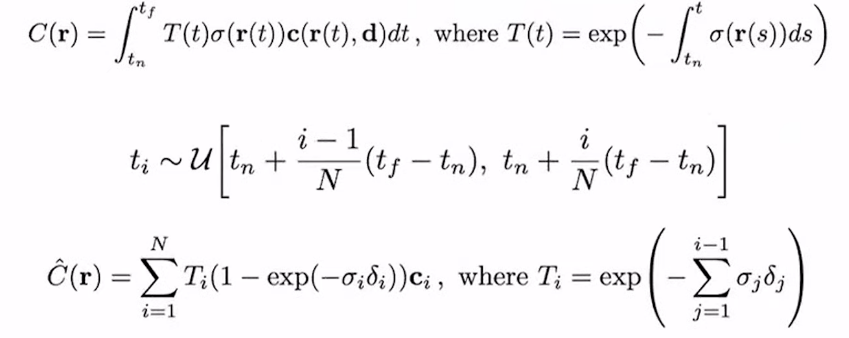
여기서 은 기존의 과는 다르게 discrete하게 표현되어 있다. 차이점은 바로 인데 이는 discrete하게 표현하기 위한 변수로써 들 사이의 거리를 뜻한다.
🤔 의 exp 함수
를 살펴보면 부분을 확인할 수 있다. 갑자기 나온 부분이라 의아하였지만 이는 아래의 논문을 참고하여 사용한 식이다. 아래의 논문은 continuous한 식을 프로그래밍의 용이성을 위해 discrete하게 바꾸는 방법을 제시한 논문이다.
Max, N.: Optical models for direct volume rendering. IEEE Transactions on Visualization and Computer Graphics (1995)
Hierarchical volume sampling
NeRF는 원래 ray에서 N개의 포인트를 뽑아 렌더링에 사용하려고 했지만 이는 객체 뿐만 아니라 아무것도 없는 빈 공간도 추출하게 되어 비효율적이였다. 따라서 이를 해결하고자 Hierarchical volume sampling 방법을 도입하게 되었다. Hierarchical volume sampling 이란 두 가지의 네트워크를 사용하여 비효율성을 줄인 방법이다.
-
Coarse Network
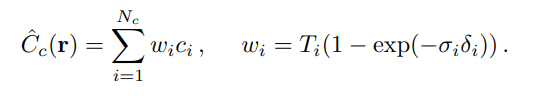
Coarse network는 가장 기본적인 NeRF이다. 위에서 확인했던 Volume rendering의 수식과 동일하다. 차이점은 N개의 데이터를 바로 샘플링하는 것이 아닌 개만을 샘플링한다. 이후 Coarse network를 학습을 시킨 후 이를 통해 얻은 의 분포를 통해 추가적으로 개를 샘플링한다.
-
Fine Network
총 + 개의 샘플을 이용하여 Fine network를 학습시킨다.
Model loss function
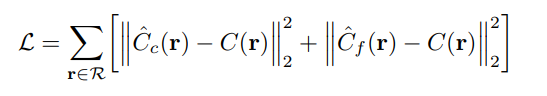
최종적으로 RGB값에 대한 차이를 통해 MSE를 계산하게 되는데 각각의 데트워크 에 대한 loss를 계산하여 이를 합한 형태가 NeRF 모델의 Loss function 이다.