Introduction

GAN 이란?

GAN(Generative Adversarial Nets)

GAN 모델은 이미지를 생성해 내는 모델로써 2014년에 등장했다. 이후 현재까지 GAN을 기반으로한 수많은 발전된 모델들이 파생되었다. 이미지 생성이란, 기존의 있던 데이터를 기반으로 그럴싸한 이미지를 생성해 낸다는 뜻이다. 즉, 주어진 이미지 데이터 내에서 특정한 이미지를 추출해 내는 classification 문제가 아닌 새로운 있을법한 이미지를 만들어 내는 것이 특징이다.

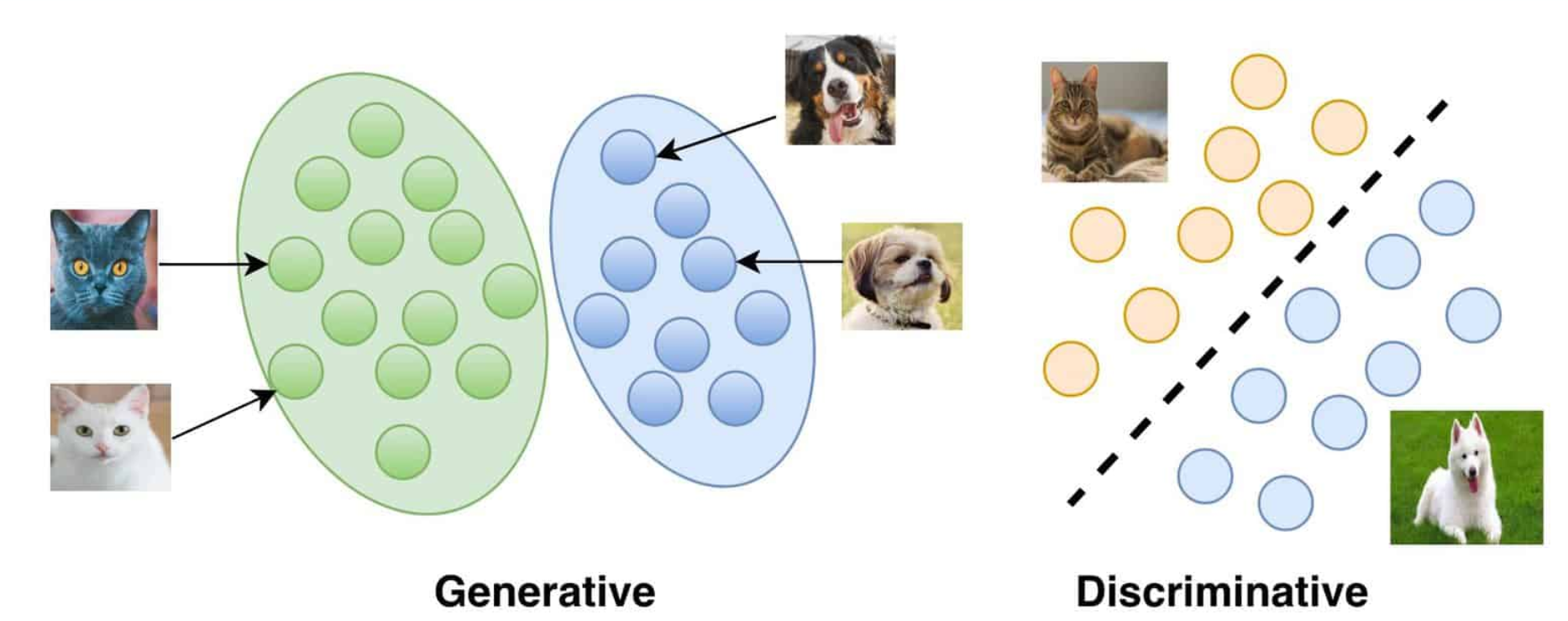
GAN의 등장배경

GAN 모델이 나오기 이전 배경을 살펴보면, 딥러닝 모델들은 엄청난 발전이 이루어 졌다. 특히 dicriminative model들은 고차원의 풍부한 데이터들을 mapping할 수 있는 딥러닝의 특성을 잘 활용하여 발전하게 되었다. 하지만 generative 모델들은 dicriminative 모델들에 비해서 발전이 더디었는데, 그 이유는 maximum likelihood estimation으로 부터 파생되는 다루기 힘든 수많은 확률론적 계산들을 처리함에 있어 어려움이 있어서 이다. 하지만 GAN 모델은 이러한 difficulty를 피해가는 방법을 제시하였다. 즉 다시말해 GAN 모델은 복잡한 Markov chain 또는 network에 대한 대략적인 추론 없이 오로지 딥러닝의 backpropagation을 통해 모델을 train 할 수 있고, 이미지를 생성해 낼 수 있다.

GAN 모델의 특징

Adversarial nets

GAN 모델의 이름에서도 알 수 있듯이 Adversarial nets이 GAN의 가장 핵심적인 특징이다. 이전에 GAN의 등장배경에서 말했던 generative 모델의 difficulty를 해결하는 방법으로 나온 것이 바로 Adversarial nets이다. Adversarial nets은 다음과 같은 두 가지 모델로 구성되어 있다. Adversarial nets에 관한 자세한 내용은 아래에 기술해 두었다.

💡
1. Discriminator: 해당 sample이 generated model distribution에서 왔는지, 혹은 data distribution 에서 왔는지 판별하는 모델
2. Generator: 그럴싸한 이미지 확률 분포를 만들어 내는 모델

framework

이러한 두개의 모델이 서로 경쟁하며 모델을 발전시키는 형태이다. 즉 다시말해, 일종의 minmax two-player game인 것이다. generator는 최대한 그럴싸한 이미지를 생성하도록 학습되고, discriminator는 최대한 실제 이미지 데이터와 가짜 이미지 데이터를 잘 구분하도록 학습된다.

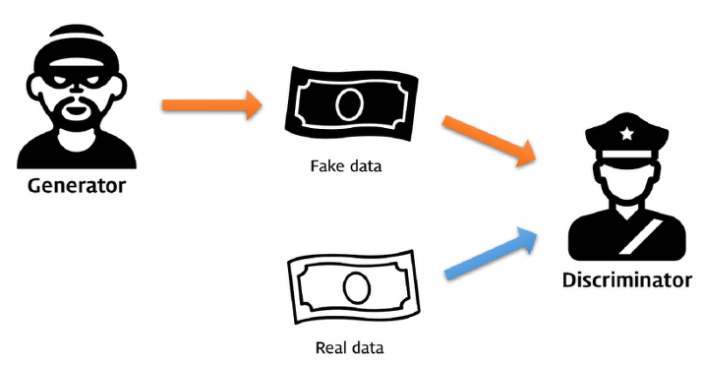
☝ 여기서 기억해야 할 점은 Generator 모델의 ouput은 확률분포 형태이다. 즉, Generator 모델은 원래의 original data의 확률분포와 유사하게 만드는 것이 최종 목표이다.

Adversarial nets

Adversarial nets의 구성

앞서 언급한 것 처럼 Adversarial nets는 generator 와 discriminator로 구성되어 있다.

💡
1. Generator model $G(z;\theta_z)$
2. Discriminator model $D(x;\theta_d$)

Adversarial nets의 과정

two-player minimax game을 진행하는 GAN의 목점함수를 살펴보면 Adversarial nets의 전체적인 과정을 대략적을 알 수 있다.

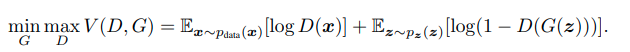
G는 목적함수 V를 낮추고자 하고, D는 목적함수 V를 높이고자 노력한다. D는 0~1사이의 스칼라 값을 출력으로 하는데 1에 가까울 수록 실제 데이터와 가깝다는 뜻이고 0에 가까울 수록 생성된 가짜 데이터 라는 뜻이다.

Discriminator의 학습 과정

왼쪽에 있는 식은 원본 데이터 분포로 부터 x를 샘플링한 뒤 이를 Discriminator에 통과시켜 이것이 실제 원본 데이터분포 에서 온 값인지, 아니면 가짜인지 판별하게 된다. 즉 다시 말해, 왼쪽식은 원본 데이터에 대해서는 1로 학습이 되어 좌측에 있는 식을 최대화 시킨다.

이와 반대로 우측에 있는 식은 noise가 포함된 분포로 부터 생성된 G(z)를 Discriminator에 통과시켜 이것이 만들어진 가짜 이미지인지 를 판별하게 된다. 즉, 오른쪽 식은 생성된 가짜 데이터에 대해서는 0이 되게끔 학습되어 최종적으로 우측에 있는 식을 최대화 시킨다.

Generator의 학습 과정

Generator의 경우 우변에서만 존재하는데, Generator는 최대한 Discriminator에게 실제 데이터로써 판별되기 위해 노력한다. 목적함수를 최대한 줄이려는 Generator는 우변에서 $D(G(z))$ 출력값이 1이 되도록 만드는 것이 Generator의 역할이 된다.

Adversarial nets의 목표

이렇게 Adversarial nets를 거쳐 최종적으로 원하는 목표는 총 2가지 이다.

1. $P_g$ → $P_{data}$
2. $D(G(z)) = 0.5$

첫번째는 Generator가 생성해낸 데이터의 분포가 원래의 데이터 분포와 일치하게 되는 것이고, 두번째는 Discriminator가 원본의 이미지와 생성된 가짜 이미지를 구분할 수 없는 상태가 되는 것이 목표이다.

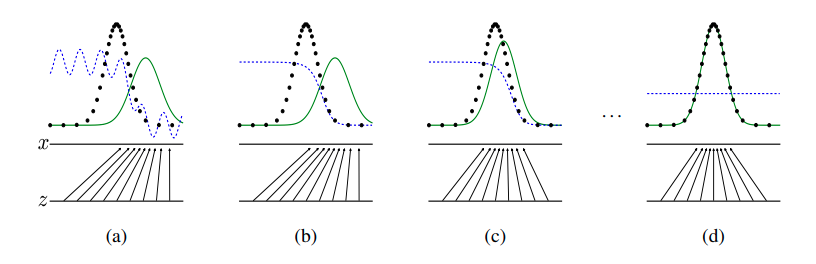
검은색 점선: 원본 데이터의 분포
초록색 선: Generator의 분포
파란색 점선: Discriminator의 분포

위의 그림을 살펴보면 학습이 진행될 수록 Generator의 분포가 원본 데이터의 분포와 유사해 지는 것을 확인할 수 있다. 처음에는 원본 데이터와 Generator의 분포를 Discriminator가 잘 구분을 하였지만 Generator의 분포가 원본데이터의 분포와 유사해 질수록 Discriminator가 두개를 잘 구분하지 못하게 된다.

☝ 즉 GAN 논문에서 주장하는 바는 minimax 이론을 적용한 목적함수 V(D,G)가 Generator의 분포를 원본 데이터의 분포와 유사하게 만든다는 것 이다. 그렇다면 실제로 Generator의 분포가 원본데이터의 분포와 유사해 지는지 수식을 통해 알아보도록 하자

Theoretical Results

앞서 말했듯이, 어떠한 수학적인 근거를 바탕으로 $p_g$ 가 $p_{data}$ 유사해 지는지 살펴보도록 하자.

Global Optima point

우선 Discriminator가 어떠한 point에서 Global optima를 갖게 되는지 알아보자.

proposition

Generator가 fixed 되어 있을 때, Discriminator의 optimal 값은 다음과 같다.

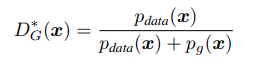
proof

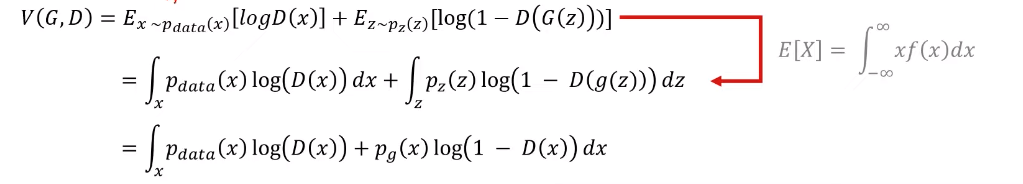
첫 번째 식에서 E[X]는 xf(x)를 적분한 것과 같으므로 두 번째 식이 완성된다. 두 번째 식에서 세 번째 식이 도출된 이유는 x가 z 도메인에서 매핑되었기 때문이다.

최종적인 식을 보면 $alog(y) + blog(1-y)$ 형태 이다. 이를 그래프를 그려 확인해보면

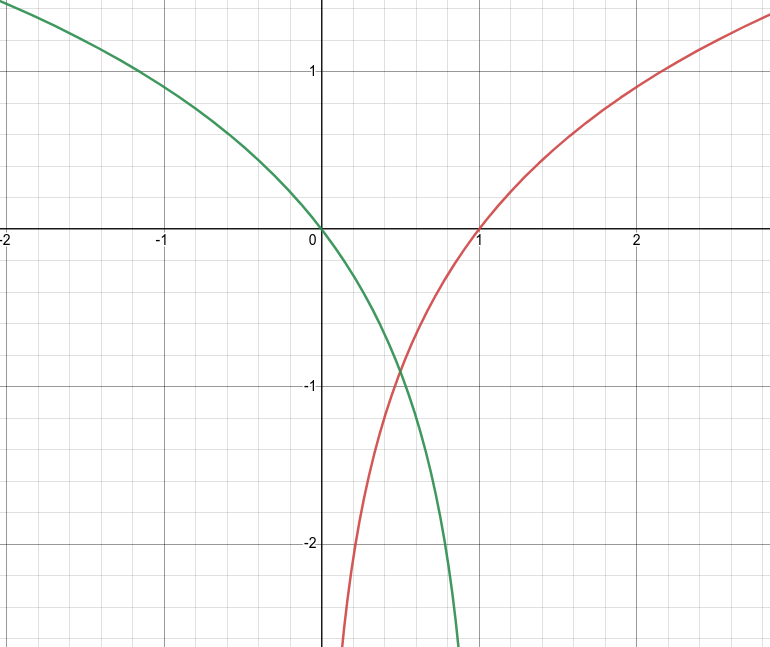
이렇게 $\frac {a}{a+b}$ 에서 $alog(y) + blog(1-y)$ 가 최대값을 가진다는 것을 알 수 있다. 이러한 과정은 단순한 미분과정을 통해서도 확인할 수 있다.

따라서 Generator가 fixed 되어있을 때, Discriminator의 optimal 값은 아래와 같음을 증명할 수 있다.

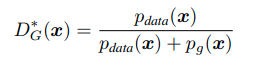
Global Optimality of $p_g = p_{data}$

어떠한 point에서 Discriminator가 global optima를 갖게 된다는 것을 알았으니, 이번에는 실제로 Generator의 global optima가 $p_g = p_{data}$ 인지 확인하는 과정이다.

proof

우선 별도의 함수 C(G)위와 같이 정의한다. 이후 이전에 구했던 Discriminator의 optimal point를 대입하여 2번째 식을 얻어낼 수 있다. 이후 좌변과 우변에 log2씩을 더한뒤 마지막에 log4를 빼주는데 이는 추후에 사용될 JSD (Jenson-Shannon divergence)를 적용하기 위한 편의상 목적으로 진행 된 것 이다. 이후 KL divergence과 JSD (Jenson-Shannon divergence)를 적용하여 최종적인 식이 나오게 된 것 이다.

여기서 KL divergence와 JSD를 간단히 설명하자면 KL divergence는 cross entropy에서 entropy를 뺀 것이며, 확률분포 P와 Q 사이의 asymmetric한 차이를 의미한다. JSD는 KL divergence를 두번구해 평균을 낸 것이며, 두 확률분포 P와 Q 사이의 distance 를 의미한다.

이렇게 최종적으로 나온 식이 의미하는 바는 다음과 같다.

☝ 즉, $p_g$ 와 $p_{data}$ 의 분포가 유사할 수록 마지막 식의 값은 최소값인 -log4와 가까워 진다. 따라서 global optima를 얻을 수 있는 유일한 방법은 $p_g$ 와 $p_{data}$ 가 일치해야 하기 때문에 목적함수는 $p_g$ 와 $p_{data}$ 를 유사하게 만드는 쪽으로 학습이 진행된다는 것을 증명한다.