유기기전력과 회전력
자속 ϕf가 형성되어 있는 공간 내에 각속도 θm˙으로 회전하는 회전하는 직류 전동기의 유기 기전력.
(ke는 역기전력 상수)
자속 ϕf가 형성되어 있는 공간 내에 전류 ia가 흐르는 직류 전동기의 회전력.
(kT는 토크 상수)
에너지 보존
일률 P는 서로 같아야한다.
Pe=eaia=keϕfθm˙iaPm=Tmθm˙=kTϕfiaθm˙
keϕf=Ke,kTϕf=KT 라고 할때 Ke=KT.
모터의 전기 방정식

DC Motor의 등가회로 (전류는 ia)
등가회로에 KVL 적용
va=Raia+Ladtdia+ea (ea는 유기 기전력)
va=Raia+Ladtdia+Keθm˙
모터의 기계 방정식
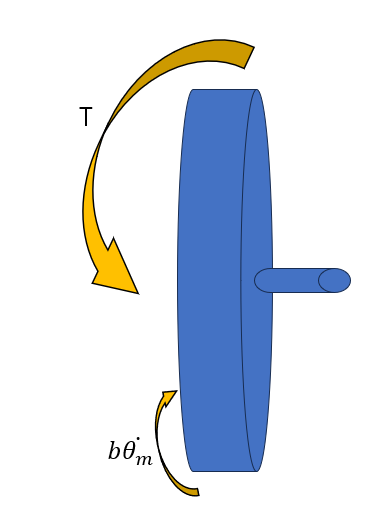
∑T=Jθm¨
Te−bθm˙=Jθm¨ (Tm=KTia, b: 마찰계수)
Te=Jθm¨+bθm˙
전기방정식과 기계방정식의 라플라스변환
Va(s)=RaIa(s)+La(sIa(s)−Ia(0))+Keθm˙(s), (Ia(0)=0이라고 가정)
Ia(s)=Las+RaVa(s)−Keθm˙
KTIa(s)=J(sθm˙(s)−θm˙(0))+bθm˙(s), (θm˙(0)=0이라고 가정)
θm˙(s)=Js+bKTIa(s)
위 식을 아래에 대입하여 정리하면 모터의 입력 Va(s)과 출력 θm˙(s)에 대한 전달함수를 구할 수 있고, 다음과 같다.
Va(s)θm˙(s)=(Las+Ra)(Js+b)+KeKTKT
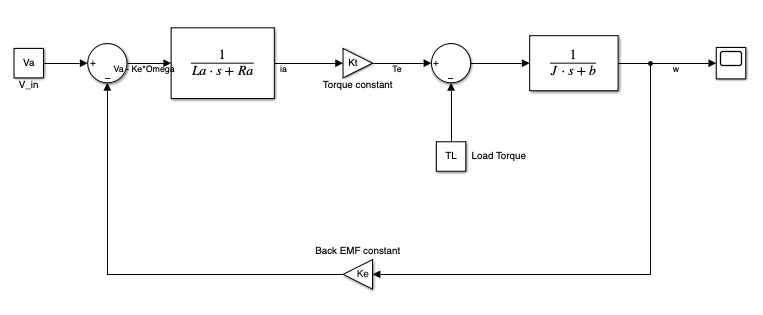
DC 모터의 블록선도
b=τJ
τ: 시정수
시정수
- 정상상태의 63.2%에 도달할 때 까지의 시간



