Algorithm
입력 : 포인트클라우드 쌍 (P, Q), (P: 모델, Q: 가진 데이터)
출력 : Q를 P로 정렬하는 transformation T
1. P와 Q의 모든점에 대해 normal vector {n_p}, {n_q} 계산;
2. FPFH 특징 계산 F(P), F(Q);
3. K_I, K_II;
4. K_III;
5. T = I, mu = D^2;
while mu > delta^2 do
Jr = 0, r = 0;
for (p, q) in K_III do
6. l_(p,q) 계산;
7. Jr, r 업데이트;
end for
8. T 업데이트;
4 iteration 마다 mu = mu/2;
end while
Output T5. T, μ \mu μ
T T T I I I μ \mu μ
6. l p , q l_{p, q} l p , q
Gauss-Newton Method
Least Square
최소 제곱법(Least Square)은 훈련 샘플 ( x i , y i ) (x_i, y_i) ( x i , y i )
E ( p ) = ∑ i = 1 N ∣ ∣ r i ( p ) ∣ ∣ 2 , r i ( p ) = y i − f ( x i , p ) E(p) = \sum_{i=1}^N ||r_i(p)||^2, \ r_i(p)=y_i-f(x_i, p) E ( p ) = i = 1 ∑ N ∣ ∣ r i ( p ) ∣ ∣ 2 , r i ( p ) = y i − f ( x i , p ) Least Square에서는 E의 최소를 찾아야하기 때문에 ∂ E ( p ) ∂ p = 0 \frac{\partial E(p)}{\partial p}=0 ∂ p ∂ E ( p ) = 0
Line Process
Line Process 는 노이즈가 낀 3D 포인트 클라우드 데이터에서 물체의 표면을 추정할 때 사용한다.
불연속적 구간을 고려하는 추정을 위한 방법이다.
정답을 u u u d d d
E ( u ) = ∑ s ∈ S ( ( u s − d s ) 2 + λ ∑ t ∈ N ( s ) ( u s − u t ) 2 ) E(u) = \sum_{s \in S}((u_s-d_s)^2 + \lambda \sum_{t \in N(s)} (u_s - u_t)^2) E ( u ) = s ∈ S ∑ ( ( u s − d s ) 2 + λ t ∈ N ( s ) ∑ ( u s − u t ) 2 ) E E E u u u
( u s − d s ) 2 (u_s-d_s)^2 ( u s − d s ) 2
∑ t ∈ N ( s ) ( u s − u t ) 2 \sum_{t \in N(s)} (u_s - u_t)^2 ∑ t ∈ N ( s ) ( u s − u t ) 2 u s u_s u s u t u_t u t u s u_s u s
이렇게 계산하면 그림에서의 c처럼 불연속 구간이 무너지게 된다.
이를 해결하기 위해 Line Process가 사용된다.
Line process를 포함해서 Error를 다시 써보면
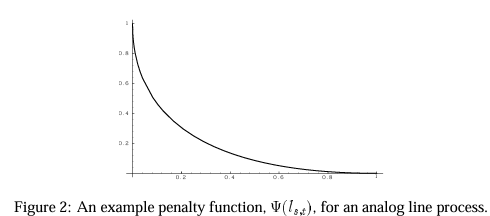
E ( u , L ) = ∑ s ∈ S ( ( u s − d s ) 2 + λ ∑ t ∈ N ( s ) ( ( u s − u t ) 2 l s , t + ψ ( l s , t ) ) ) E(u, L) = \sum_{s \in S}((u_s-d_s)^2 + \lambda \sum_{t \in N(s)} ((u_s - u_t)^2l_{s,t}+\psi (l_{s,t}))) E ( u , L ) = s ∈ S ∑ ( ( u s − d s ) 2 + λ t ∈ N ( s ) ∑ ( ( u s − u t ) 2 l s , t + ψ ( l s , t ) ) ) l s , t ∈ L l_{s,t} \in L l s , t ∈ L l s , t l_{s,t} l s , t
l s , t l_{s,t} l s , t u s u_s u s
ψ ( z ) = ( z − 1 ) 2 \psi(z)=(\sqrt z - 1)^2 ψ ( z ) = ( z − 1 ) 2
ICP (Iterative Closest Point)
ICP는 두 클라우드 포인트 사이의 차이를 최소화 시키는 알고리즘이다.
K I I I K_{III} K I I I P P P Q Q Q P P P Q Q Q
P = T Q P = TQ P = T Q
하지만 초기 위치가 너무 멀리 떨어져 있다면 Error가 너무 커지게 되고, ICP를 진행하는 동안 local Minimum에 빠질 수 있다는 문제가 생긴다.
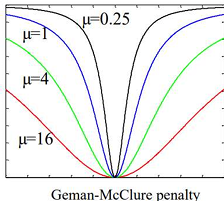
따라서 residual(잔차)를 제곱하는 것이 아닌 Geman-McClure penalty 함수를 이용한다.
μ \mu μ μ \mu μ
Geman-McClure penalty를 ρ ( x ) = μ x 2 μ + x 2 \rho(x) = \frac{\mu x^2}{\mu + x^2} ρ ( x ) = μ + x 2 μ x 2
E ( T ) = ∑ ( p , q ) ∈ K ρ ( ∣ ∣ p − T q ∣ ∣ ) E(T) = \sum_{(p, q) \in K} \rho(||p-Tq||) E ( T ) = ( p , q ) ∈ K ∑ ρ ( ∣ ∣ p − T q ∣ ∣ ) 이렇게 사용하면 최소 제곱법의 문제를 해결할 수 있지만 풀기 어려워진다.
그래서 여기에 Line Process를 적용한다.
E ( T , L ) = ∑ ( p , q ) ∈ K l p , q ∣ ∣ p − T q ∣ ∣ 2 + ∑ ( p , q ) ∈ K ψ ( l p , q ) E(T, L) = \sum_{(p, q) \in K} l_{p,q}||p-Tq||^2+\sum_{(p, q) \in K}\psi(l_{p,q}) E ( T , L ) = ( p , q ) ∈ K ∑ l p , q ∣ ∣ p − T q ∣ ∣ 2 + ( p , q ) ∈ K ∑ ψ ( l p , q ) ψ ( l p , q ) = μ ( l p , q − 1 ) 2 \psi(l_{p,q})=\mu(\sqrt{l_{p,q}}-1)^2 ψ ( l p , q ) = μ ( l p , q − 1 ) 2
∂ E ∂ l p , q = ∣ ∣ p − T q ∣ ∣ 2 + μ l p , q − 1 l p , q = 0 → l p , q = ( μ μ + ∣ ∣ p − T q ∣ ∣ 2 ) 2 \frac{\partial E}{\partial l_{p,q}} = ||p-Tq||^2 + \mu \frac{\sqrt{l_{p,q}} -1}{\sqrt{l_{p,q}}} = 0 \rightarrow l_{p,q}=(\frac{\mu}{\mu+||p-Tq||^2})^2 ∂ l p , q ∂ E = ∣ ∣ p − T q ∣ ∣ 2 + μ l p , q l p , q − 1 = 0 → l p , q = ( μ + ∣ ∣ p − T q ∣ ∣ 2 μ ) 2
으로 l p , q l_{p,q} l p , q
7. J r , r J_r, r J r , r
r r r r r r
J r J_r J r 한 프레임 사이의 회전은
R t = δ R t ⋅ R t − 1 R_t = \delta R_t \cdot R_{t-1} R t = δ R t ⋅ R t − 1 δ R t ≈ [ 1 − γ β γ 1 − α − β α 1 ] \delta R_t \approx \begin{bmatrix} 1 & - \gamma & \beta\\ \gamma & 1 & -\alpha\\ -\beta & \alpha & 1 \end{bmatrix} δ R t ≈ ⎣ ⎢ ⎡ 1 γ − β − γ 1 α β − α 1 ⎦ ⎥ ⎤ 변환 행렬은
T t = δ T t ⋅ T t − 1 T_t = \delta T_t \cdot T_{t-1} T t = δ T t ⋅ T t − 1 δ T t ≈ [ 1 − γ β a γ 1 − α b − β α 1 c 0 0 0 1 ] \delta T_t \approx \begin{bmatrix} 1 & - \gamma & \beta & a\\ \gamma & 1 & -\alpha & b\\ -\beta & \alpha & 1 & c\\ 0&0&0&1 \end{bmatrix} δ T t ≈ ⎣ ⎢ ⎢ ⎢ ⎡ 1 γ − β 0 − γ 1 α 0 β − α 1 0 a b c 1 ⎦ ⎥ ⎥ ⎥ ⎤ ξ = ( α , β , γ , a , b , c ) T \xi=(\alpha, \beta,\gamma, a,b,c)^T ξ = ( α , β , γ , a , b , c ) T 자코비안 계산
자코비안은 r r r ξ \xi ξ
T = δ T ⋅ T o l d T = \delta T\cdot T_{old} T = δ T ⋅ T o l d
r i ( ξ ) = p i − δ T ⋅ T o l d q i r_i(\xi) = p_i - \delta T\cdot T_{old}q_i r i ( ξ ) = p i − δ T ⋅ T o l d q i J r = ( ∂ r ∂ α … ∂ r ∂ c ) J_r = (\frac{\partial r}{\partial \alpha}\dots \frac{\partial r}{\partial c}) J r = ( ∂ α ∂ r … ∂ c ∂ r ) 8. T 업데이트
Gauss-Newton Method
Gauss-Newton Method는 최소 제곱법에서의 Hessian을 피하기 위해 테일러 전개를 통한 근사로 문제를 풀게 된다.
테일러 전개에 의해
r ( p t + 1 ) ≈ r ( p t ) + J r ( p t ) ( p t + 1 − p t ) r(p_{t+1}) \approx r(p_t)+J_r(p_t)(p_{t+1}-p_t) r ( p t + 1 ) ≈ r ( p t ) + J r ( p t ) ( p t + 1 − p t ) 이 식을 최소 제곱법에서의 Cost function에 대입하면
E ( p t + 1 ) = ∑ i = 1 N ∣ ∣ r i ( p t ) + J r i ( p t ) ( p t + 1 − p t ) ∣ ∣ 2 E(p_{t+1})=\sum_{i=1}^N ||r_i(p_t)+J_{r_i}(p_t)(p_{t+1}-p_t)||^2 E ( p t + 1 ) = i = 1 ∑ N ∣ ∣ r i ( p t ) + J r i ( p t ) ( p t + 1 − p t ) ∣ ∣ 2 ∂ E ∂ p t + 1 = 0 \frac{\partial E}{\partial p_{t+1}}=0 ∂ p t + 1 ∂ E = 0
p t + 1 = p t − ( ∑ i J r i T J r i ) − 1 ∑ i J r i T r i p_{t+1}=p_t-(\sum_iJ_{r_i}^TJ_{r_i})^{-1}\sum_iJ_{r_i}^Tr_i p t + 1 = p t − ( i ∑ J r i T J r i ) − 1 i ∑ J r i T r i 가중치가 있는 최소제곱 문제
E ( p ) = W ∣ ∣ y − A p ∣ ∣ 2 E(p) = W||y-Ap||^2 E ( p ) = W ∣ ∣ y − A p ∣ ∣ 2 위와 같이 최소제곱 문제에 가중치가 붙으면
∂ E ∂ p = − 2 ( y − A p ) T W A = 0 \frac{\partial E}{\partial p} = -2(y-Ap)^TWA=0 ∂ p ∂ E = − 2 ( y − A p ) T W A = 0
p = ( A T W A ) − 1 A T W y p = (A^TWA)^{-1}A^TWy p = ( A T W A ) − 1 A T W y 가 된다.
ξ \xi ξ 라인 프로세스를 포함하는 에러는 가중치가 있는 최소 제곱법 문제이므로
ξ = − ( ∑ i J r i T J r i l p , q ) − 1 ∑ i J r i T l p , q r i \xi=-(\sum_iJ_{r_i}^TJ_{r_i}l_{p,q})^{-1}\sum_iJ_{r_i}^Tl_{p,q}r_i ξ = − ( i ∑ J r i T J r i l p , q ) − 1 i ∑ J r i T l p , q r i 로 업데이트 할 수 있다.
T 업데이트
업데이트 된 ξ \xi ξ
T = δ T ( ξ ) ⋅ T T = \delta T(\xi)\cdot T T = δ T ( ξ ) ⋅ T