센서로부터 센싱한 포인트 클라우드 데이터가 있고, 원하는 물체의 모델 데이터가 있을 때, 포인트 클라우드 데이터로 부터 물체의 위치, 방향을 찾는 과정.

Algorithm

입력: 포인트클라우드 쌍 (P, Q), (P: 모델, Q: 가진 데이터)

출력: Q를 P로 정렬하는 transformation T

1. P와 Q의 모든점에 대해 normal vector {n_p}, {n_q} 계산;
2. FPFH 특징 계산 F(P), F(Q);
3. K_I, K_II;
4. K_III;
5. T = I, mu = D^2;

while mu > delta^2 do
    Jr = 0, r = 0;

    for (p, q) in K_III do
        l_(p,q) 계산;
        Jr, r 업데이트;
    end for

    T 업데이트;
    4 iteration 마다 mu = mu/2;
end while

Output T

1. Normal vector 계산

P와 Q에 존재하는 모든 점에 대해 normal vector를 계산한다.

1) 특정 점과 그 주변점의 공분산 행렬을 만듦.
2) 공분산행렬에 SVD를 적용.
3) normal vector는 가장 작은 고유값에 대응되는 고유벡터.

어떤 점과 그 주변 점들의 집합의 주축을 a,b,c라고 하면, $XX^T$의 eigen value는 $\lambda_1(=a^2), \lambda_2(=b^2), \lambda_3(=c^2)$.

2. Fast Point Feature Histogram (FPFH)

1) 한 점 $p_s$와 이웃한 점 $p_t$를 가지고 Darboux frame을 정의한다.

$\begin{cases} u = n_s\\ v = u\times\frac{(p_t-p_s)}{||p_t-p_s||}\\ w = u\times v \end{cases}$

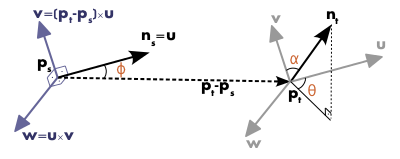
2) Darboux frame이 정의되고 나면, 두 점 $p_s$와 $p_t$의 normal vector의 차이를 가지고 세 가지 feature를 만들게 된다.

$\begin{cases} \alpha = v\cdot n_t\\ \phi = u\cdot\frac{(p_t-p_s)}{||p_t-p_s||}\\ \theta = atan2(w\cdot n_t, u\cdot n_t) \end{cases}$

3) SPFH (Simple Point Feature Histogram) 계산

Qtm[*] 은 Quantum number로 Qtm이 5라면 bin을 5로하여 히스토그램을 생성한다.
각도를 5개 구간으로 나누어 [0~71:1, 72~143:2, ... , 288~359: 5] 히스토그램을 만드는 것.

5로 했을때는 각 각도에 대한 히스토그램이 5차원 데이터로 만들어지기 때문에, SPFH는 15차원이 된다.

4) FPFH 계산

$T$: $p_s$의 이웃점 개수

$w_t$: $p_s$와 $p_t$ 사이의 거리

3. $K_I, K_{II}$

K1

K-d tree를 이용해 각 $p \in P$에 대해 FPFH(Q) 중에 FPFH(p)와 가까운 feature들을 찾고, 각 $q \in Q$에 대해서도 FPFH(P) 중에 FPFH(q)와 가까운 feature들을 찾아서 (p, q) 쌍들을 $K_I$에 저장해둔다.

K2

$K_I$에서 선택된 (p,q) 쌍들로 부터 F(p)의 가장 가까운 피처가 F(q)이고, F(q)의 가장 가까운 피처가 F(p)인 쌍들만 선택하여 $K_{II}$에 저장.

4. $K_{III}$

$K_{II}$ 에서 아래 조건을 만족하는 세 쌍만 선택해 $K_{III}$에 저장한다.

$K_I \sim K_{III}$의 과정을 살펴보면 모델과 센싱 클라우드 포인트 데이터에서 feature 계산하고 두 군집 속에서 특징이 가장 비슷한 같은 포인트 쌍 세 개를 keypoint로 사용하겠다는 것이다.