DP! 🟥🟧🟨🟩🟦🟪🟫⬜⬛🫢🔔😎😊🤔😭⭐
DP
토끼 쌍의 수 구하기
n번째 달의 토끼 쌍의 수는?
첫날에는 한쌍
두달 이상이 된 토끼는 번식 가능
가능한 한쌍은 매달 새끼 한 쌍을 낳는다
토끼는 죽지 않는다
1 1 2 3 5 8 13 21 ...
피보나치 수열
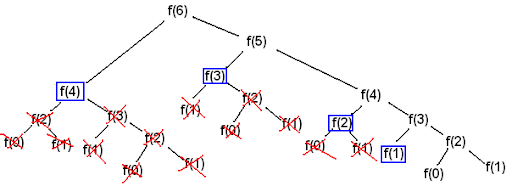
상태공간트리를 그려보자!
중복 호출이 너무 많다..
메모이제이션
컴퓨터 프로그램을 실행할 때 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적인 실행속도를 빠르게 하는 기술
중복 부분문제 구조
DP는 큰 문제를 이루는 작은 문제들을 먼저 해결하고 작은 문제들의 최적 해(Optimal Solution)를 이용하여 순환적으로 큰 문제를 해결한다.
DP는 문제의 순환적인 성질 때문에 이전에 계산되어졌던 작은 문제의 해가 다른 어딘가에서 필요하게 되는데 이를 위해 DP에서는 이미 해결된 작은 문제들의 해들을 어떤 저장 공간(table)에 저장하게 된다.
그리고 이렇게 저장된 해들이 다시 필요할 때 마다 해를 얻기 위해 다시 문제를 재계산하지 않고 table의 참조를 통해서 중복된 계산을 피하게 된다.
최적 부분문제 구조
동적 계획법이 최적화에 대한 어느 문제에나 적용될 수 있는 것은 아니다. 주어진 문제가 최적화의 원칙(Principle of Optimality)을 만족해야만 동적 계획법을 효율적으로 적용할 수 있다.
최적화의 원칙이란 어떤 문제에 대한 해가 최적일 때 그 해를 구성하는 작은 문제들의 해 역시 최적이어야 한다는 것이다. 동적 계획법의 방법 자체가 큰 문제의 최적해를 작은 문제의 최적해들을 이용하여 구하기 때문에 만약 큰 문제의 최적해가 작은 문제들의 최적 해들로 구성되지 않는다면 이 문제는 동적 계획법을 적용할 수 없다.
분할정복 vs DP
분할정복은 단순히 문제를 부분으로 나누어 해결한다!
부분문제들이 서로 연관이 없음!
vs
DP는 부분문제들의 해를 이용하여 최적해를 구해낸다!
부분문제들이 같은 경향을 가지고 있음
DP 적용 접근 방법
-
최적해 구조의 특성을 파악하라
-
최적해의 값을 재귀적으로 정의하라
-
상향식 방법으로 최적해의 값을 계산하라
백준 12865번
정답코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int n,k;
static int[] w,v;
static int[][] dp;
static int res;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
w = new int[n+1];
v = new int[n+1];
dp = new int[n+1][k+1];
res = Integer.MIN_VALUE;
for(int i=1;i<=n;i++) {
st = new StringTokenizer(br.readLine());
w[i] = Integer.parseInt(st.nextToken());
v[i] = Integer.parseInt(st.nextToken());
}
for(int i=1;i<=n;i++) {
for(int j=1;j<=k;j++) {
int max = 0;
// 담기
if(j-w[i] >= 0) {
if(dp[i-1][j-w[i]] + v[i] > max) {
max = dp[i-1][j-w[i]] + v[i];
}
}
// 안담기
if(dp[i-1][j] > max) {
max = dp[i-1][j];
}
dp[i][j] = max;
}
}
System.out.println(dp[n][k]);
}
}