04.07 학습&숙제

Knapsack! 🟥🟧🟨🟩🟦🟪🟫⬜⬛🫢🔔😎😊🤔😭⭐

배낭 채우기

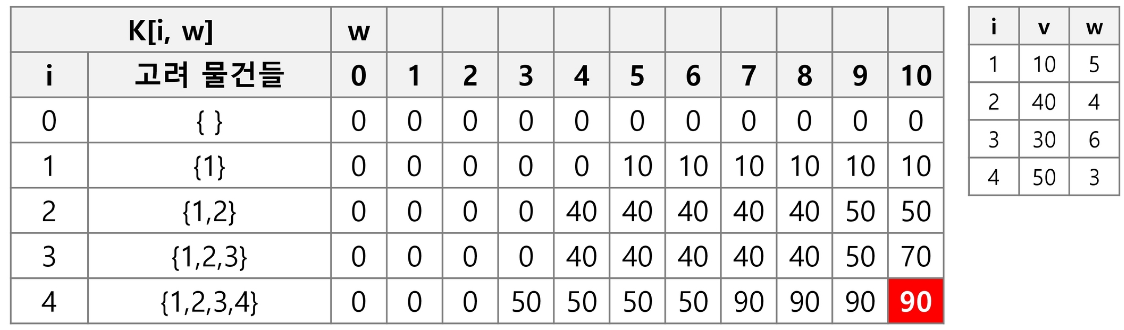
배낭 문제는 n개의 물건과 각 물건 i의 무게 w와 가치 v가 주어지고, 배낭의 용량은 W일 때, 배낭에 담을 수 있는 물건의 최대 가치를 찾는 문제이다. 단, 배낭에 담은 물건의 무게의 합이 W를 초과하지 말아야 한다.

완전 탐색

물건들의 집합 S에 대한 모든 부분 집합 중에 최적의 부분집합을 찾는다 -> 2^n

그리디

모든 상황에 반례가 존재 (Fractional Knapsack은 가능)

DP

문제를 1~n개의 물건을 순서대로 담는 것과, 0~W 부터 최적해를 만들어서 접근

0/1 Knapsack

추가 고민

🤔 공간 복잡도 개선이 가능한가?

DP 테이블을 채우는 과정에서 필요한 것은 바로 윗 줄만 필요하다
-> 두 줄로 가능

뒤에서 채우면 한 줄로도 가능하다🫢

🤔 물건을 여러 개 담는 것이 가능하다면?

앞에서부터 계속 담는다!

백준 13708번: 물벼룩의 생존확률

정답코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
	static int n,k;
	static long[][] dp;
	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		
		st = new StringTokenizer(br.readLine());
		k = Integer.parseInt(st.nextToken());
		n = Integer.parseInt(st.nextToken());
		
		dp = new long[200][130];
		
		long cnt = go(k+64,n);
		
		System.out.println(cnt);
		
	}
	private static long go(int k, int n) {
		if(k <= 64) return 0;
		if(n == 0) {
			if(k > 64) return 1;
			if(k <= 64) return 0;
		}
		if(dp[k][n] != 0) {
			return dp[k][n];
		}
		
		long sum = 0;
		sum += go(k+1,n-1);
		sum += go(k-1,n-1);
		
		dp[k][n] = sum;
		
		return sum;
	}
}

풀이

냅색 문제는 아니지만 풀어본 dp 문제 음수 인덱스를 대비해서 63번 점프를 하니깐 64부터 체크한다
탑다운 방식으로 메모이제이션을 통해 푼 문제

숙제

정처기 실기 1장 마무리 하기