마르코프 프로세스 (Markov Process)

아이가 잠이 드는 마르코프 프로세스

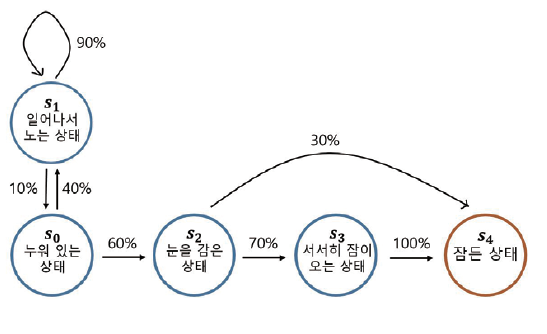
• 아이가 취할 수 있는 상태 의 종류는 총 5가지입니다.

  • 누워있는 상태 s0
  • 일어나서 노는 상태 s1
  • 눈을 감고 있는 상태 s2
  • 서서히 잠이 오는 상태 s3
  • 마침내 잠이 든 상태 s4

• 아이는 상태 s0 에서 시작하여 미리 정해진 확률에 따라 상태 전이 를 합니다.

  • 상태 전이는 현재 상태에서 다음 상태로 넘어간다는 것의 다른 말입니다.

• s4 는 종료 상태이고, 여기에 도달하는 순간 마르코프 프로세스는 끝이 납니다.

다시, 마르코프 프로세스

• 앞서 보았던 것처럼 마르코프 프로세스는 미리 정의된 어떤 확률 분포를 따라서 상태와 상태 사이를 이동해 다니는 여정입니다.

• 어떤 상태에 도착하게 되면 그 상태에서 다음 상태가 어디가 될지 각각에 해당하는 확률이 있고, 그 확률에 따라 다음 상태가 정해집니다.

• 마르코프 프로세스를 엄밀하게 정의하기 위해서는 2가지 요소가 필요합니다.

• 상태의 집합 S

  • 가능한 상태들을 모두 모아놓은 집합입니다. 아이가 잠드는 마르코프 프로세스의 경우에는 이 집합의 원소가 5개로, S = {s0, s1, s2, s3, s4} 였습니다.

• 전이 확률 행렬 P

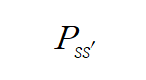
• 전이 확률 Pss' 는 상태 s 에서 다음 상태 s' 에 도착할 확률을 가리킵니다.

• Pss' 을 조건부 확률을 이용해서 조금 다른 방식으로 표현해 볼 수 있습니다.

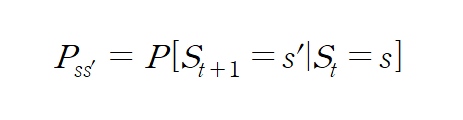
• 시점 t 에서의 상태가 s 였다면 t+1 에서의 상태가 s' 이 될 확률이라는 뜻입니다.

마르코프 성질

• "미래는 오로지 현재에 의해 결정된다"

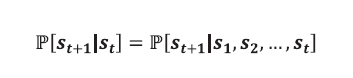
• 마르코프 프로세스에서 다음 상태가 s(t+1) 이 될 확률을 계산하려면 현재의 상태 st 가 무엇인지만 주어지면 충분하다는 뜻입니다.

  • 다시 말해, 미래는 오로지 현재에 의해 결정되는 것입니다.

마르코프한 상태 - 체스 게임

• 체스 게임에서는 현재 상황에서 해야 하는 일과 과거 경기 양상이 어떠했는지 여부는 아무런 관련이 없습니다.

  • 당장 맞닥뜨린 상황을 잘 읽고 미래를 내다보며 최선의 수를 둬야 하는 것입니다.

마르코프 하지 않은 상태 - 운전

• 운전하고 있는 운전자의 상태를 생각해 봅시다.

• 운전을 하고 있는 상태의 특정 시점에 사진을 찍어서 해당 사진으로만 운전을 지속해야 한다고 가정해봅시다.

• 이 사진만 가지고 브레이크를 밟아야 할지, 엑셀을 밟아야 할 지 알 수 없습니다.

  • 따라서 사진만 가지고 구성한 운전자의 상태는 마르코프한 상태가 아닙니다.

• 하지만 "최근 10초 동안의 사진 10장을 묶어서" 상태로 제공한다면, 이 상태는 마르코프 상태라고 볼 수 있습니다.

  • 완전히 마르코프한지는 모르겠지만, 적어도 마르코프한 상태에 더 가까워졌다는 것은 의심의 여지가 없을 것입니다.

• 또한, 굳이 사진을 묶지 않더라도 특정 시점에 사진과 더불어 속도 벡터, 가속도 벡터 등을 함께 제공한다면 이 또한 마르코프 성질을 더 잘 만족시킬 수 있습니다.

마르코프 리워드 프로세스 (Markov Reword Process)

• 마르코프 프로세스에 보상의 개념이 추가되면 마르코프 리워드 프로세스 가 됩니다.

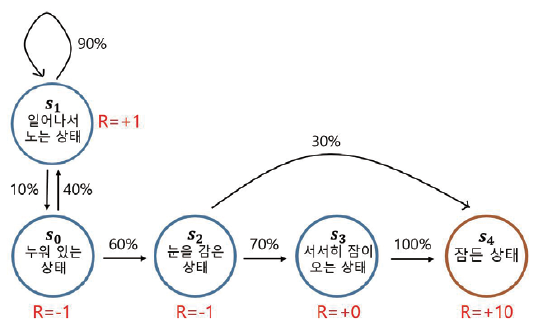
아이가 잠이 드는 MRP

• 아까 보았던 아이가 잠이 드는 MP 에 빨간 색으로 보상 값이 추가된 것을 확인할 수 있습니다.

  • 이제는 어떤 상태에 도착하게 되면 그에 따르는 보상을 받게 되는 것이죠.

• 마르코프 프로세스는 상태의 집합 S 와 전이 확률 행렬 P 로 정의 되었는데, MRP 를 정의하기 위해서는 R 과 γ 라는 2가지 요소가 추가로 필요합니다.

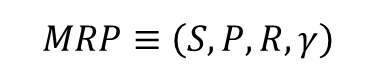
• 상태의 집합 S

  • 마르코프 프로세스의 S 와 같고, 상태의 집합입니다.

• 전이 확률 행렬 P

  • 마르코프 프로세스의 P 와 같고, 상태 s 에서 상태 s' 으로 갈 확률을 행렬의 형태로 표현한 것입니다.

• 보상 함수 R

  • R 은 어떤 상태 s 에 도착했을 때 받게 되는 보상을 의미합니다.

• 기댓값이 등장하는 이유는 특정 상태에 도달했을 때 받는 보상이 매번 조금씩 다를 수도 있기 때문입니다.

  • 예컨데 어떤 상태에 도달하면 500원짜리 동전을 던져서 앞면이 나오면 500원을 갖고 뒷면이 나오면 갖지 못한다고 할 때, 보상의 값이 매번 바뀌지만 그 기댓값은 250원으로 정해지게 됩니다.

• 감쇠 인자 γ

  • γ 은 0에서 1사이의 숫자입니다.
  • 이는 강화 학습에서 미래 얻을 보상에 비해 당장 얻는 보상을 얼마나 더 중요하게 여길 것인지를 나타내는 파라미터입니다.
  • 구체적으로는 미래에 얻을 보상의 값에 γ 가 여러 번 곱해지며 그 값을 작게 만드는 역할을 합니다.

• 감쇠 인자 γ 을 자세하게 설명하기 전에, 현재부터 미래에 얻게 될 보상의 합을 가리키는 리턴 이라는 개념을 먼저 설명하겠습니다.

감쇠된 보상의 합, 리턴

• MRP 에서는 MP 와 다르게 상태가 바뀔 때마다 해당하는 보상을 얻습니다.

  • 상태 s0 에서 보상 R0 을 받고 시작하여 종료 상태인 sT에 도착할 때 보상 RT 를 받으며 끝이 납니다.

• 그러면 s0 에서 시작하여 sT 까지 가는 여정을 다음과 같이 표현할 수 있습니다.

  

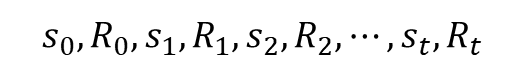
• 이와 같은 하나의 여정을 강화 학습에서는 에피소드 라고 합니다.

• 이런 표기법을 이용하여 바로 리턴 Gt 를 정의할 수 있습니다.

  • 리턴이란 t 시점부터 미래에 받을 감쇠된 보상의 합을 말합니다.

  

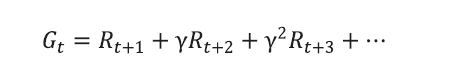
• 현재 타임 스텝이 t 라면 그 이후에 발생하는 모든 보상의 값을 더해줍니다.

• 또 현재에서 멀어질수록, 즉 더 미래에 발생할 보상일수록 γ 가 여러 번 곱해집니다.

  • γ는 0에서 1 사이의 실수이기 때문에 여러 번 곱해질수록 그 값은 점점 0에 가까워집니다.

• 따라서 γ 의 크기를 통해 미래에 얻게 될 보상에 비해 현재 얻는 보상에 가중치를 줄 수 있습니다.

• "강화 학습은 보상을 최대화 하도록 학습하는 것이 목적이다"라는 말은 엄밀하게 이야기하면 틀린 말입니다.

  • 강화 학습은 보상이 아니라 리턴을 최대화 하도록 학습하는 것입니다.
  • 다시말해, 보상의 합인 리턴이 바로 우리가 최대화하고 싶은 궁극의 목표입니다.

γ는 왜 필요할까?

• 앞서 말했듯, 감마는 미래를 평가 절하해주는 항입니다.

• 이런 γ가 꼭 필요한 이유에 대해 3가지 관점에서 이야기해 보겠습니다.

수학적 편리성

• γ 를 1보다 작게 해줌으로써 리던 Gt 가 무한의 값을 가지는 것을 방지할 수 있습니다.

  • 리턴이 무한한 값을 가질 수 없게 된 덕분에 이와 관련된 여러 이론들을 수학적으로 증명하기가 한결 수월해집니다.

• 좀 더 쉽게 이야기하면, 에피소드에서 얻는 각각의 보상의 최댓값이 정해져 있다면, Gt 는 유한하다는 것입니다.

  • γ 덕분에 MRP 를 무한한 스텝동안 진행하더라도 리턴 Gt 는 절대 무한한 값이 될 수 없습니다.

• 리턴이 무한이라면 어느 쪽이 더 좋을지 비교하기도 어렵고, 그 값을 정확하게 예측하기도 어려워집니다.

  • 감마가 1보다 작은 덕분에 이 모든 것이 가능해집니다.

사람의 선호 반영

• 사람은 기본적으로 눈앞의 보상을 더 선호합니다.

• 예를 들어, 사람은 당장 100만원을 받는 것을 5년 후에 100만원을 받는 것보다 선호합니다.

• 이런 이유에서 에이전트를 학습하는데 있어서 감마의 개념을 도입합니다.

미래에 대한 불확실성 반영

• 현재와 미래 사이에는 다양한 확률적 요소들이 있고 이로 인해 당장 느끼는 가치에 비해 미래에 느끼는 가치가 달라질 수 있습니다.

  • 그렇기 때문에 미래의 가치에는 불확실성을 반영하고자 감쇠를 해줍니다.

MRP 에서 각 상태의 밸류 평가하기

• 아이가 잠드는 MRP 에서 눈을 감고 있는 상태 s2의 밸류 혹은 가치를 숫자 하나로 평가한다고 해봅시다.

• 어떤 상태를 평가할 때에는 그 시점으로부터 미래에 일어날 보상을 기준으로 평가해야 합니다.

  • 그러니 아이가 잠드는 MRP 에서 아이가 눈을 감고 있는 상태를 평가하고자 한다면 마찬가지로 해당 상태를 지나 미래에 받을 보상들을 더해야 합니다.
    -> 이것이 바로 리턴입니다.

• 하지만 리턴이라는 값은 매번 바뀐다는 문제가 있습니다.

  • 왜냐하면 MRP 자체가 확률적인 요소에 의해 다음 상태가 정해지기 때문에 같은 s2 에서 출발해도 아이가 잠들 때까지 각기 다른 상태를 방문하며 그때마다 얻는 리턴의 값은 달라지기 때문입니다.

• 이러한 이유 때문에 리턴의 기댓값 을 사용하는 것입니다.

• 하지만 논의를 이어가기 전에 "에피소드를 샘플링한다"라는 개념을 설명하고, 그에 따라 정말 매번 다른 리턴 값을 얻게 되는지를 확인하고 넘어가겠습니다.

에피소드의 샘플링

• 하나의 에피소드 안에서 방문하는 상태들은 매번 다릅니다. 그리고 그에 따라 리턴도 달라집니다.

  • 즉, 매번 에피소드가 어떻게 샘플링 되느냐에 따라 리턴이 달라집니다.

• 샘플링이란, 말그대로 샘플을 뽑아본다는 뜻을 가집니다.

  • 어떤 확률 분포가 있을 때 해당 분포에서 샘플을 뽑아보는 것이 샘플링입니다.

• 예를 들어 앞뒷면의 확률이 반반인 동전 X의 확률 분포는 다음과 같습니다.

  • P(X = 앞면) = 0.5
  • P(X = 뒷면) = 0.5

• 이를 샘플링 해보면, 즉 동전을 던져보면, 앞면 또는 뒷면이 나옵니다.

  • 이 때 나온 하나의 면을 샘플이라고 합니다.

• 우리는 주어진 확률 분포에서 샘플링을 계속해서 할 수 있습니다.

• 정리하면 위와 같은 샘플링 기법을 통해 주어진 MRP 에서 여러 에피소드를 샘플링해 볼 수 있습니다.

  • 각 상태에서 마치 동전 던지기와 같은 과정을 거쳐서 다음 상태가 정해집니다.
  • 각 상태마다 다음 상태를 샘플링하며 진행하면 언젠가 종료 상태에 도달할 것이고 하나의 에피소드가 끝이 납니다.

• 중요한 것은, 우리에게 전이 확률 행렬 P 가 주어져 있기 때문에 이런 샘플들을 원한다면 무한히 뽑아낼 수 있다는 점입니다.

상태 가치 함수 (State Value Function)

• 상태를 인풋으로 넣으면 그 상태의 밸류를 아웃풋으로 출력하는 함수

• 앞서 살펴본 것처럼 에피소드마다 리턴이 다르기 때문에 어떤 상태 s의 밸류 v(s)는 기댓값을 이용하여 정의합니다.

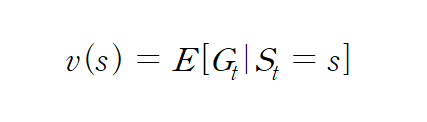
• 조건부로 붙는 St = s 의 의미는 시점 t 에서 상태 s 부터 시작하여 에피소드가 끝날 때까지의 리턴을 계산하라는 뜻이 됩니다.

• 아이가 잠드는 MRP 에서 상태 s0 에서 출발하여 발생할 수 있는 에피소드는 무한히 많고, 그때마다 리턴도 항상 다릅니다.

• 기댓값을 구하려면 에피소드별로 해당 에피소드가 발생할 확률과 그때의 리턴 값을 곱해서 더해주어야 합니다.

  • 가능한 에피소드가 무한히 많기 때문에 이런 접근법은 현실적으로 불가능합니다.

• 그래서 간단한 방법은 샘플로 얻은 리턴의 평균을 통해 밸류를 근사하게나마 계산해볼 수 있습니다.

  • 더 정확한 방법은 추후에 다루도록 하겠습니다.

마르코프 결정 프로세스 (Markov Decision Process)

• 앞서 소개했던 MP 와 MRP 에서는 상태 변화가 자동으로 이루어졌습니다.

  • 따라서 MP 나 MRP 만 가지고는 순차적 의사결정 문제를 모델링 할 수 없습니다.
  • 순차적 의사결정에서는 의사결정 이 핵심이기 때문입니다.

• 이러한 이유로 마르코프 결정 프로세스(Markov Decision Process) 가 등장합니다.

MDP 의 정의

• MDP 는 MRP 에 에이전트가 더해진 것입니다.

  • 에이전트는 각 상황마다 액션(행동)을 취합니다.
  • 해당 액션에 의해 상태가 변하고 그에 따른 보상을 받습니다.

• 이 때문에 MDP 를 정의하기 위해서는 액션의 집합 A 라는 요소가 추가됩니다.

  • A 가 추가되면서 기존의 전이 확률 행렬 P 나 보상 함수 R 의 정의도 MRP 에서의 정의와 약간씩 달라지게 됩니다.

• 정리하면 MDP 의 구성요소는 (S, A, P, R, γ) 입니다.

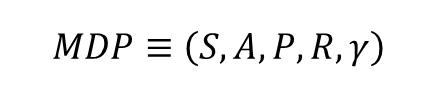
• 상태의 집합 S

  • MP 와 MRP 에서의 S 와 같습니다. 가능한 상태의 집합입니다.

• 액션의 집합 A

  • 에이전트가 취할 수 있는 액션들을 모아놓은 것입니다.
  • 에이전트는 스텝마다 액션의 집합 중에서 하나를 선택하여 액션을 취하며, 그에 따라 다음에 도착하게 될 상태가 달라집니다.

• 전이 확률 행렬 P
  

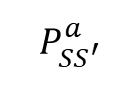
  • MDP 에서는 에이전트가 선택한 액션에 따라서 다음 상태가 달라집니다.
  • 따라서 "현재 상태가 s 이며 에이전트가 액션 a 를 선택했을 때 다음 상태가 s' 이 될 확률" 을 정의해야 합니다.

    • 여기서 주의해야 할 부분은 상태 s 에서 액션 a 를 선택했을 때 도달하게 되는 상태가 결정론적이 아니라는 점입니다.
    • 같은 상태 s 에서 같은 액션 a 를 선택해도 매번 다른 상태에 도착할 수 있습니다.
    • 말하자면 액션 실행 후 도달하는 상태 s' 에 대한 확률 분포가 있고 그게 바로 전이 확률 행렬 P 입니다.

• 조건부 확률의 개념을 이용한 전이 확률 행렬 P 의 엄밀한 정의는 다음과 같습니다.

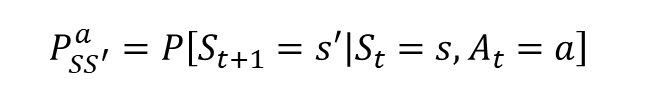
• 보상 함수 R

  • MDP 에서는 액션이 추가 되었기 때문에 현재 상태 s 에서 어떤 액션을 선택하느냐에 따라 받는 보상이 달라집니다.
  • 이를 반영하기 위해 R 에도 액션을 가리키는 a 의 첨자가 하나 붙게 됩니다.

• 상태 s 에서 액션 a 를 선택하면 받는 보상을 가리키며, 이는 확률적으로 매번 바뀔 수 있기 때문에 마찬가지로 기댓값을 이용하여 표기합니다.

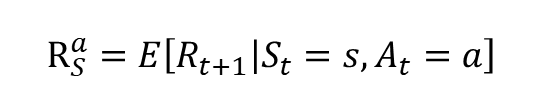
• 감쇠 인자 γ

  • MRP 에서의 γ 와 정확히 같습니다.

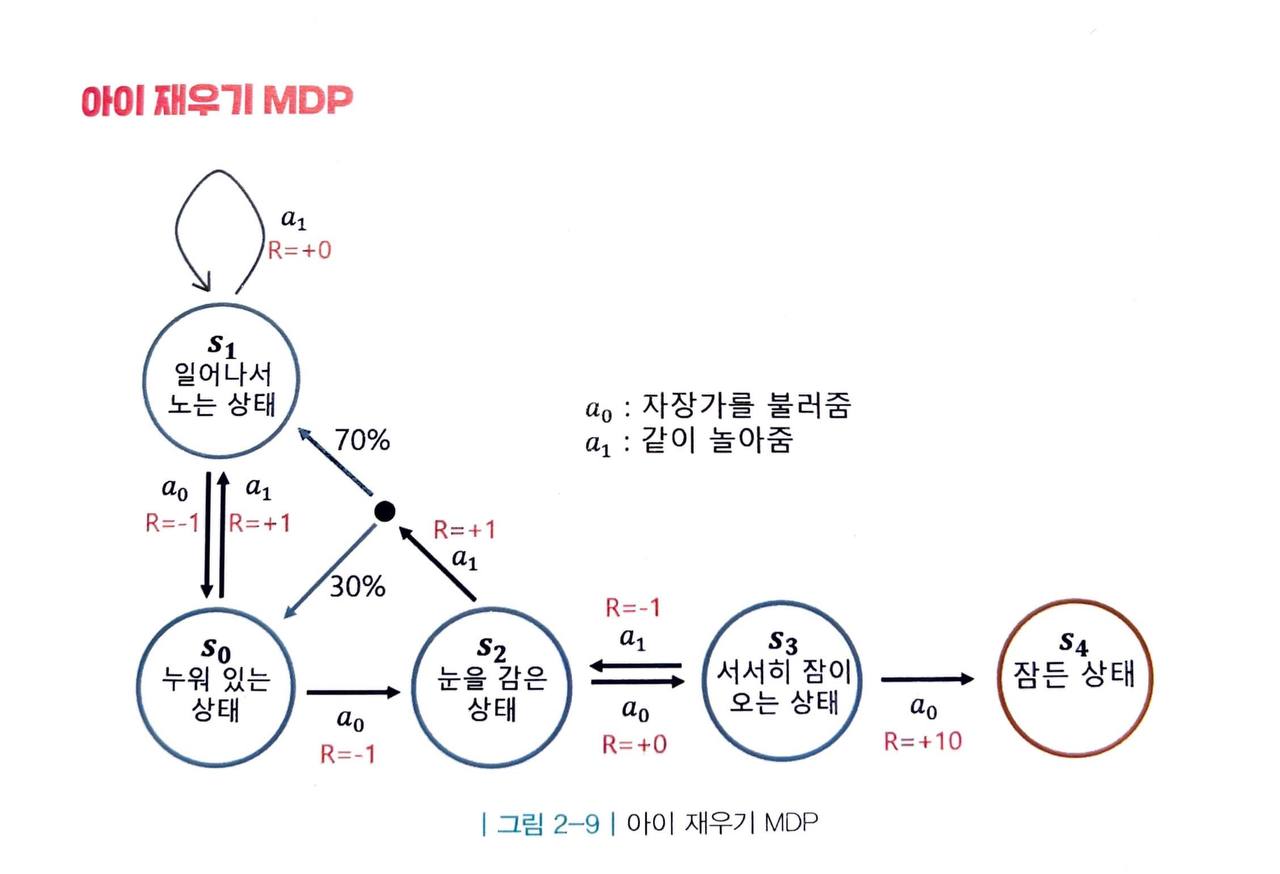
아이 재우기 MDP

• 아이가 잠드는 상황에서 어머니라는 에이전트가 개입되기 시작하였습니다.

  • 어머니가 선택할 수 있는 액션은 자장가를 불러주는 액션 a0 와 함께 놀아주는 액션 a1 2가지가 있습니다.

• 눈여겨 볼 부분은 아이가 눈을 감은 상태인 s2 에서 아이를 놀아주는 액션을 선택하면 아이의 다음 상태는 그날 아이의 상태에 따라 s0 가 될 수도 있고, s1 이 될 수도 있습니다. 이때의 전이 확률을 수식으로 표현하면 다음과 같습니다.

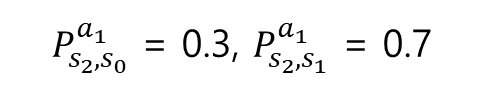
• 그렇다면 아이 재우기 MDP 에서 보상의 합을 최대화하기 위해서 어머니는 어떤 행동을 선택해야 할까요?

  • 자세히 관찰하면 계속해서 a0 만을 선택하면 최적이라는 것을 어렵지 않게 알 수 있습니다.

• 이처럼 MDP 가 간단한 경우는 최적의 전략을 찾기 쉬웠습니다.

  • 반면 실제 세계에서 마주하는 MDP 는 상태의 개수 및 액션의 개수가 훨씬 많기 때문에 최적 행동을 찾는 것이 그렇게 쉽지만은 않습니다.

• 따라서 이러한 상황에서도 좋은 전략(=정책)을 찾는 것이 우리의 목적입니다.

정책 함수와 2가지 가치 함수

정책 함수

• 각 상태에서 어떤 액션을 선택할지 정해주는 함수

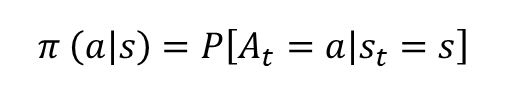
• 확률을 이용한 정의는, 상태 s 에서 액션 a 를 선택할 확률로 해석할 수 있습니다.

상태 가치 함수

• MDP 에서는 에이전트의 정책 함수에 따라서 얻는 리턴이 달라집니다.

  • 따라서 가치 함수는 정책 함수에 의존적입니다.

• π 가 주어졌다고 가정했을 때 가치 함수의 정의는 다음과 같습니다.

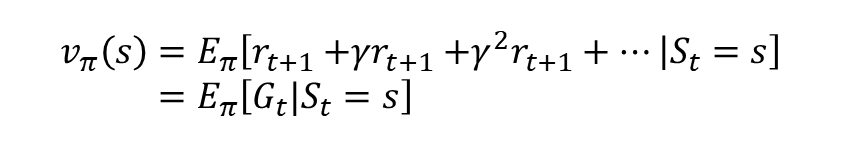
• 이는 s 부터 끝까지 π 를 따라서 움직일 때 얻는 리턴의 기댓값입니다.

  • 이 식은 정책 함수를 π 로 고정해놓고 생각한 것입니다.

액션 가치 함수

• 액션 가치 함수는 q(s, a)로 표현합니다.

  • 상태에 따라 액션의 결과가 달라지기 때문에 상태와 액션이 동시에 인풋으로 들어가야 합니다.

• 마찬가지로 π 를 고정시켜 놓고 평가합니다.

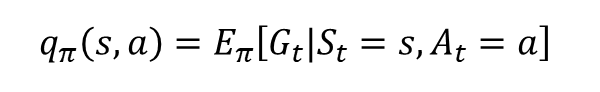
• 이는 s 에서 a 를 선택하고, 그 이후에는 π 를 따라서 움직일 때 얻는 리턴의 기댓값입니다.

• 일단 s 에서 a 를 선택하고 나면 이후의 상태를 진행하기 위해 계속해서 누군가가 액션을 선택해야 하는데, 그 역할은 정책 함수 π 에게 맡기는 것입니다.

• 따라서 v(s) 와 q(s, a) 는 "s 에서 어떤 액션을 선택하는가" 하는 부분에만 차이가 있습니다.

  • v(s) 를 계산할 때는 s 에서 π 가 액션을 선택하는 반면, q(s, a) 를 계산할 때는 s 에서 강제로 a 를 선택합니다.
  • 일단 액션을 선택한 이후에는 2가지 가치 함수 모두 정책 함수 π 를 따라서 에피소드가 끝날 때까지 진행합니다.

Prediction 과 Control

Prediction

• π 가 주어졌을 때 각 상태의 밸류를 평가하는 문제

  • 즉, 임의의 정책 π 에 대해 각 상태의 밸류 v(s) 를 구하고자 하는 것

Control

• 최적 정책 π* 를 찾는 문제

  • 최적의 정책이란 이 세상에 존재하는 모든 π 중에 가장 기대 리턴이 큰 π 를 뜻합니다.

• 최적 정책 π 를 따를 때의 가치 함수를 최적 가치 함수 라고 하며 v 라고 표기합니다.

  • π 와 v 를 찾았다면 "이 MDP 는 풀렸다" 고 말할 수 있습니다.

Reference

• 노승은(2020), 바닥부터 배우는 강화 학습