[CV] How to find the weights?

hmin·2024년 4월 5일

Computer Vision

목록 보기

2/8

이준석 교수님의 유튜브 강의 Lec3 Loss functions & Optimization 영상을 참고해서 정리한 내용입니다. 다른 출처표기가 없는 이미지는 유튜브 영상에서 가져온 것임을 밝힙니다.
https://www.youtube.com/watch?v=FHRkxoF9nl0

이전 포스팅 에서 가장 기본적인 두 image classification 방식들에 대해 다루었다. 그 중 두 번째로 다루었던 Linear Classification 을 이용해서 가중치를 어떻게 업데이트 시키고, 모델을 학습하는 방식에 대해 다뤄볼 예정이다.

How to find the Weights

가장 간단한 구조인 linear classifier에도 Weight matrix부터 bias 등 상당히 많은 파라미터가 있었다. 그럼 linear classification에서 가장 중요한 가중치 혹은 파라미터 는 어떻게 학습시키는 것인가?

머신러닝은 결국 Data-driven 접근 방식이기 때문에 당연히 가중치도 데이터들로 부터 학습해야 한다. 이미지가 들어왔을 때 나의 예측과 실제 정답이 얼마나 다른지(Loss function) 측정한 후에 이를 기반으로 가중치를 업데이트(Optimization) 시켜야 한다. 다음에 나올 예시들을 통해 감을 잡아보자.

1) Discriminative Setting

binary classification에서 클래스가 y = {+1, -1}이라고 하자. 즉 한 클래스는 양수, 다른 클래스는 음수인 두 클래스를 분류하는 문제이다.

이때 Loss는 $y\hat{y}$ 으로 결정될 수 있다. 옳게 예측한 경우에 양수 클래스든 음수 클래스든 $y\hat{y} >0$ 이 된다. 하지만 틀리게 예측한 경우에는 $y \hat{y} <0$ 이 된다.

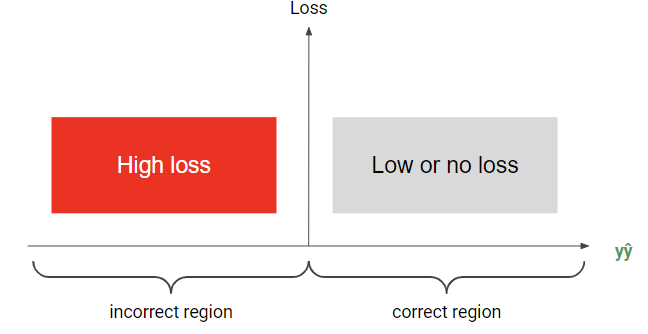
이를 좌표평면으로 표현해보면 위와 같다. $y\hat{y}$ 값이 더 커질수록 강한 confidence로 맞췄다는 의미가 되며, 더 작아진다면 강한 confidence를 가졌지만 틀렸다는 의미가 된다(자신있게 틀림..😂) . 그럼 이에 맞는 패널티를 줄 수 있게끔 Loss function을 만들어보자.

loss function은 정말 다양하게 만들 수 있지만, 우선 잘 알려진 함수 네 가지를 살펴보자.

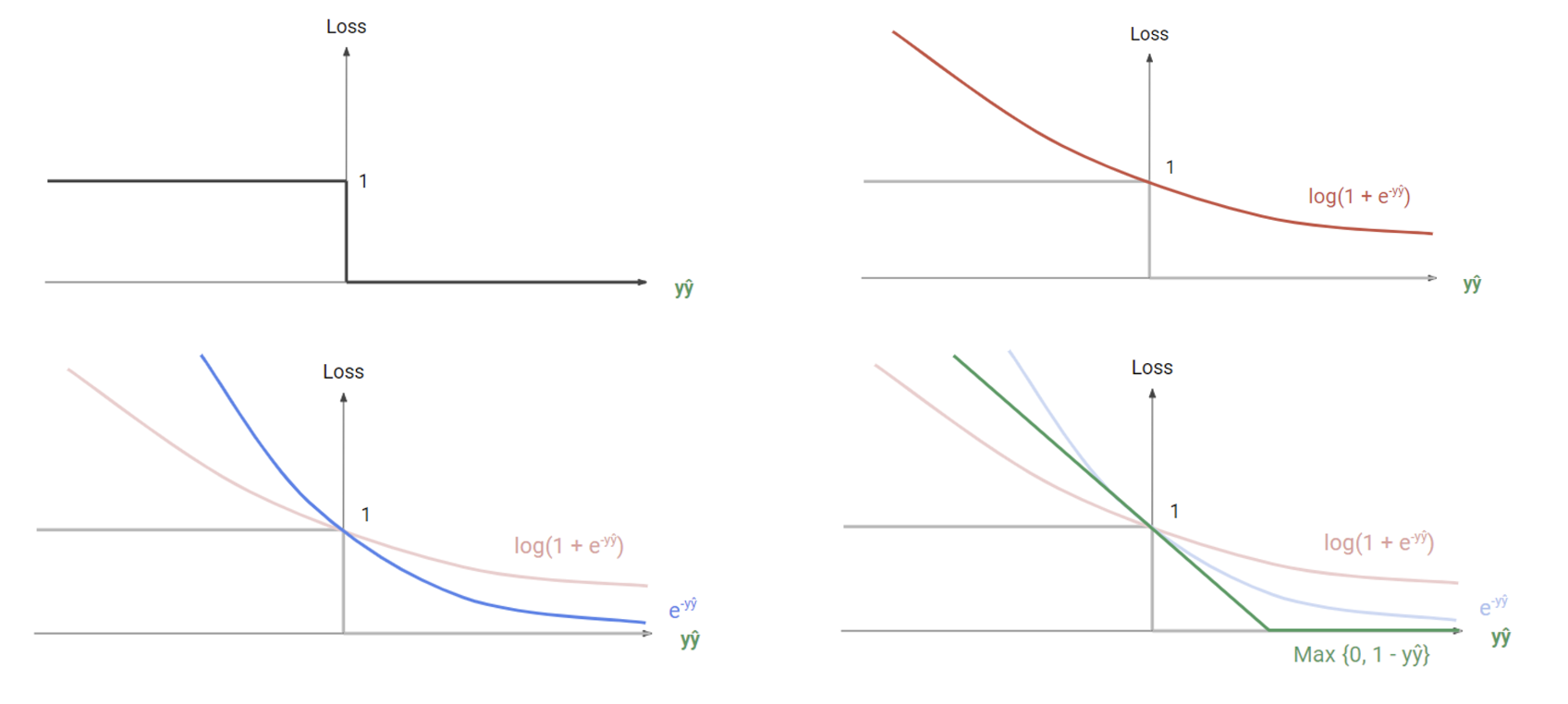
위에 부터 0/1 loss, Log loss, 아래에 Exponential loss, Hinge loss 함수이다. 하나씩 어떤 성질을 가지고 있는지 알아보자.

0/1 Loss

가장 간단하면서도 직관적으로 그릴 수 있는 로스 함수. $y \hat{y}>0$ 일 땐 패널티가 0이고 <0일 땐 패널티가 1인 step function이다. 하지만 가장 큰 문제점은 $y \hat{y}=0$ 에서 미분이 불가능하다는 점.

Loss함수를 이야기 할 때 미분 가능 여부가 왜 중요할까?

뒤에서 더 자세한 설명이 나오겠지만 직관적으로 먼저 생각해보자. $y \hat{y}=0$ 인 지점은 매우 중요한 기준점이다. 기준점에서 부터 조금만 플러스면 바로 패널티가 없어지고, 조금만 마이너스면 바로 패널티가 강하게 들어온다. 즉, 패널티 여부를 결정짓는 가장 중요한 경계값에서 미분이 불가능하다면 모델에게 정확한 학습 방향을 가리키는게 사실상 어렵기도 하고 애매모호 해진다. 따라서 로스 함수에서는, 특히 중요한 결정을 하는 기준점에서는 미분 가능성이 매우 중요하게 작동한다.

Log Loss

그럼 실수 전체에 대해 미분 가능하게 만들면 되는거 아닌가? 하는 아이디어에서 도입된 로그 로스 함수. 정답을 맞았더라도 확신이 덜 하다면 패널티를 줘서 더욱 확신있게 맞추도록 한다.

Exponential Loss

로그 로스와 비슷하지만 로그 함수는 기울기에 큰 차이가 없기 때문에 문제를 틀렸을 때에 더 큰 기울기를 줘서 변화가 크게끔 만든 함수.

Hinge Loss

일차 함수와 결합하면서 margin을 둠으로써 확신 없이 맞춘 경우에도 패널티를 주어 모델이 더 확신있게 정답을 맞추도록 만든다. 하지만 여기서도 미분 불가능 점이 있지만 여기서는 0/1 Loss와는 다르게 상대적으로 중요하지 않은 점에 대해서 불가능하므로 큰 문제가 없다.

➕ 계산이 매우 간단한 장점이 있다. (미분값이 0 또는 상수값)

2) Probabilistic Setting

사실 이전에 봤던 deterministic한 환경보다 훨씬 많이 쓰이는 방법이 바로 확률 세팅이다. 여기선 Binary classification에 대해 ground truth가 y={0, 1}이 된다. 하나의 클래스에 대한 예측 확률을 $\hat{y}$ 이라 하면 다른 클래스에 대한 확률은 $1-\hat{y}$ 이 된다. 여기서 sigmoid 를 이용해 라벨을 예측할 수 있다.

확률 세팅으로는 multi class로 확장이 용이하다. y를 one-hot vector로 주고 softmax 를 이용해 라벨을 예측할 수 있다.

Cross Entropy Loss

probabilistic setting에서 가장 많이 쓰이는 로스 함수. 우선 cross entropy 함수가 어떻게 생겼는지 보자.

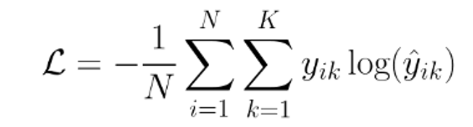
i번째 샘플에 대해서 클래스 k를 예측하는 것이다. Notation을 정리해 보자면,

$y_{ik}$ = i번째 샘플이 k 클래스에 속하면 1, 속하지 않으면 0인 ground truth

$\log (\hat{y}_{ik})$ = i번째 샘플이 k 클래스에 속할 예측값(확률)

📌 근데 여기서 -1/N이 앞에 곱해지는 이유는 뭘까?

생각해보면 y는 one-hot vector이기 때문에 정답인 클래스에 대해서만 1이고 나머지는 0이다. 즉 위의 시그마를 풀어보면 결국 정답이 아닌 클래스에 대해서는 0으로 없어지고, 정답인 클래스에 대해서만 아래와 같이 정리된다.

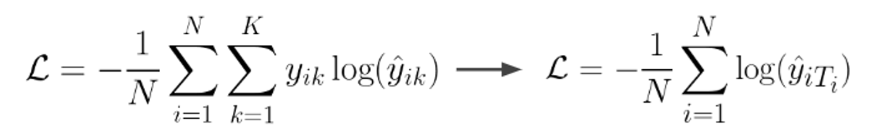
이때 $T_i$ 를 i번째 샘플의 ground truth 인덱스라고 하면 결국 오른쪽 식처럼 정답인 클래스에 대해서만 예측값이 남는다. 따라서 N개의 샘플에서 클래스 T에 속할 로그 확률을 평균 내는 것과 동일하다.

그럼 앞에 -가 붙은 이유는 뭘까?

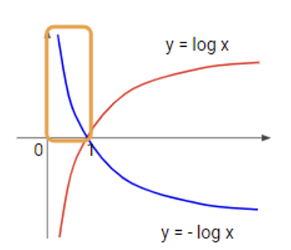
결국 $\hat {y}_{iT_i}$ 도 확률값으로 0과 1사이의 값을 가지며, $y = -\log x$ 함수에서 보면 노란색 박스 부분이 된다. 1에 가까워 질수록 로스 값(패널티)이 0에 수렴하고, 0에 가까워 질수록 로스 값이 무한대로 증가하는 부분만 떼서 로스 함수로 쓰는 것이다.

즉 cross entropy를 쓰면 정답인 클래스에 대한 -log 값의 평균을 로스로 사용할 수 있다는 점!

KL Divergence

두 분포의 차이를 나타내는 함수. Distance처럼 쓰이지만 사실상 완전히 Distance라 정의할 수는 없다.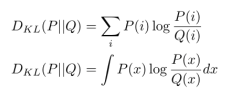

이유는 P와 Q의 순서가 다르면 값도 달라지기 때문에. 하지만 그럼에도 자주 쓰이는 정의라서 정리하고 간다. KL Divergence에 대한 수학적 분석은 나중에 다른 포스팅(따로 정리하고 있는 정보 이론 시리즈에서 더 자세하게 다룰 예정)에서 이어가도록 하고 여기서는 이런 방법론도 있다 정도만 짚고 넘어간다.

Optimization

Loss는 모델이 얼마나 잘 예측했는지를 판단하기 위한 메커니즘이었다면 optimization은 판단한 근거를 가지고 어떻게 가중치를 업데이트 시키는 지에 관한 것이다.

Optimization이라고 하는 것은 특정 조건에 대해서 이를 만족하는 가장 최적의 elements 값들을 찾는 과정이다. 이를 위해서 많은 아이디어들(랜덤하게 찾기, 하나씩 다 대입해보기 등)이 있지만 가장 흔히 사용되는 기법은 바로 Gradient 를 이용하는 것이다.

Gradient

Gradient(미분)이란 곡선 위에 한 점을 찍고, 그 점에서 가장 곡선에 근접한 직선(best linear approximation)을 찾는 것이다.

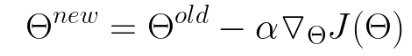
loss function에 대해서 미분하여 그 반대(-) 방향으로 업데이트 시키는 방법이다. 반대 방향인 이유는 아래와 같은 볼록 함수를 보면 기울기의 반대 방향으로 이동해야지 최저점(Loss가 가장 작은 지점)으로 갈 수 있기 때문!

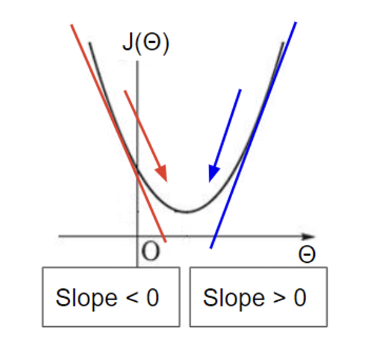
하지만 이렇게 기울기(gradient)만 찾아서 최적점을 찾기에는 문제점들이 있다.

곡면이 convex 하지 않을 수 있다 → Local optima 나 saddle point 가 있을 수 있다는 말! 다른 말로 하면 기울기는 0이지만 그게 global optima라는 보장은 없다.
cost function(loss function)이 미분 가능하다는 전제가 있어야 한다.
local minimum으로 수렴하면 속도가 상당히 느려진다.

이를 해결할 수 있는 방안이 바로 이 gradient에 stochastic 요소를 추가하는 것이다.

Stochastic Gradient

mini batch 개념을 도입하여 하위 집합에 대해서 loss를 계산하여 업데이트 하는 방식이다. 이전 방식은 예를 들어 샘플이 1000개가 있다면 전체에 대해 하나씩 로스를 계산하는 것이었다면, 이번에는 특정 개수(32, 64, 128…)씩 랜덤하게 추출해서 데이터를 쭉 보고 한번에 로스를 계산하는 것이다.

이렇게 하면 속도도 빠르고 local optima에 빠질 확률도 덜 하다. 하지만 mini batch 크기 만큼 올려놓고 모델을 돌리는 것이기 때문에 메모리 소모가 있어 컴퓨터 사양 등에 따라 batch 크기를 정해야 한다.

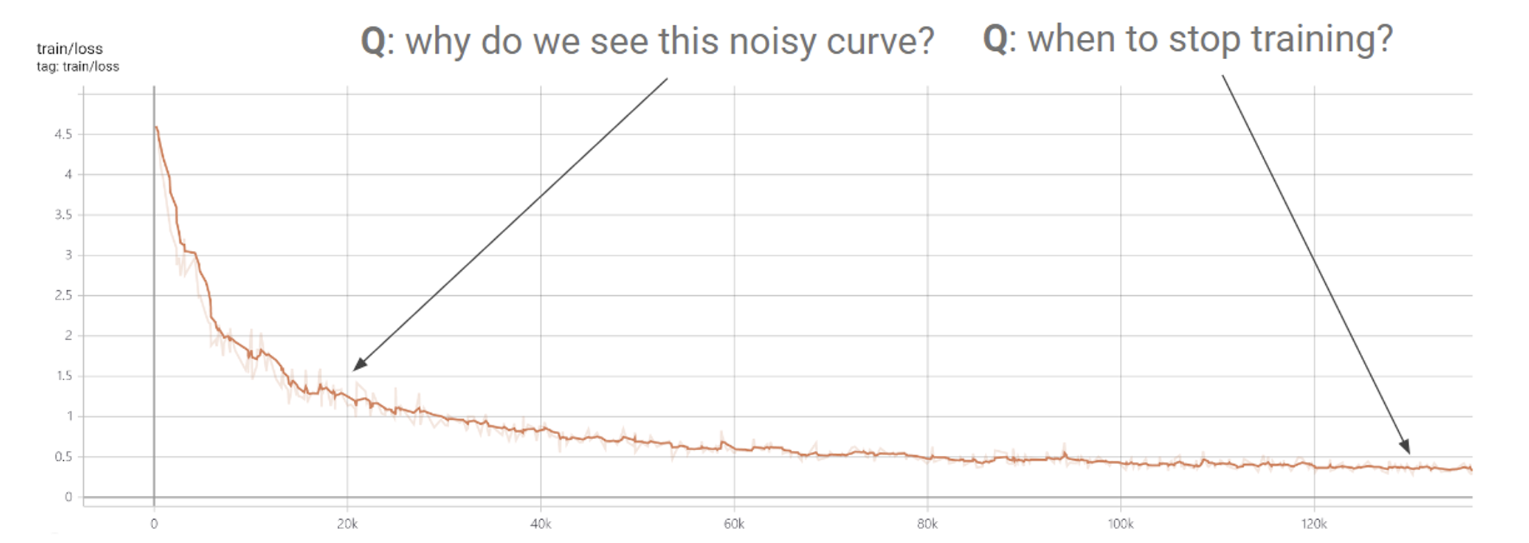
이렇게 train loss를 구해보면 smooth 하지 않고 noisy 하게 나온다. 그 이유는 바로 stochastic 하기 때문. 랜덤으로 mini batch 사이즈만큼 샘플링을 하고 로스를 계산하는 것이므로 일정한 방향으로 로스가 계속 감소하는게 아니라, 어떨 때는 다시 올라가기도 한다. 따라서 언제 train을 멈춰야 하는지 잘 고려해서 알고리즘을 짜야 한다.

Cross Validation

테스트 셋은 어떠한 경우에도 모델에게 노출시키면 안되므로 꼭 따로 빼두기. 이때 테스트 셋은 랜덤하게 10~20%로 나눠서 따로 저장할 수도 있고, 미래의 데이터를 바로 테스트 셋으로 사용할 수 있다.

추가로 validation set 을 따로 뺀 후에 이를 hyperparameter 를 튜닝하는 데에 사용한다.

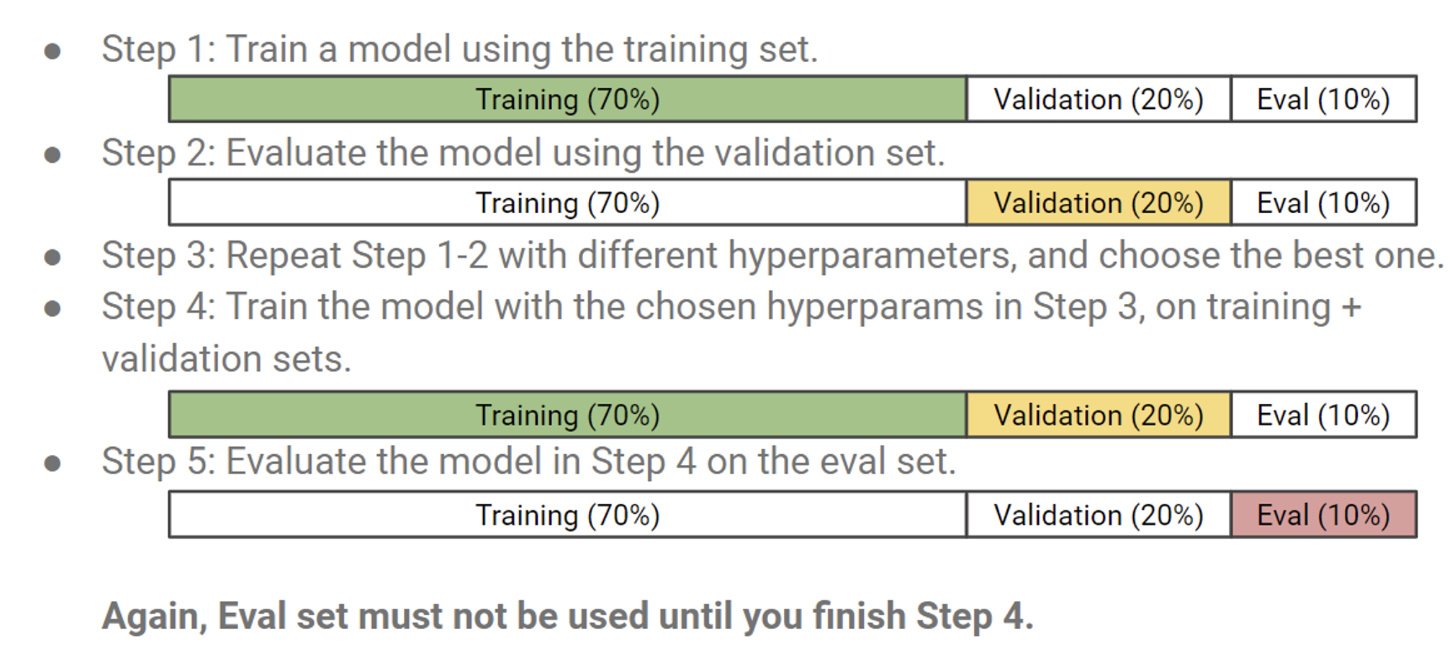
여기서 step4는 optional 하다. 모델 선정을 마쳤다면 따로 뺐던 20%의 validation set 도 함께 train을 시켜버리는데, overfitting의 위험이 올라가긴 하지만 성능이 향상될 것이기에 사용하는 경우도 많다.

여기까지 Loss function & Optimization 방식에 대해 기초적인 내용을 다루었다. 물론 이것 외에도 상당히 많은 loss function이 존재하며, 최근에 진행하는 한블리 프로젝트에서는 custom loss function으로 직접 만들어서 사용하고 있기도 하다. 그럼 오늘 포스팅은 여기까지~🤩