이준석 교수님의 유튜브 강의 Lec2 First approaches for image classification 영상을 참고해서 정리한 내용입니다. 다른 출처표기가 없는 이미지는 유튜브 영상에서 가져온 것임을 밝힙니다.
https://www.youtube.com/watch?v=FHRkxoF9nl0

Challenge of CV

생각을 해보자. 인간은 이미지를 보면 시각 외에 정보들(기억, 경험 등)을 이용해서 이 이미지 속 물체가 무엇인지를 판단할 수 있다. 무엇보다 인간은 intuition이 있기 때문에 “그냥 느낌이 이런데?” 식으로 직감으로 때려맞추기가 가능하다.

하지만 컴퓨터가 바라보는 이미지는 그냥 숫자값들이 나열된 텐서일 뿐. 그말은 즉 RGB 수치가 조금이라도 변화가 생기거나 한다면 컴퓨터는 그 이미지의 정체를 알아내는게 쉽지 않다.

고양이 사진을 분류한다고 생각을 해보자. 이미지 중심에 고양이 얼굴이 크게 보이도록 하고 배경이 단조롭다면 인간이나 컴퓨터나 “이거 고양이 사진이네”라고 비교적 쉽게 판단할 수 있을 것이다. 하지만 고양이 궁댕이 사진이라면? 인간이야 바로 여전히 고양이 사진이라고 답할 것이지만 컴퓨터는 순식간에 바뀌어버린 픽셀값에 혼란이 오고, 고양이라는 정보를 얻지 못할 가능성이 높아지게 된다.

그럼 고양이가 화면 가장자리에 작게 들어가있으면 어떨까? 혹은 배경이 다른 사물로 가득 채워져 고양이가 상대적으로 잘 안보인다면? 고양이의 전체가 아닌 일부만 보인다면? 이런 variation이 있는 이미지에 대해서도 컴퓨터가 일관성 있는 결정을 내리기 위해서는 많은 challenge가 있다.

Approaches

image classification의 challenge를 해결하기 위한 시도들

1) 배경 분리하기

edge 찾기 → bit map 구성 → 형태를 찾기

이러한 방식은 당연히 모두 fail, 고양이가 고개만 돌리면 게임 끝이다. 초반에는 연구가 활발했지만 뒤로 갈수록 사용하지 않는 방법이 되었다.

2) Machine Learning 이용하기

💡 갑자기 든 의문.. 머신러닝이란 뭘까?

인공지능, 딥러닝, 머신 러닝.. 요즘 다 혼용해서 사용하고 있는 단어들이기도 하고, 최근에 누군가 “딥러닝 아니고 머신러닝만 공부했었어요~”라는 이야기를 듣기도 했다. 그러다보니 자연스레 뭐가 뭔지 궁금했는데 마침 개념 찝어주시는 김에 정리를 좀 해보기로.


1) 머신러닝
데이터를 분석하고, 데이터로 부터 학습한 다음, 학습한 것을 적용해 정보에 입각한 결정을 내리는 알고리즘을 포함한 인공 지능의 애플리케이션. 결국 데이터를 통해 학습하고, 학습한 것을 토대로 새로운 데이터에 적용하는 것을 말한다고 정리할 수 있다. Supervised Learning을 생각하면 될 것 같다.
2) 딥러닝
알고리즘을 계층으로 구성하여 자체적으로 배우고 똑똑한 결정을 내릴 수 있는 인공 신경망을 만드는 것.
여기서 인공 신경망이란 자체적으로 배우고 지능적인 결정을 내릴 수 있는 알고리즘으로, 이를 여러 계층으로 구성한 것을 딥러닝이라고 한다. 따라서 딥러닝은 머신러닝의 한 종류라 볼 수 있다.

참고: https://www.zendesk.kr/blog/machine-learning-and-deep-learning/

그럼 이제 Machine Learning으로 위 문제를 어떻게 해결하려고 하였는지 알아보자.

1) Nearest Neighbor

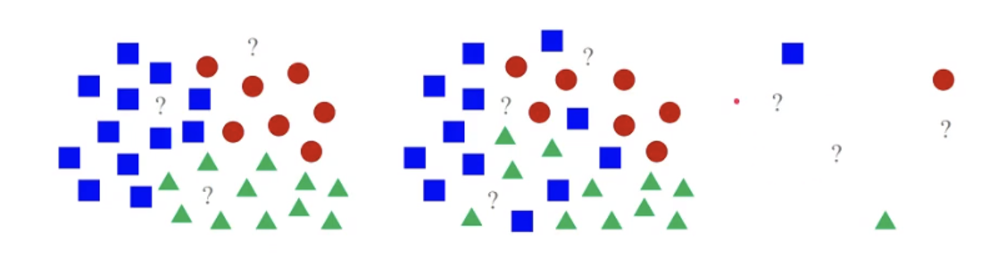
이미지 분류에 있어서 가장 직관적인 해결 방안

위의 그림으로 설명해보자면 이러한 방식이다. 우선 모든 빨간 원, 파란 네모, 초록 세모를 다 저장을 해두고, 새로운 데이터가 들어오면 가장 가까이에 있는 모형으로 간주한다. 첫 번째 사진에서 물음표 자리에 새로운 데이터가 들어온다면 가장 가까이에 있는 모형으로 만들어주면 끝!

이미지 분류에서도 동일한 메커니즘으로 작동한다.

train에서 모든 이미지-라벨 쌍을 저장한다. 후에 inference에서 새로운 이미지가 들어오면 가지고 있는 데이터를 쭉 훑어 보면서 가장 가까운(비슷한) 이미지를 찾고 라벨을 동일하게 붙이면 되는 방식.

Similarity of Images

이때 두 이미지가 서로 얼마나 비슷한지는 어떻게 계산할까?

앞서 말했듯 결국 이미지는 RGB 값으로 이루어진 행렬이다. 두 이미지 사이의 유사도를 정확히 표현하긴 힘들지만 두 행렬의 유사도(거리)는 이미 수식으로 잘 정리되어 있으니 그걸 이용하면 된다.

1. L1 Distance(Absolute Difference)

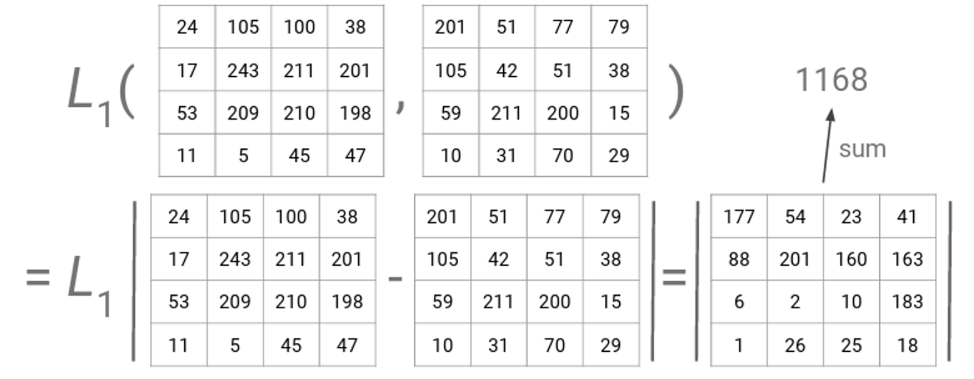
두 행렬의 크기가 같다고 가정하고, 각 원소끼리의 차를 구한 후 절댓값을 씌워주면 된다. 두 행렬이 완전히 동일하다면 L1 Distance = 0이 나올 것이며 다르면 다를 수록 0보다는 큰 값이 나올 것이다.

2. L2 Distance(Squared Difference)

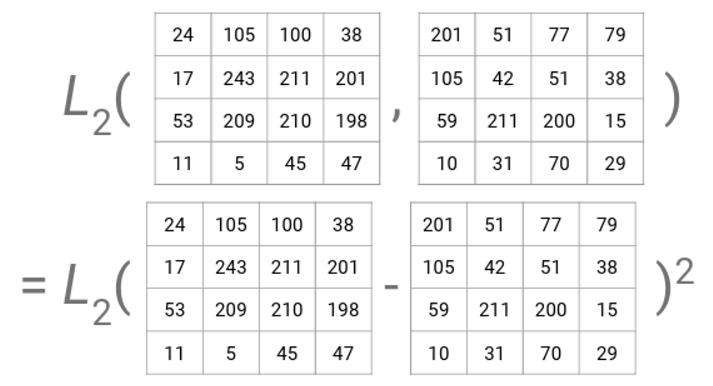
이번에는 원소끼리의 차를 구한 후 절댓값 대신 제곱을 한 후에 루트를 씌우는 방식이다. 사실 L1과 다를 게 없지만 차이점이라고 하면 여기서는 제곱을 하기 때문에 차이가 크면 클 수록 더 큰 차이를 만든다는 것 정도가 있을 것 같다.

그럼 이제 L1 Distance를 이용해서 Nearest Neighbor Classifier 코드 스니펫을 짜보자.

import numpy as np

class NNClassifier:
	def __init__(self):
		pass
	
	def train(self, images, labels):
		# Save all the training data
		# Time Complexity - O(1)
		self.images = images
		self.labels = labels
	
	def predict(self, target_image):
		minD = MAX_VALUE
		
		for i in range(images.shape[0]):
			# L1 Distance
			# Time Complexity - O(N)
			distance = np.sum(np.abs(self.images[i, :] - target_image))
			
			if distance < minD:
				minD = distance
				min_idx = i
		
		return self.labels[min_idx]
				

• Train 과정에서 Time Complexity가 O(1)인 이유는 이미 다 끌고 온 이미지와 라벨 데이터를 매핑만 시켜주는 것이기 때문. 물론 끌고오는 과정까지 생각한다면 O(N)이 맞다.

위 time complexity를 보면 별로 좋지 못한 알고리즘이라는 걸 알 수 있다. 생각해보자. train은 오래 걸려도 한 번 해놓고 저장해놓으면 되는 거라 큰 상관이 없지만, inference에서 오래 걸린다면 새로운 데이터를 마주할 때마다 그만큼의 시간 소요가 필요하다는 말이다. 따라서 머신러닝에서는 그만큼 inference 단계에서의 시간 복잡도가 훨씬 더 중요하다는 말!

Decision Boundary

이번에는 Decision Boundary의 측면에서 생각을 해보자.

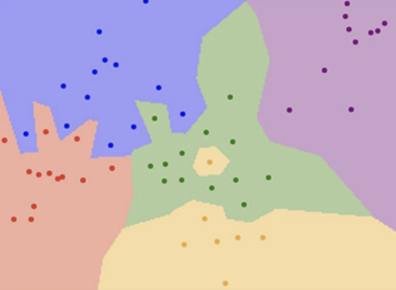
데이터 포인트마다 boundary가 만들어진다고 보자. 그럼 위 그림과 같이 복잡한 경계선이 생김과 동시에 “클래스 영역”이 만들어 진다. 그럼 새로운데이터가 어느 영역에 속해있는지 판단하면 바로 클래스 분류를 할 수 있다.

근데 이런식으로 하면 문제점은 바로 위 그림의 중앙에 있는 노란색 영역이다. 노란색 포인트가 하나 초록색 영역에 섞여들어가면서 작은 노란 섬(?) 하나를 만들어버렸다. 당연히 실제 데이터는 훨씬 더 많은 노이즈를 가질 것이기 때문에 그럼 결과적으로 훨씬 더 뒤죽박죽 섞인 경계선들이 만들어 질 것이다.

이를 해결하기 위해서 등장한 K-Nearest Neighbor Classifier

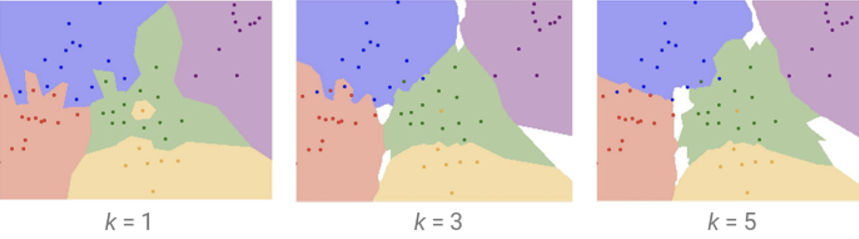
가장 가까운 데이터 포인트 하나에만 의존하지 말고, K개의 데이터 포인트의 다수결로 라벨링을 하는 방식이다. K=3이라는 것은 새로운 데이터와 가장 가까운 3개의 데이터 포인트를 보고 그 중 다수결의 라벨과 동일한 것으로 라벨링 한다는 의미가 된다.

하지만 동시에 문제점은 위 그림 상에서 보이는 하얀 부분. 바로 “분류 불가능한 영역”이 된다. 생각을 해보자. 새로운 데이터가 들어왔는데 가장 가까운 3개의 데이터를 봤더니 다 다른 라벨을 가지고 있었다고 치자. 그럼 이 데이터포인트는 어느 하나의 클래스로 분류할 수 없게 된다. 그리고 당연히 k 값이 클수록 하얀 영역, 즉 분류 불가능한 영역의 범위는 커지게 된다.

그럼 k값은 어떻게 고르면 될까?

뭐 사실 대부분의 머신 러닝에서 그렇듯 여기서도 해답은 결국 Trial and Error다. k=1, 3, 5 … 등 여러 값으로 훈련을 시켜보고 가장 정확도가 높은 k값을 선택하면 된다.

Limitation

사실 k-Nearest Neighbors는 거의 쓰이지 않는데 바로 다음과 같은 문제들 때문이다.

1. Distance metric

   사실 픽셀 값의 거리를 측정하는 방식은 그리 유용한 방식이 아니다. 예를 들어 아래와 같은 원본 사진에 세 가지 variation을 줬다고 하자.

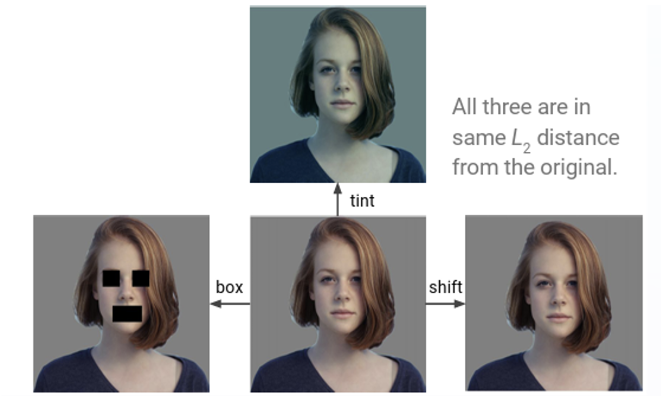
box는 사진 일부에 마스킹 처리를, tint는 색 보정을, shift는 픽셀 값을 한 개씩 미룬 사진들이다. 우리의 눈으로 봤을 때 shift에는 아무런 차이가 없으며 tint는 색이 변하긴 했다만 여전히 원본과 유사한 사진이 될 테고, box는 원본과 가장 큰 차이를 보이는 이미지라 판단할 것이다.
하지만 컴퓨터의 입장에서는 세 변형된 이미지는 모두 원본과 L2 Distance가 같은, 동일한 유사도를 가진 사진들이다. 그렇기에 인간이 생각하는 “유사도”와는 상당한 차이를 보인다.

2. 앞서 말했듯 inference가 굉장히 느리다.
3. 가장 큰 문제인 Curse of Dimensionality.

한국말로 하면 “차원의 저주”. 쉽게 생각해보면 차원이 크면 클 수록 그에 맞게 데이터가 많이 필요하다. 1차원과 3차원을 생각해보자. 1차원에서 점이 4개 있는 것과 3차원 공간에 점이 4개 있는 상황을 생각해보면 후자에서 점들 사이의 거리가 훨씬 멀어질 것이다. 이 상황에서 차원이 더 늘어나면? 우주에 둥둥 별 하나씩 떠다니는 느낌이 되지 않을까.

이렇게 되면 가장 가까운 k개와 동일한 라벨링을 하는 Nearest Neighbor Classification이 의미가 점점 사라진다.

2) Linear Classifier

앞서 봤던 Nearest Neighbor Classifier의 경우에는 train 단계에서 모든 이미지-라벨 쌍을 암기하기만 했다. 이번에는 단순히 몽땅 암기해버리는 것이 아니라 주어진 데이터를 학습하고 이를 기반으로 새로운 데이터에 대해 예측하는 모델을 보자.

입력으로 이미지 x가 주어지면 우리는 클래스 y로 매핑을 해야 한다. 이때 x를 y로 매핑하는 함수 f를 잘 학습하면 어떤 데이터가 들어와도 가장 그럴싸한 특정 클래스로 매핑해주지 않을까?

우선 f 중에서도 가장 간단한 함수인 linear function부터 보자.

파란색이 이미지 픽셀에 해당하는 값들을 나타낸 행렬이고, W가 바로 weight 행렬이다. 이때 “파라미터” 혹은 “가중치”는 모델이 학습해야 하는 값들이라 볼 수 있다. Linear function에서는 이미지가 들어오면 크기가 동일한 W 행렬와 함께 weighted sum을 구한다. 이때 weighted sum은 동일한 위치의 원소들끼리 곱한 후 다 더하는 것을 말한다. 그럼 딱 하나의 값이 나올 것이며, 그건 한 클래스에 대한 score이라 볼 수 있다.

이때 클래스가 1개가 아니라 10개라면?

그럼 동일한 크기의 W 행렬이 10개가 존재할 것이며 각각은 클래스에 따른 특징들을 잘 묘사하는 행렬이 될 것이다.

💡 각 클래스를 잘 묘사하는 W 행렬이 무슨 말일까?

예를 들어 클래스에 비행기가 있다고 하자. 그럼 대부분의 사진들은 하늘에 나는 비행기 사진이 있을 것이다. 즉 많은 이미지는 배경에 하늘색이 많이 나타날 것이고, “비행기”에 해당하는 W 행렬은 이러한 특징을 잘 반영하는 값들로 이루어져 있을 것이다. 따라서 클래스에 따라 각각의 W행렬이 있으며 각각은 해당 클래스의 특징을 잘 드러내는 값들로 채워져있을 것이다.

따라서 입력으로 이미지가 들어오면 각각의 W 행렬과 weighted sum을 한 후에 가장 값이 높은 클래스로 매핑이 될 것이다.

수식을 통해 차원을 한 번 계산해보자.

입력으로 들어온 이미지를 32 x 32 x 3이라고 하면 결국 하나의 이미지에 3072개의 숫자가 들어있는 것과 동일하다.

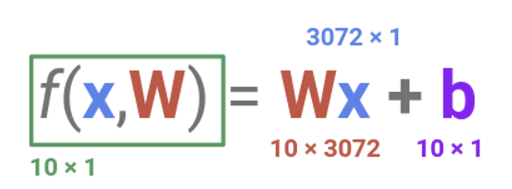
클래스가 10개라면 W는 10 x 3072의 차원을 가진다. 즉, 이미지와 동일한 크기의 행렬이 클래스마다 1장씩, 총 10장 있다고 생각하면 쉽다. 여기서 눈여겨 볼 것은 바로 보라색으로 표시된 b이다. 이게 무엇이며 왜 필요할까?

가장 간단하게 일차 함수를 생각해보자.y절편이 없다면 모든 일차 함수는 원점을 지난다. 하지만 y절편 값이 무엇이냐에 따라서 함수는 자유자재로 움직일 수 있다.

여기서도 동일하다. b는 bias, 편향이라는 의미로 데이터에 의존하지 않고 기본값으로 특정 값을 더해준다는 의미가 된다. 예를 들어 10개의 클래스 중에 강아지, 고양이 사진만 엄청 많다고 생각해보자. 그럼 모델이 바라보는 세상은 강아지 고양이가 넘치고 가끔씩 비행기나 배가 보이는 그런 세상일 것이다. 그렇다면 새로운 이미지가 들어오면 모델은 잘 모를 땐 강아지 고양이로 때려맞출 것이다. 인간이 그런 것 처럼!

그래서 bias term을 클래스마다 특정한 값을 가지도록 추가하여 이러한 편향을 잘 반영하도록 한다. 이는 데이터 입력에 의존하지 않는 값이며, 차원은 10 x 1이 된다.

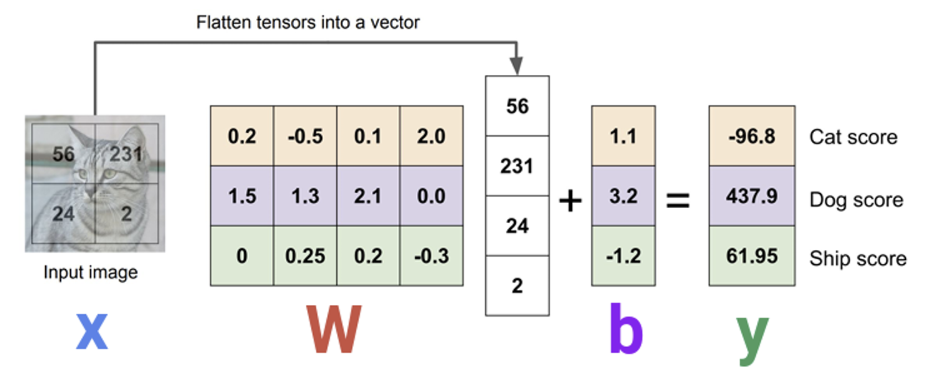
이 그림을 보면 Dog 클래스의 bias가 상대적으로 높다는 것을 알 수 있다. 이건 학습 과정에서 이미지 중에 강아지에 해당하는 이미지가 상당수였다고 추론해볼 수 있다.