[Generation] 1. Background(ELBO)

Understanding Diffusion Models: A Unified Perspective (Calvin Luo) 글을 바탕으로 공부한 내용입니다. 따로 출처 표기가 없는 사진, 수식은 위 자료를 출처로 합니다.
https://arxiv.org/abs/2208.11970

The Goal of Generative Model

특정 분포으로 부터 관측된 샘플 x가 주어졌을 때, 실제 데이터 분포인 $p(x)$를 모델링하는 것을 학습하는 것을 목표로 한다. $p(x)$가 학습된 후에는 이를 이용해서 새로운 샘플들을 생성할 수도 있다.

Plato’s Allegory of the Cave

우리가 관측할 수 있는 데이터는 latent variable z 로 부터 표현되거나 생성되었다고 볼 수 있다. 그렇다면 우리가 관측할 수도 없는 이 random variable z 는 무엇일까?

플라토의 동굴 우화 예시를 보자.

Painting of Plato’s “Allegory of the Cave” https://images.app.goo.gl/CFTS9HCxTcC75s8c9

사람들은 벽 뒤에 사슬로 묶여 벽만을 바라볼 수 있으며, 벽 뒤로는 불이 켜져 있다. 이때 불 앞에 어떤 3차원 물체가 있으면 사슬에 묶인 사람들은 오직 2차원으로 벽에 투영된 그림자만을 볼 수 있다. 3차원 물체가 무엇인지에 따라서 투영된 그림자는 달라지며, 사슬에 묶인 사람들은 그림자만을 이용해 물체를 추론하고 추측할 수 있다.

이와 동일하게 우리가 현실 세계에서 관측할 수 있는 데이터는 어떤 고차원의 함수로 부터 생성된 것일 수 있다. 2차원 그림자를 관찰하여 3차원 물체를 추론하는 것처럼, 우리도 관찰할 수 있는 데이터를 통해 더 고차원의 latent representation 을 추론할 수 있다는 관점이다.

하지만 여기서 주의할 점은, Plato의 우화화는 반대로 Generative modeling을 할 때는 저차원의 latent representation 을 찾도록 학습한다. 고차원은 강력한 prior가 없다면 큰 의미가 없기 때문에 저차원의 latent를 일종의 compression(압축) 으로 간주하여 학습하고자 한다.

1-1. Evidence Lower Bound(ELBO)

수학적으로 봤을 때, 관찰 가능한 데이터와 latent 변수들은 joint distribution $p(x, z)$로 모델링할 수 있다. Generative modeling의 접근 방식 중 likelihood-based 방식은 모든 관찰된 x에 대해 likelihood $p(x)$를 최대화하도록 모델을 학습시키는 것이다. \

그럼 z와 x가 joint로 엮여있는 상황에서 $p(x)$는 어떻게 구할까?

🟡 Equation 1: marginalize

Joint probability에서 x의 probability를 구하고자 한다면 $p(x, z)$에서 모든 latent variable z에 대해서 적분하여 구할 수 있다.

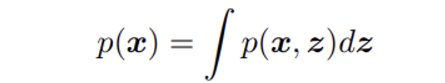
🟡 Equation 2: chain rule of probability

조건부 확률을 이용한 chain rule로 구하는 방법이다.

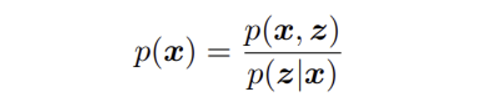
하지만 $p(x)$를 바로 구하는 것은 상당히 까다롭다.

marzinalize에서 모든 latent variable z에 대해 적분하는 계산이 복잡할 뿐더러, chain rule of probability 에서는 실제 latent 인코더 $p(z|x)$에 접근할 수 있어야 하기 때문이다.

따라서 x의 likelihood를 구해서 최대화하는 것은 상당히 복잡하지만, 대신에 위 두 방정식을 이용하면 Evidence Lower Bound(ELBO)를 구할 수 있다. 이는 evidence 의 lower bound 를 의미한다.

여기서 evidence는 관측된 데이터의 log likelihood를 의미힌다.

📌 Evidence는 “증거”라는 뜻으로, 주어진 데이터가 주어진 모델에서 발생할 확률에 대한 증거를 나타내는 용어다. 확률 이론에서 Evidence는 결국 특정 가설이나 모델이 관찰된 데이터와 얼마나 일치하는지를 나타내는 개념이다.

따라서 여기서 evidence는 관찰된 데이터의 log likelihood로 수치화할 수 있다고 말하고 있다.

즉, ELBO는 $p(x)$의 하한선을 정의하고 있으며, 특성상 $p(x)$를 바로 최대화하기 어렵기 때문에 하한선 ELBO를 대신해서 최대화하려고 한다.

What is ELBO?

그럼 ELBO가 무엇이며, 어떻게 $p(x)$를 대신해서 최적화할 수 있는지 알아보자.

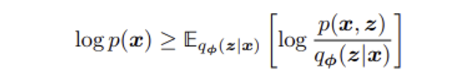
여기서 부등식 오른쪽 항이 바로 ELBO 수식이다. 위의 방정식은 ELBO가 $p(x)$의 하한선임을 정의하고 있다.

여기서 $q_\phi(z|x)$는 파라미터 $\phi$에 대한 근사적인 variational distribution (변분 분포)을 의미한다. 이때 variational distribution은 “찾고자 하는 분포를 근사하는 데에 사용되는 분포”라고 이해하면 된다. 즉, 우리가 찾고 싶은 것은 $p(z|x)$이지만 앞서 말했듯 이는 latent encoder에 대한 접근이 필요하기 때문에 우리는 파라미터 $\phi$를 이용하여 이에 접근하고자 한다.

그럼 여기서 왜 우리가 ELBO를 최대화하려고 하는지 알아보자.

Jensens’s Inequality를 이용하여 ELBO가 $p(x)$의 하한 값임에 도달할 수 있다.

📌 Wiki를 참고하면 볼록 함수를 $\phi$라 할 때 다음 부등식이 성립한다.

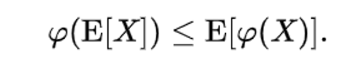
이때 log는 오목함수(아래로 볼록한 함수)이기 때문에 부등호 방향이 반대로 바뀐다. 이를 적용하면 식(8)을 도출할 수 있다.

하지만 아직까지 우리가 ELBO를 최대화해야 하는 이유를 설명하기에는 부족하다. 이번에는 Equation 2를 적용하여 ELBO를 도출해보자.

식 (15)를 눈여겨 보면 결국 Evidence = ELBO + KL Divergence $(q_\phi (z|x) ||p(z|x))$가 된다.

KL Divergence

📌 KL Divergence란?

Kullback-Leibler divergence(KLD)는 두 확률 분포의 차이를 계산하는 함수로, 특정 분포를 다른 분포로 근사했을 때의 정보 손실을 나타낸다. 여기서 말하는 두 분포의 차이는 정확히 말하면 정보량의 차이를 뜻한다.

$D_{KL}(P||Q)$는 확률분포 P를 기준으로 확률분포 Q에 근사했을 때 발생하는 정보량 차이라 볼 수 있다. 이때 $D_{KL}(P||Q) \neq D_{KL}(Q||P)$이며, KL Diverce는 항상 음수가 아닌 값을 가진다.

KL Divergence에 대해서 자세히 정리한 글이 있으니 참고하면 도움이 될 것이다.

다시 위의 수식을 해석하면 결국 Evidence는 ELBO에 실제 posterior과 추정된 posterior간의 정보량 차이를 더해준 것이라 볼 수 있다. 이 관계식을 이용하면 ELBO와 evidence 사이의 관계와 더불에 ELBO를 최대화하는 이유를 설명할 수 있다.

1. ELBO가 evidence의 하한값인 이유

Evidence = ELBO + KL Divergence이며 위에서 말했듯 KL Divergence는 항상 음수가 아닌 값을 가진다. 따라서 ELBO는 evidence보다 항상 작거나 같기 때문에 하한값이 될 수 있다.

2. ELBO를 최대화하는 이유

우리는 파라미터 $\phi$를 최적화하여 variational posterior $q_\phi(z|x)$를 최대한 true posterior $p(z|x)$와 비슷하게 만들고 싶다. 그러기 위해서는 둘 사이의 KL Divergence를 최소화해야 하지만, true posterior 값을 모르기 때문에 다이렉트하게 KL Divergence를 최소화하는 것은 불가능하다.

이때 식 (15)를 이용하여 약간의 트릭을 써보자.

좌항인 $\log p(x)$는 $\phi$에 대해서 constant 다. 결국 식 (15)는 상수 = ELBO + KL Divergence가 되기에 KL Divergence를 최소화 하는 것은 ELBO를 최대화하는 것과 동일하게 된다.


따라서 ELBO를 최적화할 수록 근사 posterior는 실제 posterior과 가까워지며, 이를 통해 evidence를 더 잘 근사할 수 있다는 것이다!