이번 글은 대학교 강의에서 공부한 내용을 바탕으로 정리한 글입니다. 출처가 없는 사진 자료는 강의 자료 ppt에서 가져왔음을 밝힙니다.

Variational Auto-Encoder, 줄여서 VAE라고 부르는 모델에 대해 알아보자.

Genertive model을 공부하면 항상 등장하는 이 다이어그램. 이번 포스팅에서는 그 중에서 VAE를 다룰 예정이다. 인코더-디코더 베이스로 된 이 모델이 어떻게 새로운 샘플을 생성하는지 알아보자.

Latent Variable

이미지를 보면 정말 다양한 features를 담고 있다. 가령 아래 이미지를 봤을 때 어떤 features를 가지고 있을까?

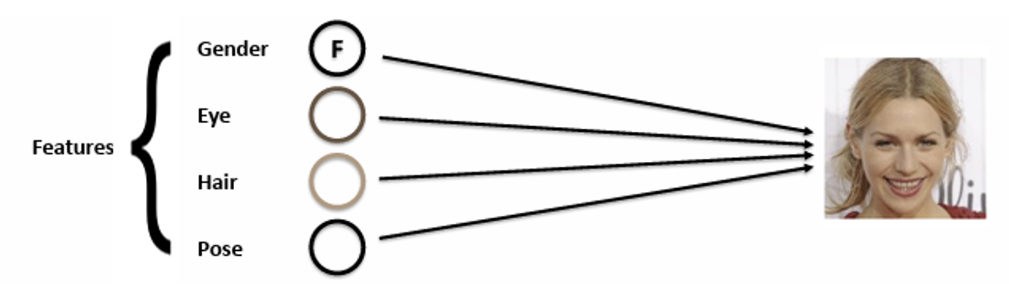
한 여자가 있고, 금발 머리에 갈매기 눈썹, 환한 미소 등.. 엄청나게 많은 features를 가지고 있다. 따라서 일일이 사람이 손으로 이러한 high level features를 구체화하는 것은 너무나 어렵다. 수백, 수천만장의 사진에 대해서 언제 모든 features를 하나한 다 구체화하고 있을 텐가?

그래서 우린 이러한 태스크를 위해 Deep Learning 모델을 도입했다.

새로운 벡터 z를 만들고 입력으로 들어오는 이미지에 대한 중요한 요소 들을 잘 표현하도록 훈련을 시킨다. 그럼 인간처럼 “눈 = 파란색”, “머리=금발” 등 하나 하나 features를 구체화하고 정리할 필요가 없다. 컴퓨터가 알아서 이미지를 집약적으로 표현하는 적절한 값들로 채워진 벡터를 생성할 것이니. 🤩

그럼 이제 남은 문제는 어떻게 z 벡터를 어떻게 만들 것이냐이다.

이 문제를 보니 NLP에서 어떻게 해야 word를 잘 표현하는 임베딩 벡터를 만들 것이지에 대한 문제를 해결하기 위해 word2vec이나 GloVe가 발명되었다는 이야기가 생각난다. 그때는 단어를 어떤 “숫자”들로 이루어진 벡터로 만들어야 해당 단어를 잘 표현할 수 있을까에 대한 고민이었다.

여기서도 사실은 동일하다. 우리가 하고 싶은 것은 이미지에 대해 어떤 “숫자”들로 이루어진 크기가 작은 벡터를 만들어야 이미지를 더 잘 표현할 수 있을까에 대한 문제다. 즉, unsupervised manner 에서 더 의미있는 임베딩 벡터를 만들고자 하는 것이다.

그에 대한 첫 번째 Approach가 바로 AutoEncoder 이다.

AutoEncoder

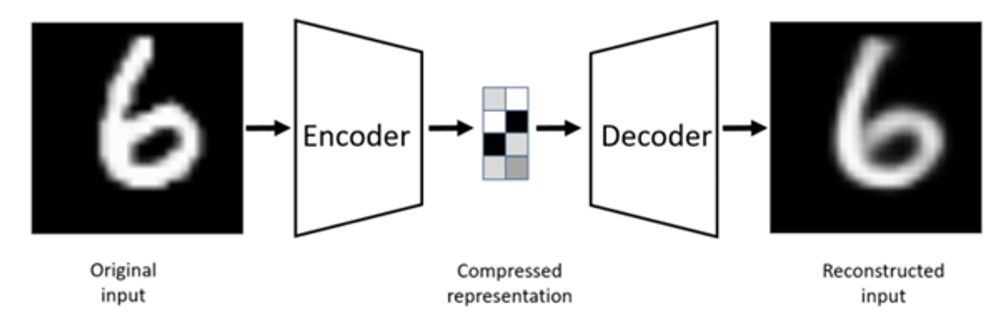
AutoEncoder는 unsupervised 상황에서 주어진 이미지를 low dimension representation으로 변환하는 것을 학습한다. 참고로 이러한 작업을 representation learning 이라 부르기도 한다.

• input: 라벨이 없는 데이터(이미지 등)
• intermediate: 차원이 작은 representation vector
• output: Reconstructed input

이때 z에 대한 가정이 없으며, L2 Loss를 이용하여 reconstruction error를 계산하여 이러한 손실을 줄이는 방향으로 학습한다.

사실 AutoEncoder는 재구성한 이미지를 얻는게 목적이 아니라, 이전에 말했듯 latent vector 를 더 잘 만들기 위함이다. reconstruction error가 낮을 수록 z 벡터는 입력 이미지를 잘 나타낸다고 간주한다.

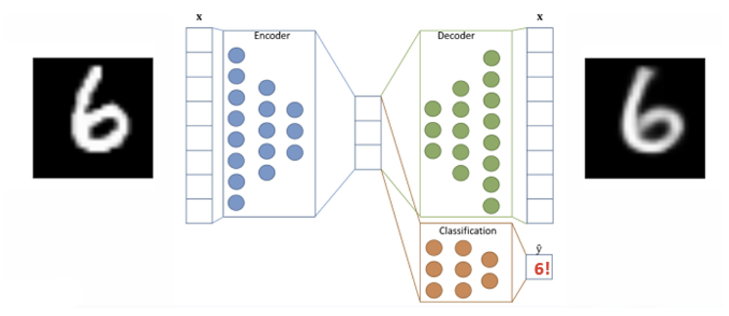
따라서 AutoEncoder를 훈련시키는 목적은 Encoder를 얻기 위함 이며, 훈련 후에 Decoder는 버리고 classifier 등 다른 downstream task와 연결 지어서 사용하는 경우가 대다수다.

여기서는 좋은 latent vector를 얻으면 끝이었지만 Generation 과는 완전히 다른 이야기다. “생성”으로 넘어가는 순간 사실 인코더보다는 디코더 가 중요하기 때문.

그럼 이렇게 잘 만들어진 AutoEncoder와 latent vector를 이용해, 잘 만들어진 decoder를 붙이면 새로운 이미지를 잘 생성할 수 있지 않을까?

VAE

AutoEncoder에 그대로 디코더를 붙여 새로운 샘플을 생성하고 싶지만 사실 바로 연결하는 것은 불가능하다.

이유는 이러하다.

1. P(z) 가 어떠한 분포를 가지는지 모른다.
2. 따라서 P(z) 에서 어떻게 샘플을 추출하는지 모른다.
   
   

흠. 결국 AutoEncoder에서 인코더를 잘 학습시켜서 입력에 대해 좋은 벡터를 생성해내는 것까지 해냈으나, 이 latent vector에 대한 분포를 모르다보니 디코더를 학습시킬 수 없었다.

따라서 여기서 우리가 취할 수 있는 해결방안은 바로 p(z)를 tractable 하게 만드는 것!

📢 왜 AE와 다르게 VAE에서는 z 의 분포를 알아야 할까?

그 이유는 AE와 VAE의 main purpose부터가 다르기 때문이다.

AE

• 좋은 인코더를 만드는 것이 목적
• 어떻게 하면 input data를 잘 표현하는 latent vector를 만들 수 있을지가 관건이며, 따라서 데이터를 잘 represent하는 차원이 작은 벡터를 만들고자 함
• 디코더의 역할은 결국 이 latent vector로 데이터를 복구했을 때 얼마나 원래 데이터와 다른지 계산하여, latent vector가 원래 데이터를 더 잘 표현하도록 만듦
• 따라서 학습이 끝나면 더이상 디코더를 떼버리고 latent vector 만드는 용으로 인코더만 사용하는 경우가 다수.

VAE

• VAE는 AE와 목적이 비슷하지만 다른 점이 바로 latent vector를 생성하는 과정에서 Stochasticity를 도입한다는 것
• AE에서는 입력 이미지에 대해 deterministic한 하나의 latent vector를 생성했다면, VAE에서는 latent vectors의 distribution을 생성한다.
• 입력 데이터에 대한 분포를 만들면 decoder에서 이 분포에서 sampling을 한 후 데이터를 reconstruct하는 방식.
• 이때 latent vectors z가 Gaussian 분포를 따른다면 인코더에서는 평균과 분산을 학습하여 각 입력 데이터에 맞는 하나의 분포를 생성
• 입력 데이터를 잘 표현하는 latent일 수록 평균(높은 확률)에 위치

따라서 위의 설명에 따르면 디코더에서는 z의 분포로 부터 샘플링을 하고 데이터를 생성해야 하기 때문에 z 의 분포를 아는 것이 매우 중요하다.

Train VAE model with ELBO

그럼 VAE를 어떻게 훈련시키는지 보면, 결국 likelihood를 최대화하는 방식으로 학습시킨다.

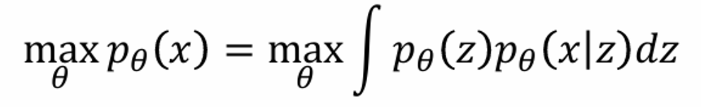
근데 이 VAE의 likelihood를 maximize하는 과정은 이전 포스팅에서 이미 잘 써논 듯 하니 Pass 하겠다.
수식과 전개 과정을 자세히 알기 위해선 꼭 위 포스팅을 참고하면 좋을 것 같다.

Reparameterization Trick

그런데 VAE의 학습 과정을 보면 하나의 문제가 있다. VAE의 학습 과정을 다시 예쁘게 정리를 해보자면 이렇다.

📌 VAE 학습 단계

1. 입력으로 데이터를 준다

2. 인코더에서 입력 데이터에 대한 latent vectors 분포를 구한다

   $p_\theta (z|x)$를 이용하여 latent space에 대한 가우시안 분포를 구한다.(이때 학습하는 파라미터 $\theta$는 가우시안 분포의 평균과 분산을 나타낸다)

3. Variational distribution(=Gaussian distribution)이 완성되었다!

4. 이 분포로 부터 샘플을 추출한다

5. 추출된 샘플을 디코더에 넣어서 새로운 샘플을 생성한다

그럼 여기서 문제는 바로 4번이다. 샘플링을 하는 순간 back propagation 연산이 불가능해진다는 것. 대신에 다른 트릭을 이용하여 미분 가능하게 만들어 한 번에 역전파가 가능하게 만들 순 없을까?

그래서 고안된 방법이 바로 Reparameterization trick 이다.

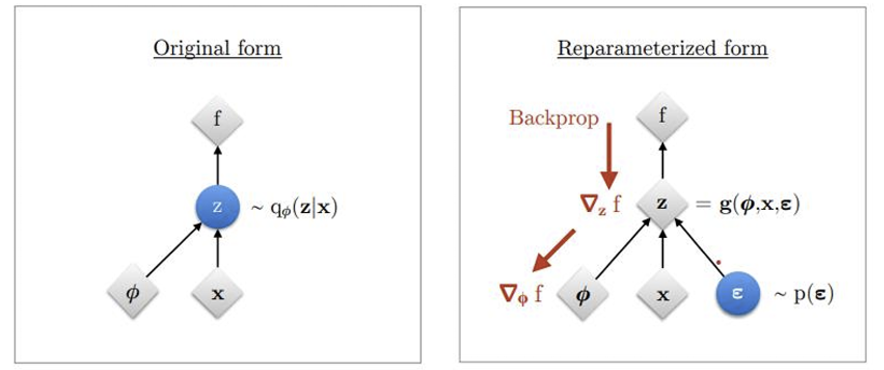
기존에는 왼쪽과 같이 입력 데이터에 대해 파라미터 $\phi$(여기서는 가우시안 분포의 평균과 분산)가 주어지면 바로 샘플링하는 방식이었다.

대신 이를 더 간단히 처리하기 위해 오른쪽과 같은 방법을 이용하고자 한다. 쉽게 설명하면 결국 미분이 가능해지게 만들기 위해서 바로 z 에서 샘플링하기 보다는 N(0, I) 에서 샘플링하여 scaling + translation을 시키자는 취지.

더 자세히 설명하면 이렇다.

1. $\epsilon$~N(0, I)일 때 엡실론을 샘플링한다.

2. $f = \Sigma \epsilon \ + \mu$

   샘플링 된 값에 분산만큼 scaling, 평만큼 translation을 시킨다.

그럼 결국 가우시안 분포에서 직접 샘플링한 것과 같은 결과를 낸다. 하지만 위의 경우에는 결국 엡실론에 대한 linear transformation이기 때문에 미분이 가능하게 되는 것이다.

$\beta$ -VAE

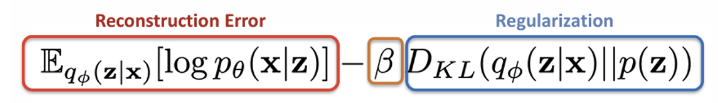
베타 VAE에서는 ELBO에서 딱 하나의 파라미터를 수정한 것이다. 바로 Regularization term에 베타 계수를 곱하는 것이다. 사실 VAE만 봤을 땐 모든 feature들이 entangled되어서 따로 분리할 수 없다.

하지만 이 features를 하나 하나 분리해서 보고 싶다면 뒤에 베타 항의 값을 키워주면 loss를 계산할 때 KL Divergence를 우선시하여 값을 낮춰준다. 따라서 두 분포 $q_\phi (z|x) , p(z)$를 서로 같게 만들어줘 features를 disentangled하게 만들 수 있다.

여기까지 기본적인 VAE에 관한 내용을 다루었다. 다음 포스팅에선 이어서 Normalizing Flow에 대해 정리 해보겠다. 🥰