드디어 Diffusion을 정리하는 첫 포스팅. 생성형 ai의 붐을 일으킨 장본인인 Diffusion 모델에 대해 정리해보자.

Diffusion

자 드디어 diffusion으로 왔다. 생성형 모델 중 현재 가장 hot한 diffusion 모델에 대해 공부해보자. 우선 Diffusion이란 무엇일까?

Diffusion은 실제 이미지에 t step에 걸쳐 노이즈를 조금씩 추가하는 방식이다. 이때 노이즈는 deterministic function을 이용하여 조금씩 원본 이미지에 추가한다. T step이 지나면 원본 이미지는 완전한 noise가 된다. 그럼 Diffusion 모델은 이러한 noise로 부터 노이즈를 조금씩 제거하여 이미지를 생성하는 방식으로 학습하는 모델이다.

Diffusion 방식을 활용한 많은 논문들이 있지만 가장 먼저 Denoising Diffusion Probabilistic Models를 알아보자.

---

DDPM

📖 Paper: https://arxiv.org/abs/2006.11239

👩‍💻 Ref blog: https://lilianweng.github.io/posts/2021-07-11-diffusion-models/

Diffusion은 forward diffusion process와 reverse diffusion process로 나뉜다. forward 는 실제 이미지에 노이즈를 추가하는 과정을, reverse 는 반대로 완전한 노이즈로 부터 노이즈를 조금씩 제거하는 과정을 나타낸다.

Forward Diffusion Process

Forward Diffusion은 원본 이미지에 노이즈를 조금씩 추가하는 방식이다. 다음 전개식은 $x_0$(원본 이미지)에서 $x_T$(완전한 노이즈)로 가는 transition 함수를 deterministic하게 정의한 것이다.

위 식은 $x_{t-1}$가 주어졌을 때 $x_t$로 딱 한 step에 대한 transition 식이다. 하지만 앞서 말했 듯 Forward Process 는 deterministic한 함수의 연속이다. 그렇다면 $x_0$, 즉 실제 real world 이미지가 주어졌을 때 time step t 번째 샘플을 얻을 수 있다.

이를 수학적으로 풀어보면 다음과 같다 .

즉, 위 처럼 식을 전개하면 x0에서 바로 내가 샘플링하기를 원하는 xt의 샘플을 얻을 수 있다.

Gaussian Smoothing

위에서는 x0가 주어졌을 때 xt를 구하는 방식에 대해서 논했다. 그럼 이번에는 $q(x_t)$를 다이렉트하게 구할 수 있을까?

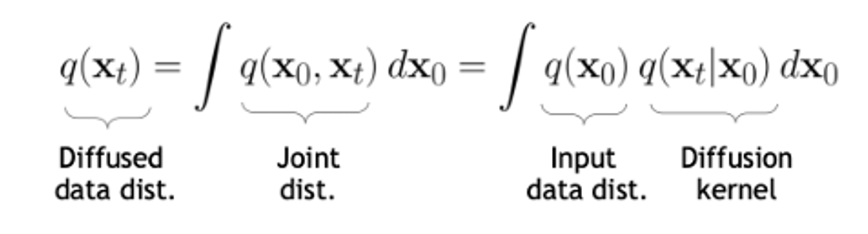
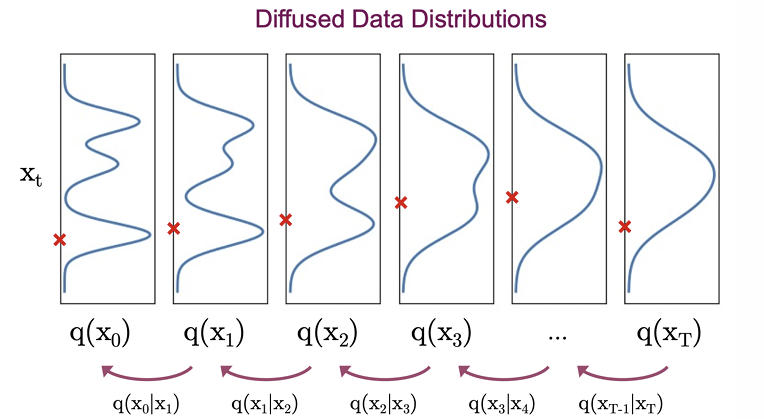
위 식처럼 결국 $q(x_t)$의 diffused data의 분포는 input data의 분포와 diffusion kernel의 분포를 곱한 것으로 부터 구할 수 있다.

따라서 결국 원본 데이터로부터 완전한 노이즈로 가는 forward diffusion process를 일종의 gaussian smoothing 과정이라고 볼 수 있다.

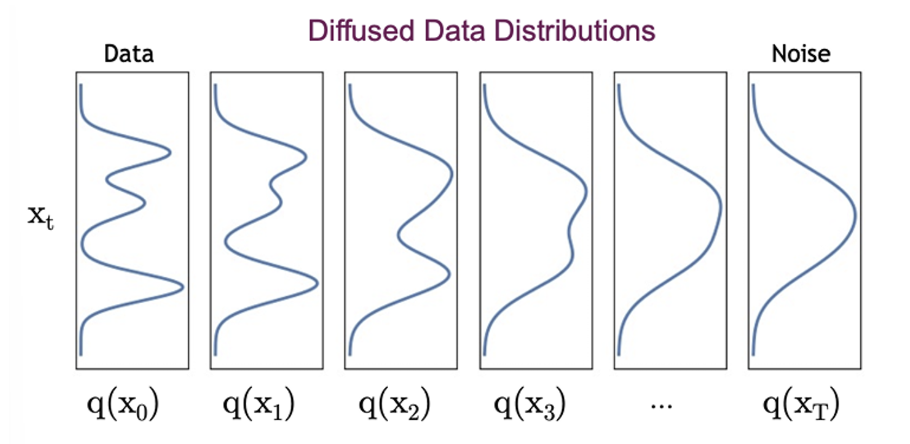
복잡한 분포로 부터 작은 노이즈를 점차 더해가면서 최종적으로는 간단한 가우시안 분포를 띄게 만들고 있다.

물론 이를 이용하면 reverse diffusion process까지 정의할 수 있다.

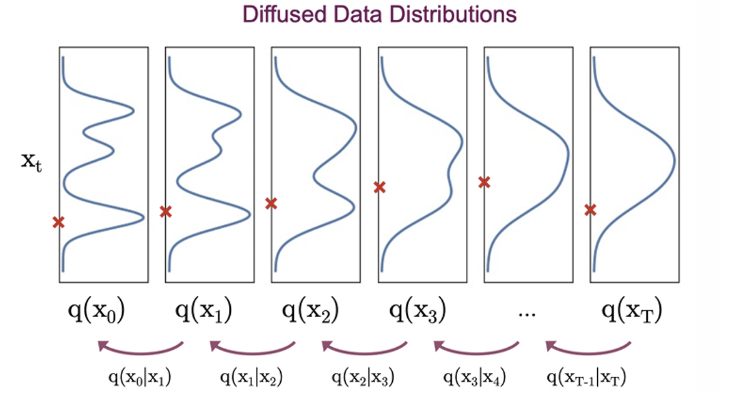
이번에는 완전한 가우시안 노이즈인 $q(x_T)$에서 부터 실제 이미지 분포로 매핑하는 과정이다. 여기서는 앞선 forward와 반대로 $q(x_{t-1}|x_t)$를 곱해 최종적으로는 $q(x_0)$을 구해야 한다.

⭐ 하지만 문제는 $q(x_{t-1}|x_t)$를 계산하는 것이다.

$q(x_{t-1}|x_t) = { q(x_{t-1})q(x_t|x_{t-1}) \over q(x_t)}$에서 사실 $q(x_t), q(x_{t-1})$을 계산하는 것은 매우 복잡하다. ($x_0$부터 $x_t$까지 차례대로 인테그랄로 계산해야 하는데 너무 복잡하기에 intractable하다)

따라서 이를 추정할 수 있도록 $p_\theta(x_{t-1}|x_t)$를 둬서 $q(x_{t-1}|x_t)$에 근사하도록 만드는 파라미터를 찾는 방향으로 디퓨전 모델을 학습시킨다.

Train Diffusion Models

Diffusion model의 최종 loss는 다음과 같다.

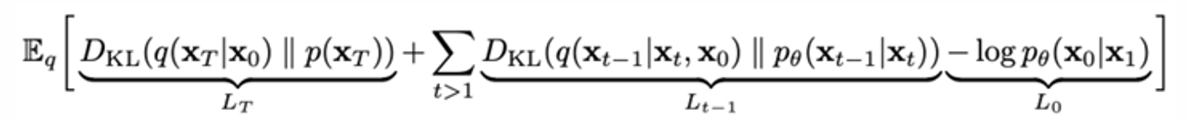
이는 Variational upper bound를 통해 얻을 수 있는데, 최종 loss를 구하는 과정은 생략하겠다. 지금 loss를 보면 크게 세 가지 항으로 나눠져 있으니 각각을 알아보자!

1) $L_T$

$L_T$는 $p(x_T)$와 $q(x_T||x_0)$ 사이의 KL divergence

하지만 prior인 p(x_T)는 standard gaussian dist를 따르며, q 또한 그렇기 때문에 둘 사이의 차이는 거의 없다. 따라서 KL divergence가 거의 0에 수렴할 정도로 작기 때문에 전체 loss에서 무시된다.

2) $L_{t-1}$

이번에는 $x_{t-1}$에 대해 p와 q의 분포 값이며, 이미 정의된 수식을 이용하여 KL divergence를 계산해보자.

$q(x_{t-1}|x_t, x_0)$

$p_\theta(x_{t-1}|x_t)$

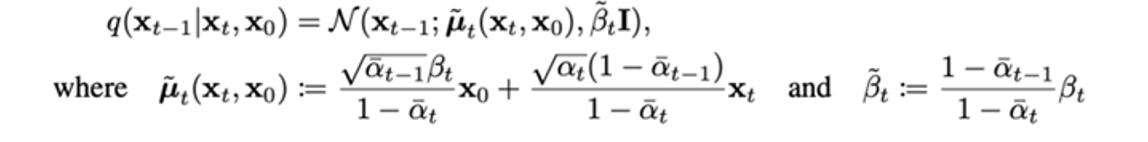
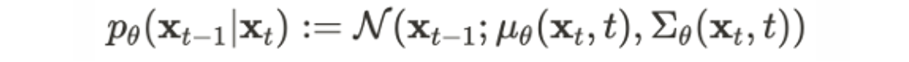
두 분포 모두 가우시안 분포를 따르기 때문에 둘 사이의 kl divergence는 좀 더 간략화해서 다음과 같이 나타낼 수 있다.

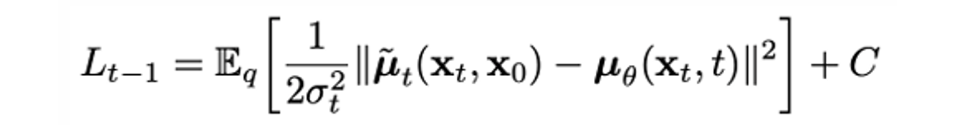
이때 $\mu_\theta, x_t$를 다음과 같이 파라미터화하면..

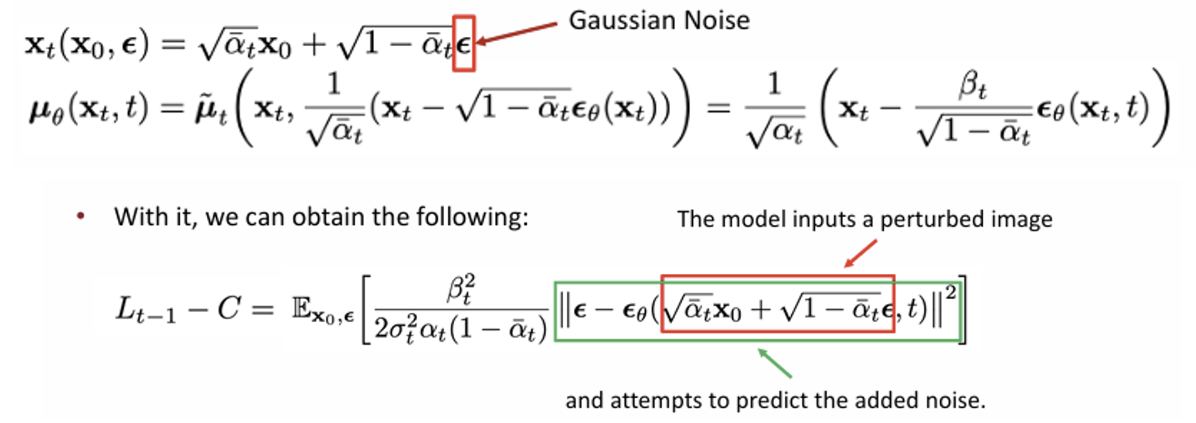
이 loss에서는 perturbed 이미지에 대해서 얼마만큼의 노이즈 가 추가되었는지를 계산하고자 한다.

3) $L_0$

DDPM에서는 연속 값을 비연속으로 바꾼다. 여기서는 이미지가 각 픽셀에 대해서 0~255의 값을 가진다는 것을 이용하여 생성하는 이미지의 픽셀 값 평균으로 loss를 구한다.

DDPM 논문 저자들은 1번과 3번 loss는 없애고 최종적으로는 간략화된 버전으로 2번째 loss를 최종 loss로 설정하였다.

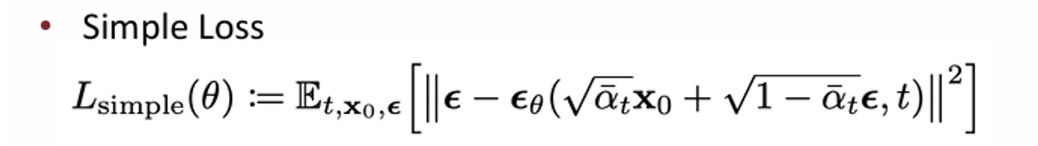
이때 t값이 작으면 loss를 작게, t값이 크면 loss를 키우는 식으로 weight를 줌으로써 t값이 클 때를 더 어려운 task로 정의하고 있다.

Pseudocode

x0, t, 엡실론을 위와 같이 정의한 다음에 위에서 구했던 최종 loss를 줄이는 방향으로 $\theta$를 학습

$x_T$는 standard gaussian dist에서 샘플링하였으며, neural network가 예측하는 평균을 사용하여 $x_{t-1}$ 로 가는 과정을 나타낸다.

이렇게 가장 베이스가 되면서 중요한 DDPM 논문을 정리해보았다. 다음 포스팅에서는 DDIM 등 더 advanced models에 대해 다뤄보도록 하겠다. 🙋‍♀️