그럼 이제 세 번째 생성형 모델인 GAN에 대해 정리해보자. GAN은 오래된 모델이긴 하지만 여전히 영향력 있는 모델인 것 같다. 그래서 이번에 학교에서 진행한 프로젝트도 GAN을 이용하기도 했었다. 그럼 이번 포스팅은 GAN의 베이직부터 시작해보도록 하겠다.

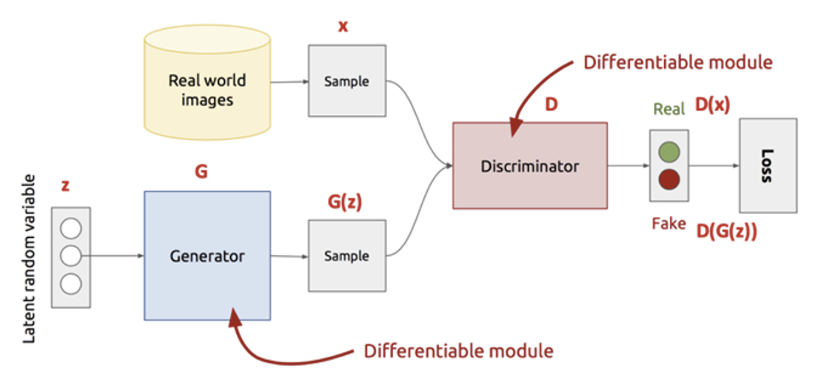
GAN의 파이프라인을 보면 Encoder와 Decoder 대신에 Discriminator 와 Generator 로 이름이 붙었다. GAN은 가짜 데이터와 진짜 데이터 사이에 대조적으로 학습하는 방식으로, 가짜 데이터를 생성하는 Generator와, 입력으로 가짜 및 진짜 데이터가 들어오면 어느 것이 진짜인지 분별하는 Discriminator가 있다. 그럼 GAN이 어떤 식으로 작동하는 아키텍처인지 천천히 알아보도록 하자.
Recap: Likelihood Training
파라미터 가 주어졌을 때 데이터의 확률을 likelihood라 하며, 이러한 likelihood를 가장 극대화하는 를 찾는 방식으로 학습하는 방식이다.
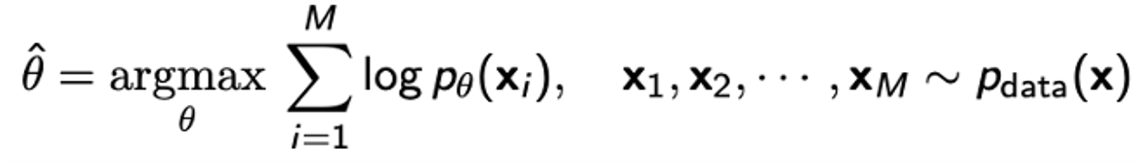
이는 결국 데이터 x가 분포 를 따를 때, 데이터 분포 와 생성 분포 사이의 KL divergence를 최소화는 방향으로 학습하는 것과 동일하다.
✨ Generative model의 공통점을 생각해보자.
생성형 모델에서 가장 큰 목적은 “그럴듯한” 데이터를 생성하는 것이다. 그러기 위해서는 실제 데이터와 닮아있는 데이터를 생성해야 한다.
- 이미지라면 realistic한 이미지를 생성해야 하고
- 텍스트라면 fluency, context등을 고려해 그럴 듯한 말들을 생성해야 한다.
따라서 생성된 데이터는 “실제 데이터 분포”와 닮아있어야 한다는 것이다.
Variational Autoencoder는 Reconstruction Error 를 이용해 input data와 decoder를 통해 생성된 output data 사이에 오차를 줄이는 방식으로 학습했다.
Normalizing flow는 explicit하게 likelihood를 극대화 하는 방식으로 학습했다.
따라서 GAN에서도 어떻게 실제 데이터 분포를 닮은 데이터를 생성하는 모델을 만들 것인지가 관건이 되는 것이다.
그런데 한 가지 의문점이 있다.
VAE나 Normalizing flow는 의 likelihood를 극대화하는 방향으로 학습을 진행했다. 그런데.. likelihood가 높다고 꼭 생성된 데이터의 퀄리티가 높다는 것일까?
물론 아주 optimal한 generative model이라면 likelihood가 높을 수록 더욱 실제 데이터같은 좋은 퀄리티의 데이터를 생성할 것이다. 하지만 완벽하지 않은 모델이라면 이야기가 달라진다. 꼭 likelihood가 높다고 해서 그게 생성 데이터의 퀄리티와 직접적으로 연관이 없을 수도 있다는 말이다.
GAN은 여기에서 likelihood의 필요성에 의문을 제기한다.
그리고 likelihood 없이 데이터를 생성하는 Likelihood-free model을 제안한다.
Generative Adversarial Networks (GANs)
GAN에서 정의하고 있는 problem task와 solution은 다음과 같다.
💡 Problem : 고차원의 매우 복잡한 데이터 분포에서 direct하게 샘플링을 하고 싶지만 그럴 수 있는 방법이 없다. (실제 데이터 분포는 알 수 없음)
✨ Solution : 그럼 복잡한 분포 말고 random noise와 같이 간단한 분포에서 sampling을 하자. 그리고 이 간단한 분포를 복잡한 데이터 분포로 변환시키자. 그럼 되는거 아냐?
🤔 Question : 그럼 이런 복잡한 변환을 어떻게 나타낼건데?
여기서 GAN의 답변은 바로 Neural Network이다.
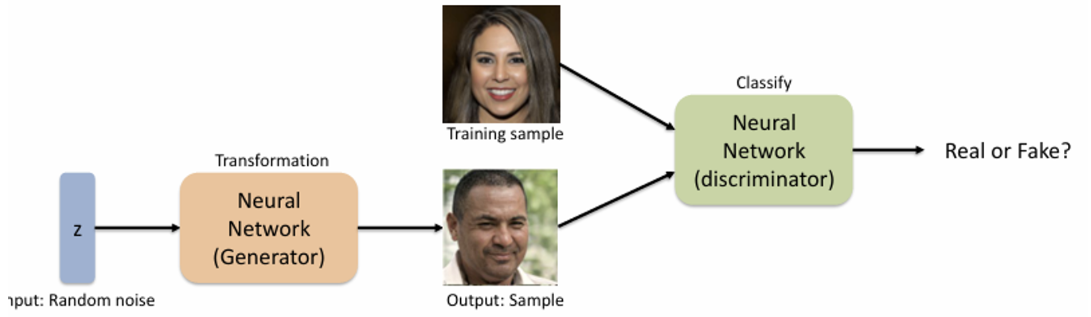
GAN은 총 두 가지 NN을 사용한다.
- Generator : Random noise(simple distribution)을 복잡한 고차원의 데이터 분포로 변환해주는 NN로, Discriminator를 속이기 위해 사실처럼 보이는 데이터를 생성한다.
- Discriminator : 실제 이미지와 Generator를 통해 생성된 이미지를 분별하는 NN이다.
Training GANs: Two-player game
GAN에서는 discriminator 와 generator 를 동시에 학습시켜야 하기 때문에 objective function은 다음과 같다.
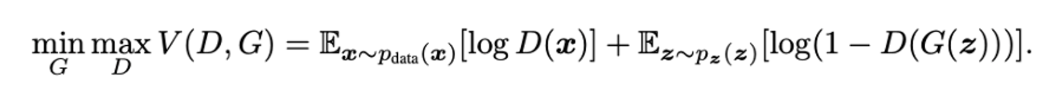
이 복잡한 수식을 하나씩 뜯어보자

- : 실제 데이터 x에 대한
Discriminator의 output - : random noise z에 대한
Generator의 output (생성 데이터) - : 가짜 데이터에 대한
Discriminator의 output
☑️ Discriminator의 목적: D(x)를 1에 가깝게, D(G(z))를 0에 가깝게 만들기
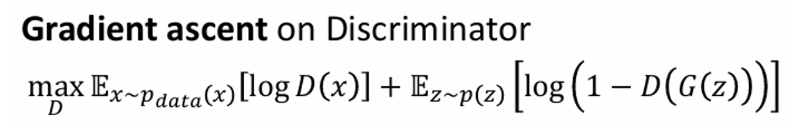
☑️ Generator의 목적: D(G(z))를 1에 가깝게 만들기

따라서 Discriminator와 Generator는 D(G(z)) 에 대해서 서로 반대 목적을 가지고 있다.
하지만 Generator의 입장에서 보면 학습이 잘 이뤄지지 않는다. 그 이유는 바로 loss 함수가 꼴로 이루어져 있기 때문에!
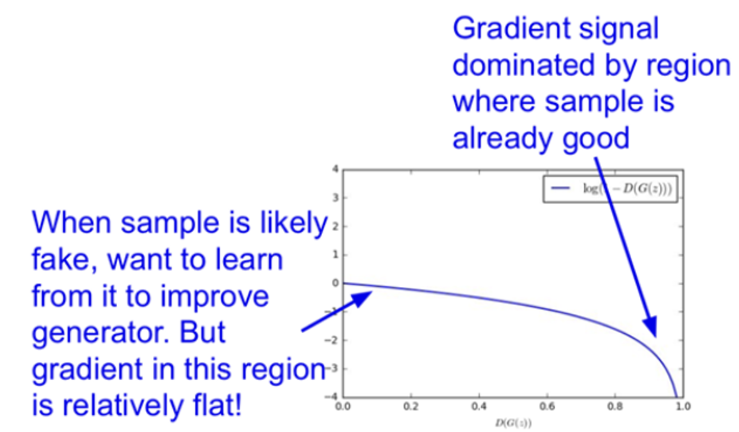
아래 x축이 D(G(z)), 즉 가짜 데이터에 대한 discrimiator의 output이다. D(G(z)) = 0이면 Generator는 더욱 사실같은 이미지를 생성하도록 학습해야 하며, D(G(z)) = 1이면 discriminator를 잘 속이고 있다고 판단할 수 있다.
하지만 loss 그래프의 기울기를 보면 그 반대이다.
D(G(z)) = 0 부근에서는 기울기가 flat 하기 때문에 파라미터 업데이트가 잘 일어나지 않고 학습이 어렵다. 반대로 D(G(z)) = 1 부근에서는 기울기가 steep 하기 때문에 이미 generator가 좋은 샘플을 만든다고 해도 계속해서 파라미터가 크게 업데이트 된다.
따라서 해당 loss 함수는 generator 입장에서는 안정적으로 학습할 수 없다.
🤔 그럼 반대로 생각해보자.
기존에는 discriminator가 옳을 likelihood를 최소화하는 것이었다. 그럼 반대로 discriminator가 틀릴 likelihood를 극대화하는 것으로 바꾸면 다음과 같이 목적 함수를 다시 쓸 수 있다.
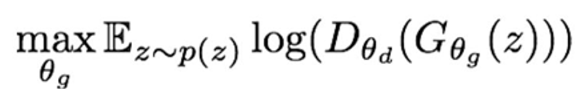
결국 discriminator 를 속인다는 점에서 기존의 목적 함수와 동일하지만 표현을 달리했을 뿐인데 좋은 성능을 보인다.
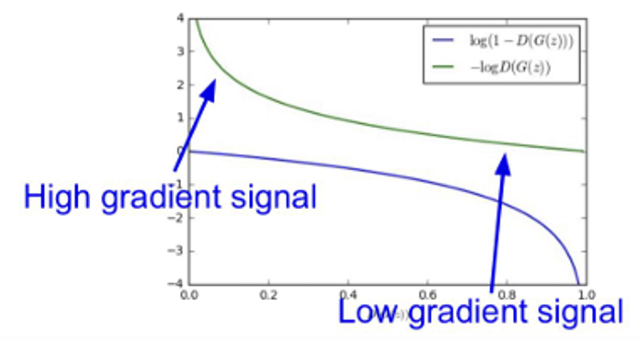
초록색이 새로운 목적 함수 그래프인데, D(G(z))=0인 부근에서 가파른 기울기를 가지며, D(G(z))=1 부근에서 완만한 기울기를 가진다. 따라서 실제로 GAN을 학습시킬 때에서는 이 방식으로 목적함수를 정의해서 사용한다.
Code snippets
for number of training iterations do
for k steps do
sample minibatch of m noise samples (z1,..., zm) from p_z
sample minibatch of m examples (x1,..., xm) from p_data
update discriminator (gradients ascending) # update for k times
end for
sample minibatch of m noise samples (z1,..., zm) from p_z
update generator (gradient ascending) # while update for 1 timecode snippet을 보면 학습이 1 iter 진행되는 동안 discriminator는 k step 업데이트 하지만 generator는 딱 한 번 업데이트 된다. 이때 두 업데이트 횟수에 차이가 있으므로 둘 사이의 조화를 잘 지켜야 한다.
discriminator가 너무 강하면 generator는 더 좋은 데이터를 생성하는데 실패할 것이며, generator가 너무 강하면 discriminator는 계속 틀리기만 할 것이므로 둘을 적절하게 학습시킬 수 있도록 하이퍼파하이터를 조정해야 한다.
이번에는 두 가지 GAN-based models를 간단하게 알아보자. 모델의 아키텍쳐를 바꾼 DCGAN과 도메인 사이를 넘나드는 CycleGAN이다.
DCGAN
: Deep Convolutional Generative Adversarial Networks
이번에는 단순히 두 NN을 이용해 학습하는 GAN을 deep conv로 쌓아보자. 이는 GAN에서 파생된 모델로 generator와 discriminator에 convolution이 사용되었다는 차이점이 있다.
DCGAN의 아키텍처는 다음과 같다.
- 모든 pooling layer → strided conv(discriminator), fractional-strided conv(generator)
- generator와 discriminator에 둘다 batchnorm 사용
- FC layer 삭제
- generator에서 모든 layer의 activation은 ReLU를, 마지막 output에서는 Tanh 사용
- discriminator에서 모든 layer의 activation은 LeakyReLU 사용
DCGAN에서 재밌는 실험 중 하나가 latent vector를 이용한 arithmetic!

CycleGAN
CycleGAN은 하나의 이미지에서 다른 도메인으로 translate하는 것을 말한다.

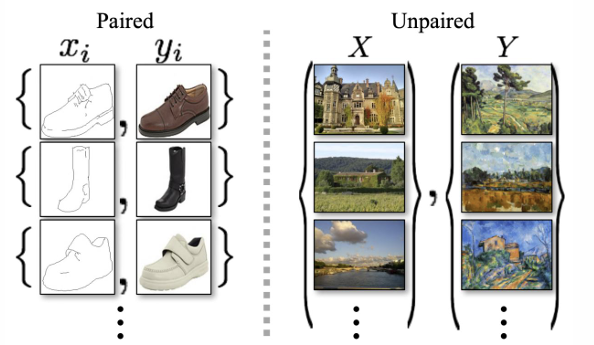
CycleGAN에서는 학습 데이터가 unpaired dataset을 사용한다.
여기서 unpaired dataset이란 다음 그림과 같이 1:1 쌍으로 묶여있는 데이터셋이 아니라 두 집합으로 되어있는 데이터셋을 말한다.
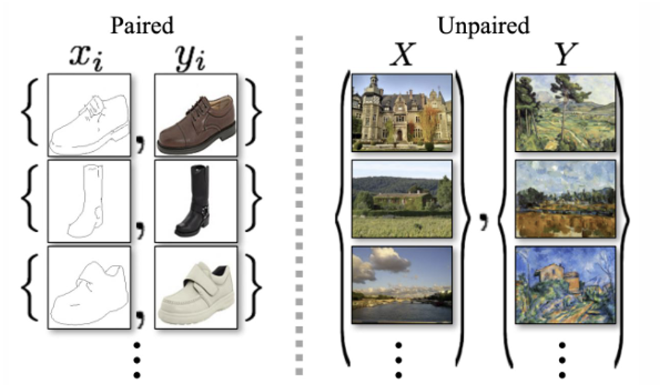
unpaired dataset의 경우 X와 Y라는 서로 다른 두 집합이 있지만 각각의 원소가 1:1 pair로 되어 있지는 않다.
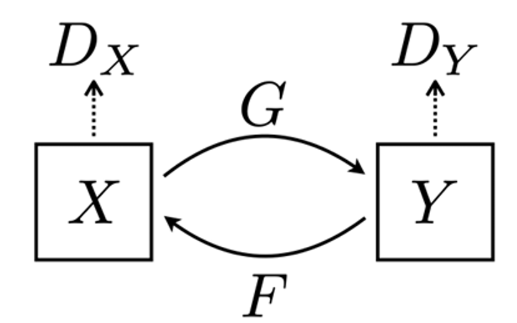
두 데이터 집합을 X와 Y라 하자.
기존의 GAN은 생성된 이미지(fake image)냐 실제 이미지(real image)냐를 구별하는 것이었다면 CycleGAN에서는 같은 집합의 이미지(in-domain image)냐 다른 집합의 이미지(out-domain image)냐를 구별해야 한다.
따라서 F와 G라는 transformation 함수가 있을 때 실제 같은 도메인에 속한 데이터인지, 혹은 다른 도메인에서 transform된 데이터인지 구별해야 한다.
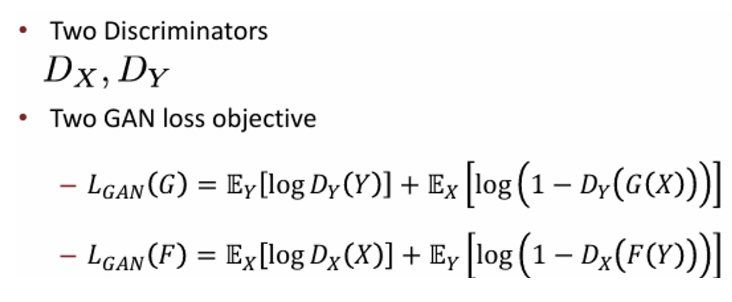
이에 추가로 transformation function F, G가 다른 도메인으로 더욱 잘 생성해내기 위해 Cycle consistency loss도 추가로 사용한다.
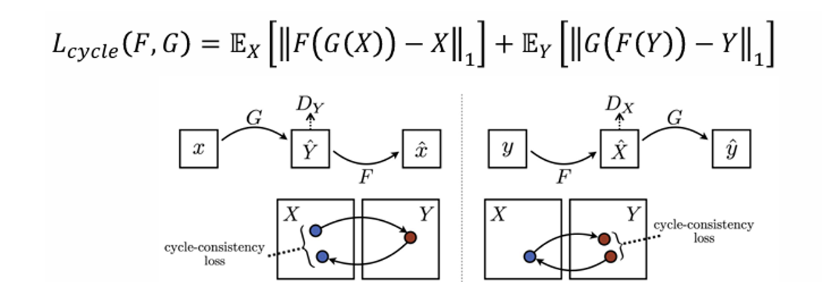
x → G(x)를 이용해 y를 생성했을 때, 이 생성된 y를 다시 F를 이용해 원래 도메인으로 매핑한다. 이때 처음 데이터 x와 F(G(x)) 사이의 loss를 구하는 방식이다.
Basics of GAN 포스팅은 여기서 마무리하고 이어서 Advanced GAN Models를 다음 포스팅에서 이어가도록 하겠다. 🙋♀️
