이전 포스팅에서 엔트로피가 무엇인지, 엔트로피를 증명하는 여러가지 이론들에 대해 소개했다. 그런데 여전히 의문이 든다. 엔트로피의 개념은 알겠는데… 그래서 어디에 쓰는건데? 🤔💭

이번 포스팅에서는 엔트로피가 데이터와 어떤 연관이 있는지 정리해보도록 하겠다.

Data Compression

엔트로피의 개념을 다시 recap해보자.

위키피디아에서 정의하고 있는 Entropy 는 다음과 같다.

🔥 The entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes.

엔트로피란 random variable의 가능한 결과값에 대한 “정보량”, “놀라운 정도”, 혹은 “불확실성”의 평균값이다. 예시를 보자.

로또의 번호를 생각해보자. 당첨되지 않을 숫자들에 대한 정보는 그닥 쓸모있지 않다. 왜냐, 당첨되지 않는 숫자들의 확률이 당첨될 숫자들의 확률보다 훨씬 높기 때문이다. 따라서 이런 정보는 “정보량이 낮다”, “놀라운 정도가 낮다”고 표현한다. 하지만 반대로 누군가 로또 당첨 숫자들을 알려주면 이거야 말로 엄청난 가치의 정보가 된다. 왜냐면 로또가 당첨될 확률이 현저하게 낮기 때문에.

따라서 엔트로피는 random variable의 결과값이 가지는 확률과 관련이 있다. 확률이 낮을 수록 엔트로피의 값은, 혹은 정보량이 많다. 그리고 정보량이 많을 수록 이러한 데이터는 저장하는데 많은 bits가 필요할 것이다.

자, 그럼 이를 토대로 데이터를 저장할 때 얼마나 많은 bits가 필요한지 수식으로 보자.

Raw bit content

random variable X의 raw bit content는 다음과 같다.

$|A_X|$는 r.v. X가 가질 수 있는 값들의 개수다. $H_0(X)$는 이러한 값들을 모두 표현하는데 필요한 bits 개수를 말한다.

예를 들어 $A_X = \{ a_1, a_2, a_3, a_4\}$이라고 하면 X가 가질 수 있는 값은 총 4개다. 그리고 이를 표현하는데 필요한 비트 수는 $\log _24 = 2$개이다.

raw bit content의 upper bound 는 반올림 값이 된다. 예를 들어 $|A_X|=5$라면 이를 표현하는데 필요한 bits는 $\log_25 = 2.xx$, 즉 반올림해서 3개가 된다.

x와 y의 pair가 주어졌을 때의 raw bit content는 각각의 raw bit content를 더한 것과 같다.

Raw bit content에서는 r.v.의 확률 값에는 관심이 없다. 그저 r.v.이 가질 수 있는 값들의 개수에만 초점을 맞춰 필요한 bits 개수를 계산할 뿐이다.

📌 이렇게 하면 문제점이 뭘까?

모든 데이터를 다 저장하다 보면 가장 큰 문제점은 메모리일 것이다. 정보가 넘쳐나는 이 세상에서 모든 자잘한 정보를 다 저장하라고? 사실상 불가능한 일이다. 따라서 우린 중요한 데이터만 압축해서 저장/전달해야 한다. 이때 “중요한” 데이터는 확률과 관련있다.

Lossy Compression

예를 들어서 보자. Ensemble X가 다음과 같이 정의되어 있다.

$H_0(X)$는 3이 될 것이다. 가능한 결과값이 8개 있으므로 이를 모두 표현하기 위해서는 3개의 비트가 필요하다. 그런데 잘 보면 확률값의 차이가 크다. a, b, c 의 경우 확률값이 높지만 e, f, g, h 는 확률값이 훨씬 낮다. 그럼 우린 굳이 이 모든 데이터를 저장할 필요 없이 확률값이 높은 것만 저장할 순 없을까?

1/16보다 낮은 확률을 가지는 데이터는 무시한다고 하면 저장해야 하는 값은 4개만 남는다. 그리고 이들을 저장하기 위해선 2 bits 만 필요로 하다. 이러한 방식을 lossy compression 이라 한다. 이는 데이터를 손실하는 문제가 있긴 하지만 필요한 bits의 양이 줄어든다.

Essential bit content

이번에는 꼭 필요한 데이터만 저장하는 essential bit content 이다. raw bit content 와 다르게 확률 값이 낮은 데이터는 버리고, 확률 값이 높은 데이터만 저장하는 방식이다.

우선 특정 확률 값 이상의 r.v. 결과값(x)을 추출한 집합을 $S_\delta$라 하자.

이때 $S_\delta$는 위 부등식을 만족하는 부분 집합 중 가장 작은 것을 의미한다. 예시를 보자.

Example

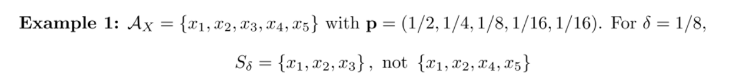
$\delta$=1/8일 때 $S_\delta$에 속한 확률 값의 합이 1-1/8 = 7/8을 만족하면 된다. 반대로 생각하면 제거할 확률의 합이 $\delta$면 된다.

사실 이러면 여러가지 경우의 수가 나올 수 있다. 따라서 $S_\delta$는 가장 작은 집합으로 정의되어 있으며, 위의 예시에서 $S_\delta = \{x_1, x_2, x_3 \}$이 된다.

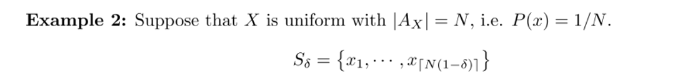
이번에 r.v. X는 uniform 하다. 이때는 모든 x에 대해 확률 값이 동일하기 때문에 가능한 $S_\delta$의 원소 개수는 $\ulcorner N(1-\delta )\urcorner$이 된다. 예를 들어 N = 8이면 모든 x의 확률 값은 1/8이 될 것이고, $S_\delta$는 7개가 된다.

그럼 이제 Essential bit content 를 계산해보자.

결국 raw bit content $H_0(X)$는 $\delta = 0$인 특별 케이스라 볼 수 있다.

위에서 봤던 uniform distribution 예시로 이번에는 essential bit content 를 구해보자.

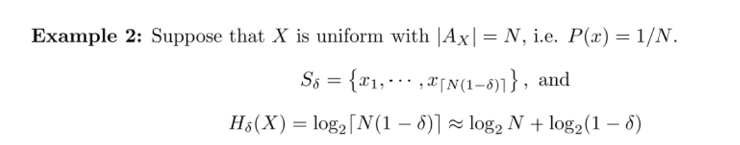
아까 구했던 $S_\delta$를 log에 그대로 넣어주면 된다. 어려울거 하나 없다. 그런데 여기서 한 가지 인사이트를 얻을 수 있다. 마지막 식에서 양변을 N으로 나눠준 후 N을 무한대로 보내보자.

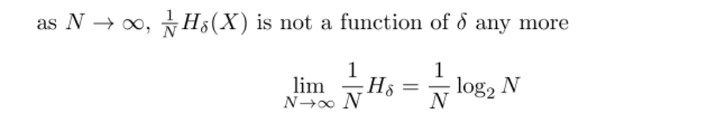
그럼 $\delta$가 들어간 항은 0으로 가서 없어지고, 결국 ${1\over N} \log _2 N$이 남게 된다.

Essential bit contents for blocks

이번에는 random variable X에서 N개의 i.i.d. random variables $X^N$ 튜플을 생각해보자. 이때 $X^N$은 N개의 x 시퀀스이다.

알파벳은 $A_X$의 곱, 확률은 각각의 x에 대한 확률 곱으로 나타낸다.

Raw bit content할 때 언급했던 additive Entropy를 이용하면 $H(X^N) = NH(X)$임을 알 수 있다.

예시를 보자.

Example

$X = \{ x, \{0,1 \}, \{ p, 1-p \} \}$로 정의되어 있다. 이때 $X^N$의 outcome은 $x = (x_1, x_2, ..., x_N)$이다.

이때 r(x) 를 x에서 1의 개수라고 정의하면 결국 x를 모두 더한 값이 된다. 여기서 $P_{X^N}$는 다음과 같다.

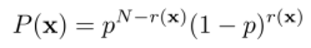
즉, 0일 확률이 p, 1일 확률이 (1-p)이므로 모든 x값에 대한 확률을 곱해주면 위와 같은 식이 성립한다.

여기까지 Data Compression에 대한 이론을 소개했다. 다음 포스팅에 이어서 shannon's coding theorem을 이어서 적어보도록 하겠다.