Intuition

A부터 Z까지가 하나의 사이클이고 그 다음은 AA, AB $\cdots$ 이므로 26진법으로 처리하면 되겠다고 생각했다.

Approach

어떤 문자 n이 들어오면 시작점인 'A'만큼 빼주고 +1을 해주면 우리가 원하는 대로 값이 변환된다. 문자도 결국엔 ASCII로 인코딩된 숫자이기 때문이다.

int converter(char c){
    return c-'A'+1;
}

예를 들어, BAC가 들어왔을 때 $26^2\times2+26^1\times1+26^0\times3$으로 계산을 해야한다. 즉, 문자열의 인덱스에 따라 지수를 조절해줘야한다. 이를 원활하게 하기 위해 문자열의 길이를 따로 구했다.

int len=0;
    for (int i=0;columnTitle[i]!=0;i++){
        len++;
    }

그리고 문자열의 인덱스가 증가할때마다 len변수를 1씩 감소시켜 지수를 1씩 줄였다.

int res=0;
    for (int i=0;columnTitle[i]!=0;i++){
        res+=converter(columnTitle[i])*power(--len);
    }

power함수는 거듭제곱을 반환하기 위해 만든 함수다. 26의 n제곱을 반환한다.

int power(int n){
    int res=1;
    for (int i=0;i<n;i++){
        res*=26;
    }
    return res;
}

Solution

int converter(char c){
    return c-'A'+1;
}

int power(int n){
    int res=1;
    for (int i=0;i<n;i++){
        res*=26;
    }
    return res;
}

int titleToNumber(char * columnTitle){
    int len=0;
    for (int i=0;columnTitle[i]!=0;i++){
        len++;
    }

    int res=0;
    for (int i=0;columnTitle[i]!=0;i++){
        res+=converter(columnTitle[i])*power(--len);
    }

    return res;
}

Complexity

• Time Complexity : columnTitle 배열을 하나씩 읽으면서 그때마다 거듭제곱을 계산해야 하기 때문에 $O(n^2)$이 소요된다.
• Space Complexity : columnTitle 배열을 담을 $O(n)$이 필요하다.

교수님 풀이

엄밀히 따지면 26진법은 아니다. Z가 26으로 대응되기 때문. 10진법이 10까지가 아니라 9까지인 것을 생각하면 된다.

이 문제에서 주목해야할 부분은 계산의 간소화이다. 예를 들어 아래와 같은 식을 계산해야 한다고 해보자.

내가 짠 알고리즘 대로라면 저 거듭제곱을 계산하기 위해 시간복잡도가 $O(n^2)$이 소모된다. 그러나, 지금부터 소개할 방법은 위와 같은 식을 $O(n)$에 계산할 수 있다.

식을 아래와 같이 26으로 묶어보자.

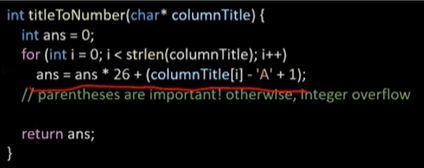
이제 규칙성이 좀 느껴질 것이다. 이전 계산 결과에 26을 곱하고 현재 문자값을 더해주는 작업을 반복하는 것이다. 아래는 각각 이를 적용한, 내가 쓴 코드와 교수님의 코드이다. 첫번째 항을 처리하는 방식이 조금 다르다.

int converter(char c){
    return c-'A'+1;
}

int titleToNumber(char * columnTitle){
    int len=0;
    for (int i=0;columnTitle[i]!=0;i++){
        len++;
    }

    int res=converter(columnTitle[0]);
    for (int i=1;columnTitle[i]!=0;i++){
        res=26*res+converter(columnTitle[i]);
    }

    return res;
}

Complexity

• Time Complexity : $O(n)$
• Space Complexity : $O(n)$

+) 더 나아가서, 거듭제곱 하나를 계산하는 방법에 대해서도 언급해주셨다.

질문 및 지적 환영합니다.