문제해결 자체 재수강
1.[LeetCode] 70. Climbing Stairs
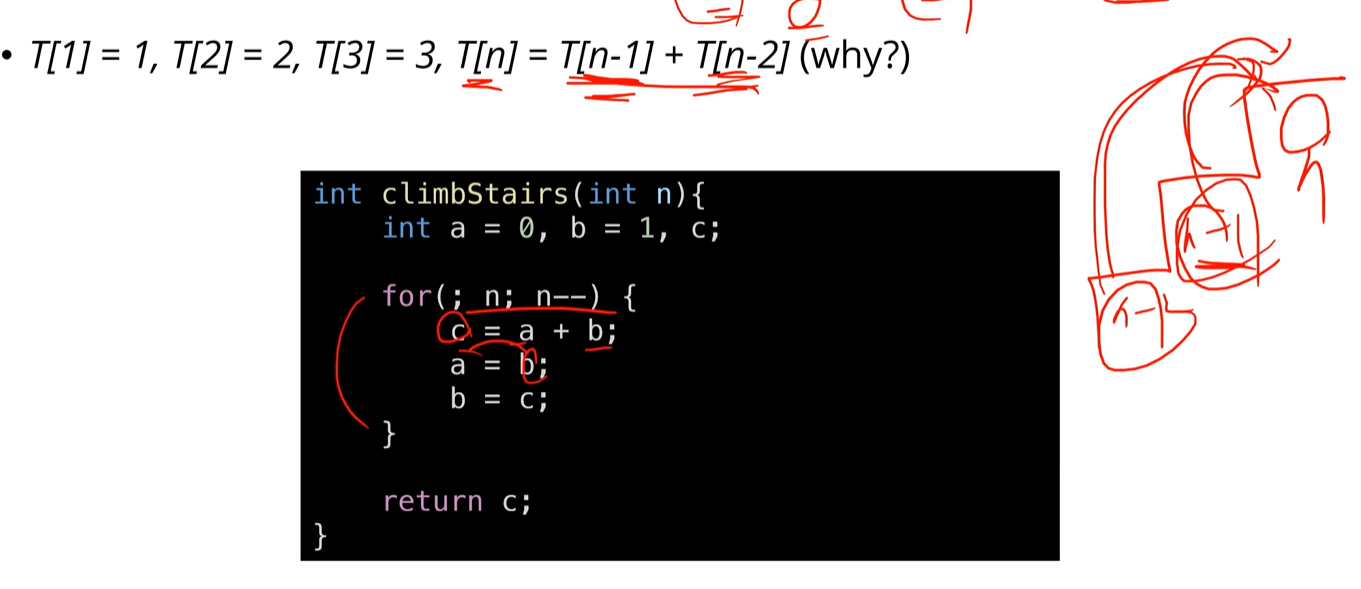
Intuition 문제는 간단했다. n을 1과 2로 이루어진 합으로 계산할 때 과연 몇가지 경우의수가 가능한가를 구하면 된다. Approach 1 처음에는 규칙을 찾아보니 $nC0+{n-1}C1+{n-2}C2+...$ 이런식의 규칙을 발견해서 이를 토대로 조합 함수를 만들고 다 더해보려했다. 그러나 이 코드는 factorial 과정에서 자료형 최대 범위...
2.[LeetCode] 172. Factorial Trailing Zeros
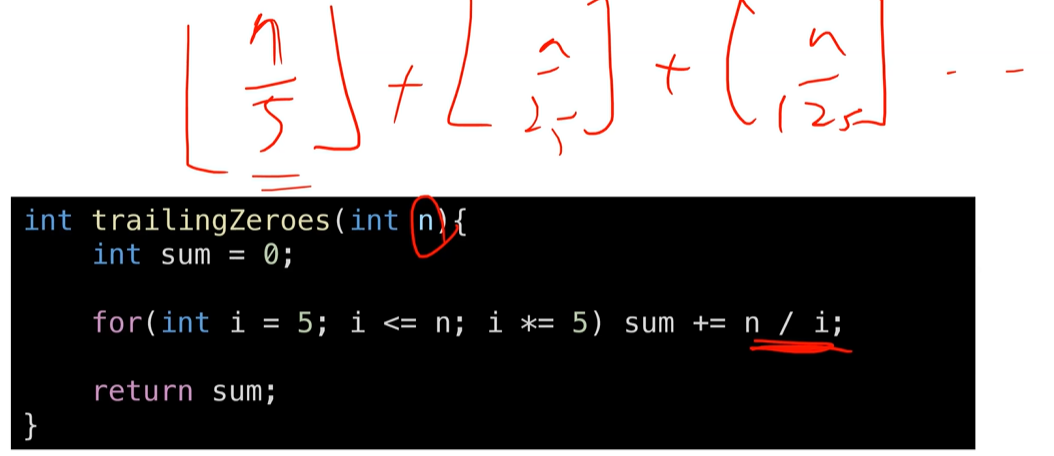
Intuition 팩토리얼의 계산결과 마지막에 붙는 0인 trailing zero가 몇개인지 세면된다. 기본적으로 0이 붙으면서 자릿수가 생기려면 10이 곱해져야한다. Approach && Solution 따라서 우리는 5의 배수에 집중하면 된다. 왜냐하면 2는 5보다
3.[LeetCode] 204. Count Primes, 그리고 에라토스테네스의 체 시간복잡도 증명
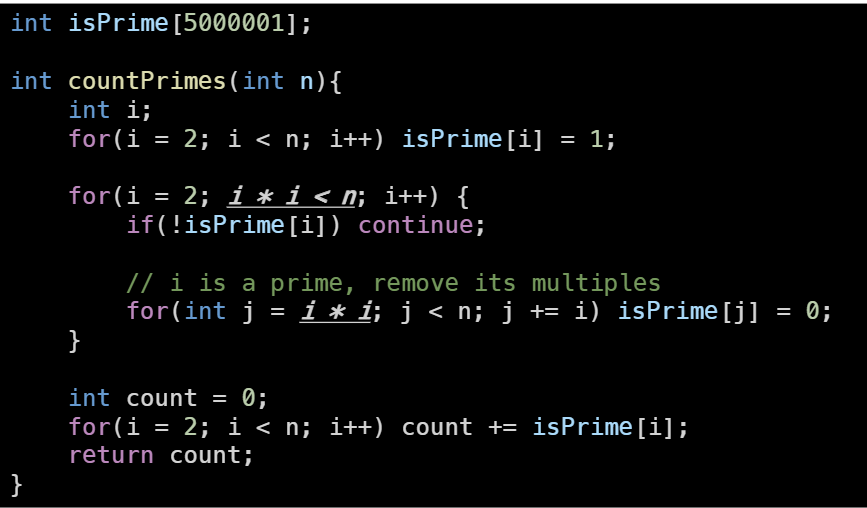
Intuition 문제를 보자마자 에라토스테네스의 체가 떠올랐다. 숫자 하나의 소수 여부를 판별하은 제곱근까지 나누어서 나누어 떨어지지 않는다면 소수라고 판단할 수 있다. 그러나 여러개의 소수를 대량으로 판별하는 데에는 에라토스테네스의 체가 훨씬 효과적이다. 문제를 풀
4.[LeetCode] 283. Move Zeroes

Intuition 순서를 유지하면서 0만 뒤로 보내면 되는 것이니, 앞에서 부터 순차적으로 읽으면서 0이 아닌 숫자를 앞으로 가져오면 되겠다고 생각했다. Approach >앞에서부터 읽어가면서 0이 아닌 숫자를 0과 바꾸면서 순서는 유지시키기 위해, 이동할 위치(0을 가리키는)의 인덱스와 0이 아닌 숫자의 인덱스 각각을 가리키는 변수를 만들었다. >**m...
5.[LeetCode] 136. Single Number

Intuition 숫자 개수만큼 배열을 만들어 놓고 해당 숫자가 등장할때마다 배열을 +1하면 어떤 것이 1개 나왔는지 알 수 있을 것이라고 생각했다. Approach >문제가 constant extra space로 제한을 두고 있으므로 숫자의 범위가 중요해졌다. 다행히 숫자가 $-3 * 104 \leq nums[i] \leq 3 * 104$로 그리 많지는 ...
6.[LeetCode] 53. Maximum Subarray

Intuition 1 && Approach 1 subarray 형태를 찾아야하니 누적합을 활용하면 좋을 것 같다는 생각이 들었다. 누적합 배열을 만들면 $an$부터 $a{n+k}$까지의 합은 $pre{n+k}-pre{n-1}$으로 $O(1)$에 구할 수 있다. 예를 들어, 아래와 같은 배열이 있을 때 $$[5,9,-1,-3,2] $$ 누적합은 아래와 같...
7.[LeetCode] 169. Majority Element

Intuition 배열의 길이가 50000개로 제한되어있기 때문에 지금까지 배열에 등장한 숫자를 저장해서 그게 몇 개 나왔는지 체크하는 것이 가능할 것이라고 생각했다. Approach > 어떤 숫자가 몇개 나왔는지 저장하기 위해서 구조체를 만들었다. num은 배열의 첫번째 원소로(문제의 숫자 범위가 광범위해서), 수량은 0으로 초기화를 시켰다. > 배열을...
8.[LeetCode] 13. Roman to Integer

Intuition 로마 숫자 종류가 7개로 한정되어 있고, 기본 규칙은 무조건 큰 숫자에서 작은 숫자의 흐름인데, 그것에 반할 때에만 특수하게 처리하므로 숫자 7개를 따로 dictionary처럼 사용하면서 문제를 풀면 되겠다고 생각했다. Approach > 우선 숫자 7개를 dictionary처럼 쓸 수 있도록 함수를 만들어줬다. > 일반적인 경우에는 그...
9.[LeetCode] 171. Excel Sheet Column Number
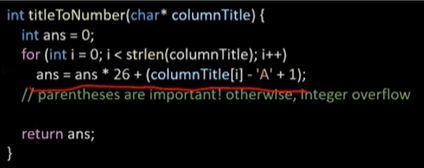
Intuition A부터 Z까지가 하나의 사이클이고 그 다음은 AA, AB $\cdots$ 이므로 26진법으로 처리하면 되겠다고 생각했다. Approach > 어떤 문자 n이 들어오면 시작점인 'A'만큼 빼주고 +1을 해주면 우리가 원하는 대로 값이 변환된다. 문자도
10.[LeetCode] 3. Longest Substring Without Repeating Characters

Intuition 반복을 피하기 위해서는 이전에 해당 문자가 나왔는지를 알아야한다. 마침, 등장할 수 있는 문자는 ASCII Table에 있는 128개가 전부이니 등장여부를 체크하는 배열을 만들 수 있다. 문자열을 돌다가 중복된 문자라면, 해당 문자가 나왔던 위치의 다
11.[LeetCode] 134. Gas Station
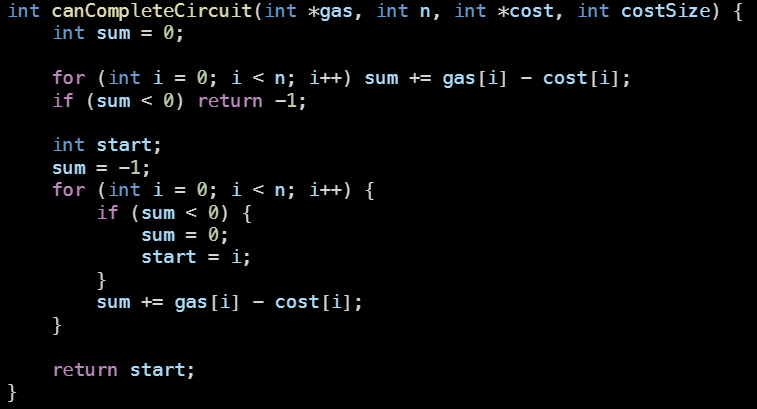
Intuition 일단, gas[i]보다 cost[i]가 크다면 시작자체가 불가능하므로 그 지점은 답이 될 수 없다. 마찬가지로 $i^{th}$ station에서 $(i+1)^{th}$ station으로 이동할때에도 gas[i]만큼 채우고 cost[i]만큼 소모하므로,
12.[LeetCode] 402. Remove K digits

Intuition 자릿수를 중요하게 생각해야 한다. 더 큰 자릿수에 있는 수는 더 큰 영향력을 갖는다. 따라서 rough하게 생각했을 때 자릿수가 클 수록 작은 수를 가져야한다고 예상해볼 수 있다. 조금 더 구체화하면 숫자 $abcd\cdots$가 $a\leq b\le
13.[LeetCode] 350. Intersection of Two Arrays II

Intuition 두 배열을 각각 살펴보고 공통되는 것을 결과배열에 담아주면 되겠다고 생각했다. Approach >두 배열을 순회하며 등장할 수 있는 숫자 0~1000을 count하는 배열 n1, n2를 만들었다. 이때, 원소 i의 개수는 n[i]에 저장된다. res는
14.[LeetCode] 2. Add Two Numbers

Intuition 더하기를 진행할 때 일의 자리부터 진행하게 되는데, 문제에서도 역순으로 된 linked list를 input으로 주고 있기 때문에 주어진 linked list를 순서대로 순회하며 더하면 될 것이라 생각했다. 이때, carry와 남는 자리수들에 대해서
15.[LeetCode] 23. Merge K Sorted Lists

Intuition 이미 정렬되어 있는 배열을 합쳐서 다시 정렬시킨다는 상황자체가 Merge Sort의 후반부 과정과 유사한 상황이다. 그러나 코드를 조금 더 직관적으로 작성하기 위해 두 개씩 배열을 비교하는 병합 정렬과 달리, 한번에 모든 배열을 비교하는 방식을 채택하
16.[LeetCode] 19. Remove Nth Node From End of List

Intuition 최대로 나올 수 있는 Number of Nodes가 30개이기 때문에 연결 리스트를 순회하면서 각각의 Node를 포인터 배열에 저장해놓는다면, 원하는 위치의 Node를 지우는 작업은 $O(1)$에 수행할 수 있을 것이라 생각했다. Approach >연
17.Detecting the First Element in the Loop + Bonus Problem
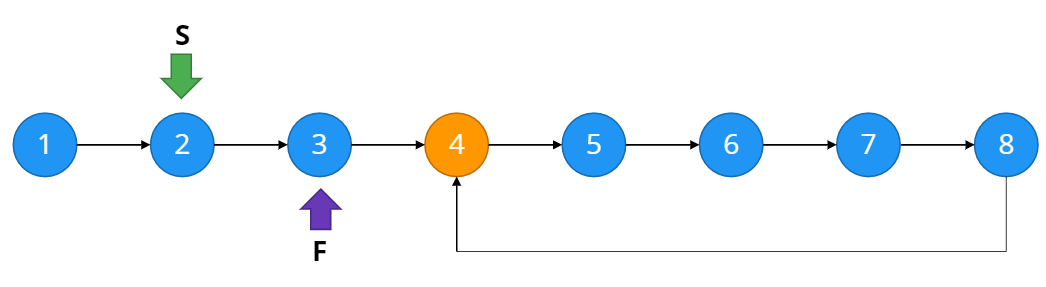
Detecting the First Element in the Loop Description 위 그림과 같이 Single Linked List에서 한 개 이하의 loop가 존재한다고 가정했을 때, 그 loop가 시작하는 위치를 찾는 문제이다. 단, loop의 마지막은 마지막 index이다. Naïve Approach 연결 리스트 일순 과정에서 각각의 no...
18.[LeetCode] 845. Longest Mountain in Array

Intuition 값이 올라가기 시작하는 지점부터 내려오는 지점까지의 길이의 최댓값을 구하는 문제이다. Literally 산을 찾으면 된다. 그러기 위해선 올라가는 부분과 내려가는 부분, 그리고 하산이 끝나는 지점을 특정시켜줄 수 있어야 한다. Approach 올라가
19.[LeetCode] 1793. Maximum Score of a Good Subarray

Intuition 이 문제를 한 줄로 요약하면 (길이)*(최솟값)을 최대로 만드는 것이다. 길이를 확정시킨다음 최솟값을 결정할 수도 있고, 최솟값을 결정한 다음 길이를 최대화시킬 수도 있다. 나는 전자의 경우 $O(N)$, 후자의 경우 그보다는 효율적일 것이라고 판단해
20.[LeetCode] 1712. Ways to Split Array Into Three Subarrays
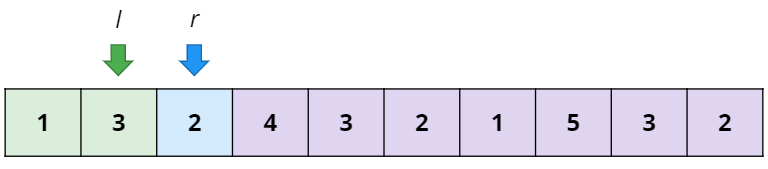
Intuition left, mid, right의 범위를 지정해주는 것이 우선적으로 필요하다. 한번에 지정하기는 힘들기 때문에, left를 먼저 지정하고 나머지 mid와 right를 지정하는 느낌으로 생각했다. Approach >본격적으로 시작하기에 앞서, 그때그때
21.[LeetCode] 1444. Number of Ways of Cutting a Pizza
Intuition 문제를 좀 더 간단하게 생각해보면, k-1번 나눠서 그때마다 사과가 최소 1개 이상 있도록 만들어주는 문제이다. 그러기 위해 매번 선을 나눌때마다, 위아래 또는 양옆에 모두 사과가 있는 유효한 선인지를 검증하며 모든 경우의 수를 카운트하는 방식을 택했
22.[LeetCode] 713. Subarray Product Less Than K
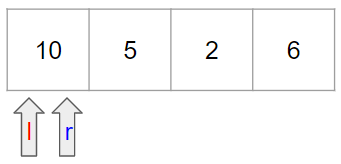
Intuition contiguous한 subarray를 찾아야 하는 점에서 two pointer의 느낌을 받을 수 있었다. subarray의 양 끝을 조절하며 k와 곱을 비교해가면 문제를 풀 수 있을 것이라 생각했다. Approach subarray의 양 끝을 two
23.[LeetCode] 1823. Find the Winner of the Circular Game

문제의 구조 자체가 Circular Linked List와 매우 유사하다. Node를 하나씩 순회하며 처음과 끝이 연결된 구조이고, Node를 삭제할 수 있다. 매 턴마다 K번씩 순회를 하는 과정을 N개만큼 반복한다. $O(KN)$Node 개수만큼의 공간이 필요하다.
24.[LeetCode] 11. Container With Most Water
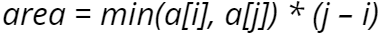
Intuition 투포인터 문제인 느낌을 잡게되고 Narrowing down 방식으로 접근하게 되면, 아래의 area를 최댓값으로 만드는 경우를 찾는 것이라는 것을 쉽게 알 수 있다. 다른 걸 불필요하게 볼 필요 없다. 뒤의 j-i는 1씩 동일하게 감소하므로 사실상 상수 취급한다. 신경써야할 부분은 min의 값이 변경되는 것인데, min의 값이 변경되려면...
25.The Tower of Hanoi problem
Description 하노이 탑 문제는 재귀로 풀이할 수 있는 대표적인 문제이다. 하노이 탑 문제를 탑 다운 방식으로 쪼개보면, >1. A막대의 가장 밑에 있는 disk를 제외한 나머지 disk들이 B막대에 위치하고 (일련의 과정들에 의해) >2. A막대의 가장 밑에 있는 disk가 C막대로 이동하고 >3. B막대의 n-1개의 disk들을 C로 이동시...
26.[LeetCode] 1545. Find Kth Bit in Nth Binary String

Intuition n의 최댓값이 20이기 때문에, $S_{20}$까지의 모든 문자열을 만들어 확인해보는 것이 가능하지만, 문제의 description에서 base case와 점화식이 주어지므로 재귀를 고려해볼 수 있다. Approach $Sn$문자열은 1이 위치한 $
27.[LeetCode] 486. Predict the Winner

Intuition optimally하게 play하는 것이 이 문제에서 가장 관건이었다. 처음에는 greedy하게 시도했으나, optimal한 플레이를 할 수 없었다. 이를 재귀를 통해 모든 경우의 수를 끝까지 살펴보고 leaf node에서 top으로 올라오는 과정에서
28.[LeetCode] 1863. Sum of All Subset XOR Totals
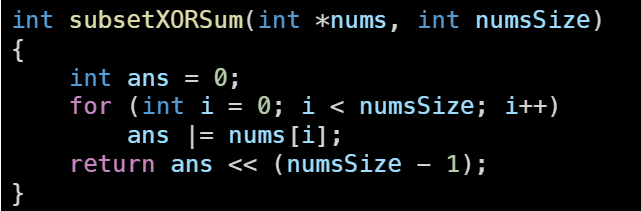
Intuition 모든 subset의 xor을 체크해야하기 때문에 문제의 description에서 부터 모든 경우의 수를 확인해야 함을 알 수 있다. 이를 위해 재귀를 고려해보았다. Approach 각 원소는 있거나(1), 없거나(0) 둘 중에 하나의 경우이다. 앞
29.[LeetCode] 60. Permutation Sequence

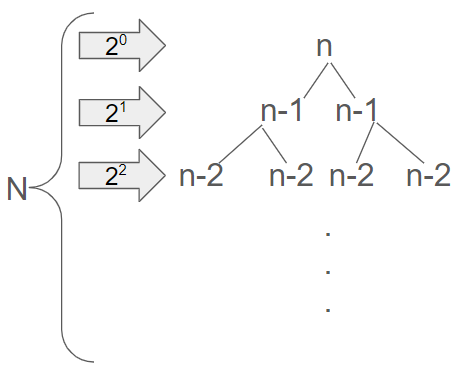
Intuition 만들 수 있는 문자열의 경우의 수를 보는 문제인데, 중복이 안되는 것이다. Approach & Solution 중복 여부를 알기위해 mask 배열을 사용했다. Complexity Time Compelxity recursion의 과정을 tree구조로 표현했을 때, 첫번째 깊이에서 n 두번째에서 n-1개씩 n개 세번째 n-2개씩 n(n-1)...
30.[LeetCode] 77. Combinations
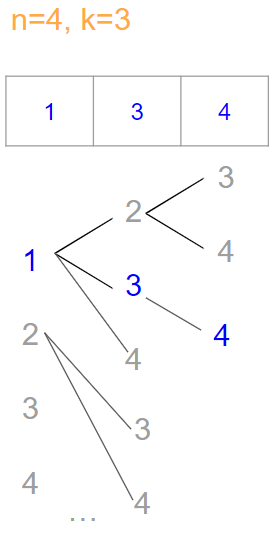
Intuition 모든 조합의 경우의 수를 확인하기 위해 재귀로 접근한다. Approach 본격적으로 시작하기에 앞서 leetcode에서 2차원 배열을 반환받는 방식이 조금 특이하기에 이것부터 짚고 넘어가야한다. skeleton code에 int* returnSize와
31.[LeetCode] 494. Target Sum
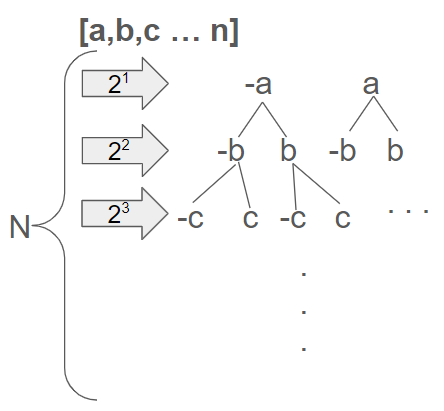
Intuition 배열을 순회하며 각 원소마다 +인 경우와 -인 경우를 모두 확인한다. Approach&Solution Time Complexity $\therefore O(2^n)$ 지적 및 질문 환영
32.[LeetCode] 733. Flood Fill

Intuition 4-directionally라는 문제 조건에 맞춰, 재귀함수를 상하좌우로 호출하면 될 것이라고 생각했다. Approach >본격적으로 문제를 풀기에 앞서 2차원 배열을 반환하기 위한 세팅을 해줘야한다. 관련 설명은 [LeetCode] 77. Combinations에 기술했다. >특정 좌표에 문제에서 원하는 color로 색칠을 해주는 함수...
33. [LeetCode] 52. N-Queens II
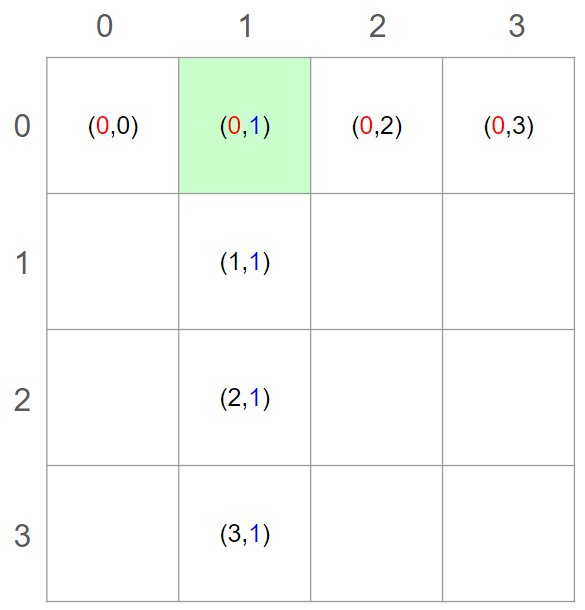
Intuition 퀸이 공격할 수 있는 가로,세로, 대각선 방향을 체크하면 되겠다고 생각했다. Approach 퀸을 배치할 때마다, 이전에 놓인 퀸 중 가로, 세로, 대각선 방향으로 공격할 수 있는 퀸이 존재하는지 확인해야 한다. >이를 위해 이 체스판 좌표의 특징(
34.[LeetCode] 44. Wildcard Matching
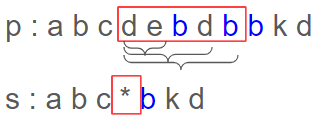
Intuition '*'가 등장할 때마다 이를 분기로 삼고 재귀를 호출하는 방식으로 진행하면 되겠다고 생각했다. 그리고 이렇게 가능성 있는 케이스를 모두 살펴보고 한번이라도 가능한 케이스가 발견되면 true를 반환하면 될 것이라고 생각했다. Approach >문자열 s와p 둘 중 하나라도 끝날때까지 문자열을 순회한다. 이때, 두 문자가 같지 않은 경우는 따...
35.[LeetCode] 1079. Letter Tile Possibilities

Intuition 같은 문자끼리는 구분하지 않으므로 개수를 기준으로 풀이하면 될 것이라 생각했다. Approach&Solution 교수님 풀이 예를 들어, 우리가 모든 문자를 다 써야하는 문제라면 단순히 팩토리얼 계산으로도 쉽게 해결할 수 있다. (특히, 이 문제의
36.[LeetCode] 1011. Capacity To Ship Packages Within D Days

Intuition 가능한 capacity를 이진탐색을 통해 후보를 정한 다음, 그때그때 그것이 가능한지 체크한다. 이때, 점점 capacity가 작아지도록 이진탐색하여 최솟값을 찾는다. Approach >어떤 시점 x부터는 capacity가 모두 가능해진다. 이 x를 찾기 위해 이진탐색을 진행할 것이다. 위의 표에서는 편의를 위해 최댓값을 $2^{31}$...
37.[LeetCode] 400. Nth Digit
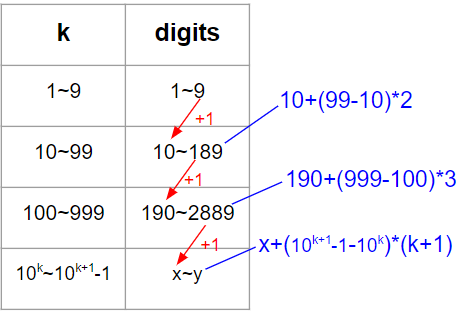
Intuition 이진탐색으로 output후보를 탐색하면서, 그때그때마다 해당 후보가 정답범위에 있는지를 체크하기로 했다. Approach 예를 들어 12는 10에서 2만큼 차이가 나고, 또 두자리수이기 때문에 10에서 1씩 커질때마다 digits는 2씩 증가한다. 따
38.[LeetCode] 275. H-Index II

Intuition citations.length에 따라 h의 최댓값이 결정되는 점에 주목하여 이진탐색을 진행했다. Approach [3,3,100] 이라는 배열이 있을 때, 배열의 길이가 3이므로 h는 최소1, 최소3 의 범위 내에서 구할 수 있다. 1부터 3까지의
39.[LeetCode] 33. Search in Rotated Sorted Array

Intuition 문제에서 한번 회전된 배열이 input으로 들어오는 경우, 이진탐색을 적용할 수 없다. 즉, 회전되기 전의 배열을 구해야한다. Approach 회전되기 이전의 배열을 구하기 위해 회전이 된 기준점인 pivot을 이진탐색을 통해 탐색했다. >우선, numsSize가 1인 경우의 pivot은 0일수밖에 없고, 회전이 되어있지 않은 케이스는 ...
40.[LeetCode] 4. Median of Two Sorted Arrays
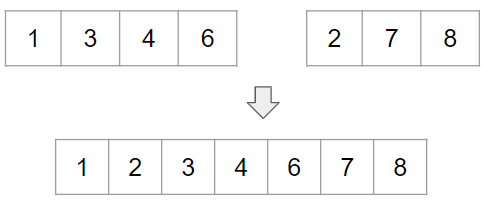
Intuition $O(log(m+n))$의 시간 복잡도 내에 문제를 해결해야 하기 때문에, 실제로 두 배열을 합치는 방식은 배제한다. 실제로 정렬을 수행하지 않으면서 median을 찾는 방법을 고안해야한다. 중앙값이 $N$개의 원소들을 정렬했을 때 $N\over2$
41.[LeetCode] 856. Score of Parentheses
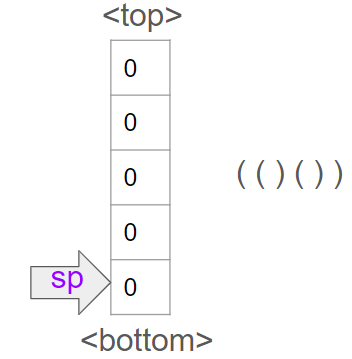
Intuition stack 에 여는괄호 '(' 를 넣으면서 닫는괄호 ')' 가 나올 때마다 경우에 맞게 처리해주는 방식으로 풀이했다. Approach '(()())' 을 예시로 설명해보겠다. 그림으로 표현해보면 아래와 같은 상황이다. sp는 스택포인터다. 여는 괄호
42.[LeetCode] 946. Validate Stack Sequences

pushed의 원소들을 stack에 push하면서 popped의 원소들과 비교해본다.예시를 들어보겠다. sp는 stack pointer, pushp와 popp는 각각 push pointer, pop pointer다.1,2,3은 popp의 4와 일치하지 않으므로 모두 s
43. [LeetCode] 462. Minimum Moves to Equal Array Elements II
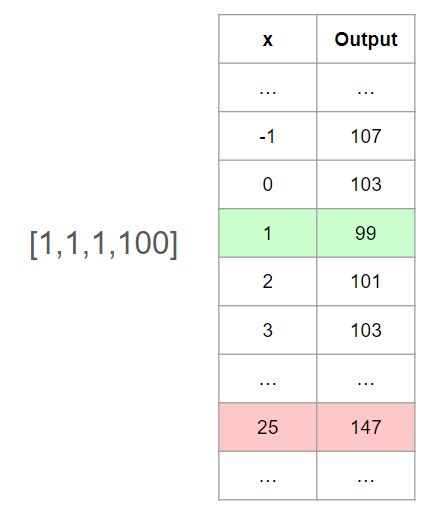
Intuition $argminx\sum\left\vert arri-x \right\vert$을 찾는 문제로 귀결된다. 이때 $x$는 중간의 적당한 어떤 값인 평균이나 중앙값 중 하나일 것이라고 추측했다. Approach 중앙값일 때 결과값이 최소화되고 중앙값에서 멀어
44.[LeetCode] 279. Perfect Squares
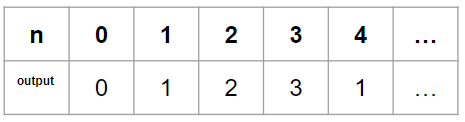
제곱수들만의 합으로 특정 숫자를 구성한다. 이때, 최소한의 숫자가 몇개인지 구하는 문제이다.LIS의 변형 느낌이다.이번 문제는 쉽기때문에 간단하게 요약 작성하였다1을 만들기 위해서는 1만 있으면 된다.2는 1+1, 0+2 모두 가능하지만, 문제 조건상 전자만 가능하다.
45.[LeetCode] 416. Partition Equal Subset Sum

Intuition 각 원소들의 사용여부에 대해 모든 경우의 수를 따져본다. Approach [1,5,11,5] 의 배열을 예시로 들겠다. 전체합의 반인 11을 만들 수 있는지 확인해야한다. 첫번째 원소 1의 경우 사용하지 않게 되면 0을 만들 수 있고, 사용하면 1을
46.[LeetCode] 516. Longest Palindromic Subsequence
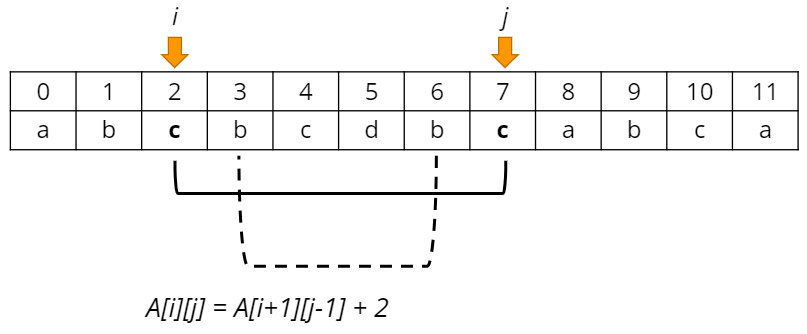
Intuition 임의의 두 문자가 같거나 다른지에 따라 관계식에 변화가 있을 것이라고 추정했다. Approach >Ai : [i:j]의 범위에서 Longest Palindromic Subsequence(이하 LPS) 위와 같이 문제를 정의한다. 길이가 1인경우에는
47.[LeetCode] 1143. Longest Common Subsequence

Intuiton longest와 subsequence의 키워드로 DP풀이를 고려해볼 수 있다. text1과 text2의 문자를 하나씩 비교하며 같을 때마다 Longest Common Subsequence(이하 LCS)의 길이가 +1될 것이라고 예상했다. Approach
48.[LeetCode] 72. Edit Distance

Intuition 작은 문자열부터 원래문자열까지 하나씩 늘려가며 문제를 해결할 수 있을 것이라 예측했다. Approach 문제 재해석 >Def.) arri:=word1[:i]가 $word2[:j]로 convert 되는데 필요한 최소 cost 위와 같이 부분 문제를 정
49.[LeetCode] 312. Burst Balloons
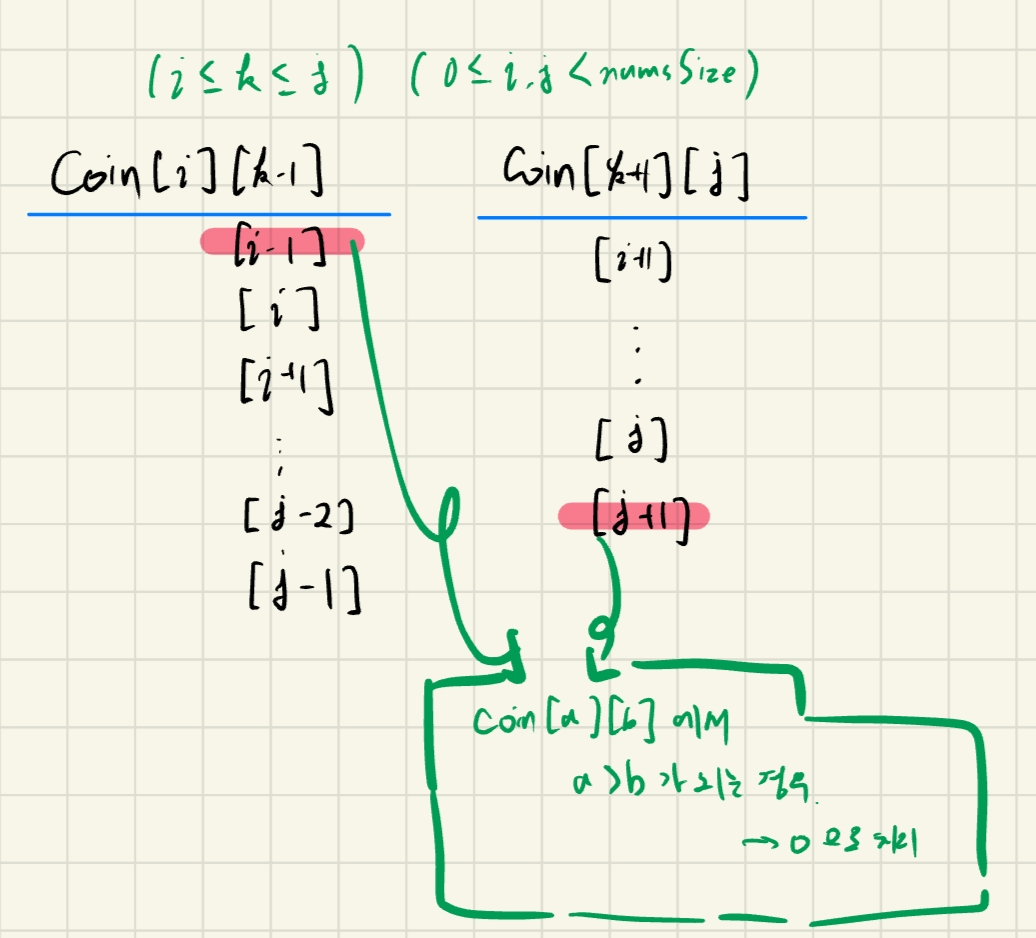
Intuition 하나씩 풍선을 터뜨려가면서 그때그때 최선의 선택을 찾는 알고리즘은 불가능해보였다. 작은 케이스의 결과가 큰 케이스의 결과를 알아내는 데에 도움을 줄 수 있어보였다. Approach >Def.) numsi:j]에서 최대로 구할 수 있는 코인의 수를 co