Intuition

같은 문자끼리는 구분하지 않으므로 개수를 기준으로 풀이하면 될 것이라 생각했다.

Approach&Solution

int alphabet[26]; // A-Z까지 각각 몇 번이 나오는지 카운트하는 배열
int cnt; // 결과값

void counter(){
    for (int i=0;i<26;i++){
        if (alphabet[i]>0){ // 1 이상이면 해당 문자를 다 쓰지 않았다는 뜻, 또한 이 line이 사실상 base case가 됨
            alphabet[i]--; 
            cnt++; // 모든 문자를 다 썼을때만 결과값을 카운트하는게 아님
            counter();
            alphabet[i]++;
        }
    }
}

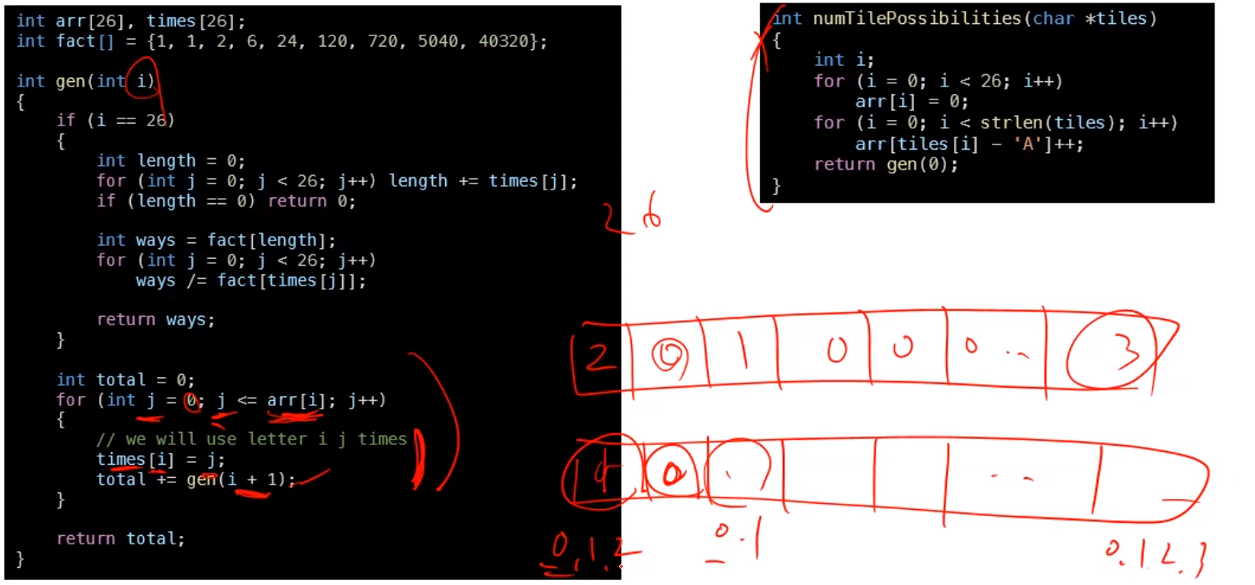
int numTilePossibilities(char* tiles) {
    for (int i=0;i<26;i++) alphabet[i]=0;
    cnt=0;

    for (int i=0;tiles[i]!=0;i++){
        alphabet[tiles[i]-'A']++;
    } 

    counter();
    return cnt;
}

교수님 풀이

예를 들어, 우리가 모든 문자를 다 써야하는 문제라면 단순히 팩토리얼 계산으로도 쉽게 해결할 수 있다. (특히, 이 문제의 경우 n이 작으므로)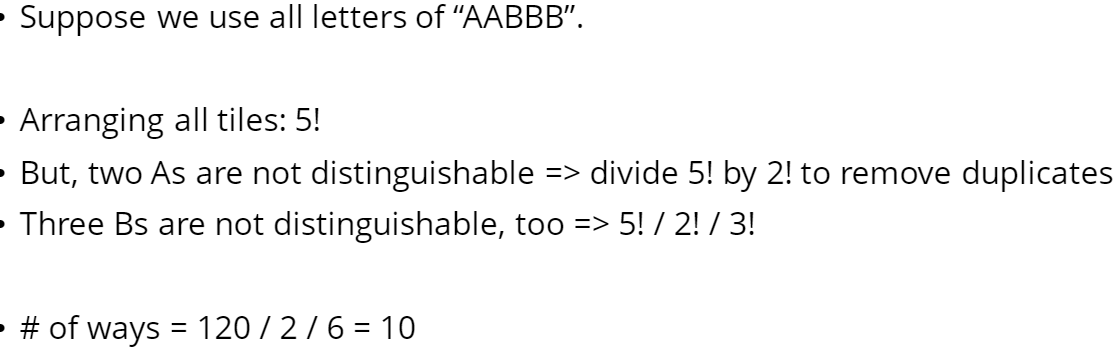

그러나 이 문제는 문자를 다 사용하지 않는 경우에 대해서도 고려해야하므로, 이 과정을 재귀로 풀이해볼 수 있다.
예를 들어 문자 AACZZZ가 있다면,
A 1개, C 0개, Z 0개 일 때의 경우의 수 부터
A 1개, C 1개, Z 0개
A 1개, C 1개, Z 1개
A 1개, C 1개, Z 2개
.
.
.
A 2개, C 1개, Z 3개 일 때의 경우의 수에 이르기까지, 각각 알파벳들의 개수를 재귀로 처리할 수 있다.

그리고 각각의 경우에는 단순 팩토리얼로 계산이 가능하다.

지적 및 질문 환영