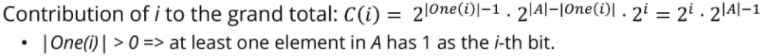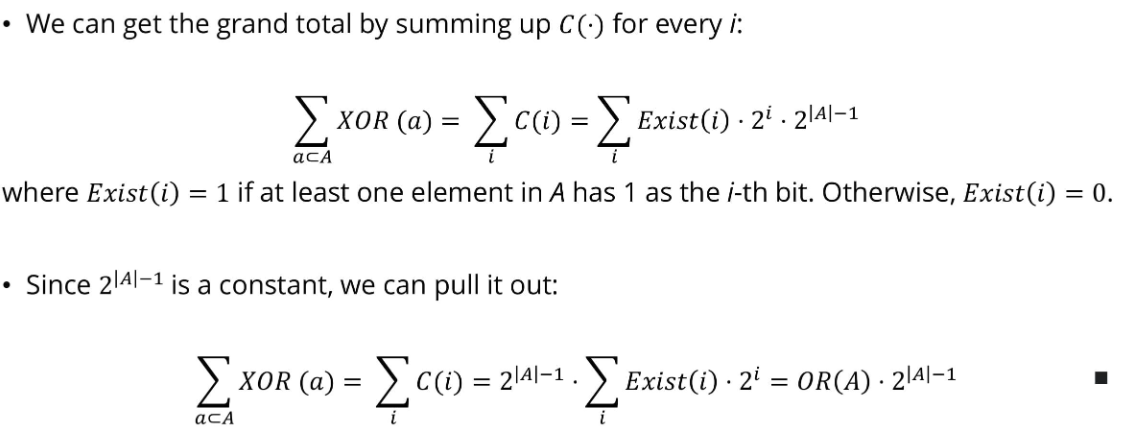Intuition

모든 subset의 xor을 체크해야하기 때문에 문제의 description에서 부터 모든 경우의 수를 확인해야 함을 알 수 있다. 이를 위해 재귀를 고려해보았다.

Approach

각 원소는 있거나(1), 없거나(0) 둘 중에 하나의 경우이다.

앞에서부터 0또는 1을 넣어주며 모든 경우를 확인할 수 있다.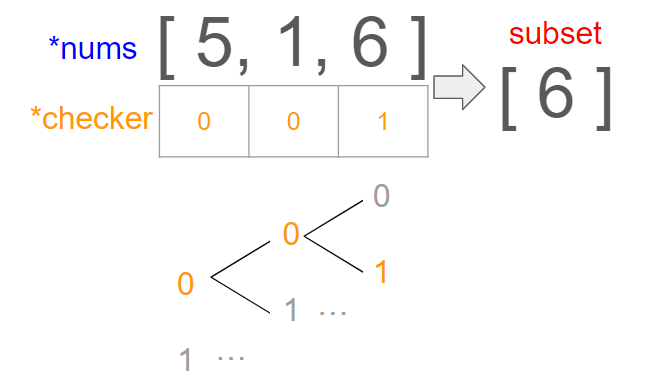

#include <stdlib.h>

int subsetXORSum(int* nums, int numsSize) {
    int* checker=(int*)malloc(sizeof(int)*numsSize);
    for (int i=0;i<numsSize;i++) checker[i]=0;
    
    return subset(0,numsSize,nums,checker);
}

int subset(int i, int numsSize, int* nums, int* checker){
    int ret=0;

    if (i==numsSize){
		//XOR 체크 파트
    }

    checker[i]=0;
    ret+=subset(i+1,numsSize,nums,checker);
    checker[i]=1;
    ret+=subset(i+1,numsSize,nums,checker);

    return ret;
}

Base case에 도달했을 때에는 xor연산을 통해 그 값을 반환해주면 된다.

    if (i==numsSize){
        int pre=0;
        for (int j=0;j<numsSize;j++){
            if (checker[j]){
                pre=pre^nums[j];
            } 
        }
        return pre;
    }

Solution

#include <stdlib.h>

int subsetXORSum(int* nums, int numsSize) {
    int* checker=(int*)malloc(sizeof(int)*numsSize);
    for (int i=0;i<numsSize;i++) checker[i]=0;
    
    return subset(0,numsSize,nums,checker);
}

int subset(int i, int numsSize, int* nums, int* checker){
    int ret=0;

    if (i==numsSize){
        int pre=0;
        for (int j=0;j<numsSize;j++){
            if (checker[j]){
                pre=pre^nums[j];
            } 
        }
        return pre;
    }

    checker[i]=0;
    ret+=subset(i+1,numsSize,nums,checker);
    checker[i]=1;
    ret+=subset(i+1,numsSize,nums,checker);

    return ret;
}

Complexity

Time Complexity

모든 경우의 수를 확인하는 과정에서 branch가 2개씩 깊이n만큼 발생한다. 계산하면, $O(2^N)$

Space Complexity

$O(N)$

교수님 풀이1

매개변수 자체에서 xor연산을 수행하는 방식이다.

#include <stdlib.h>

int subsetXORSum(int* nums, int numsSize) {    
    return subset(0,numsSize,nums,0);
}

int subset(int i, int numsSize, int* nums, int currentTotal){
    if (i==numsSize) return currentTotal;
    int total1=subset(i+1,numsSize,nums,currentTotal);
    int total2=subset(i+1,numsSize,nums,currentTotal^nums[i]);
    return total1+total2;
}

교수님 풀이2

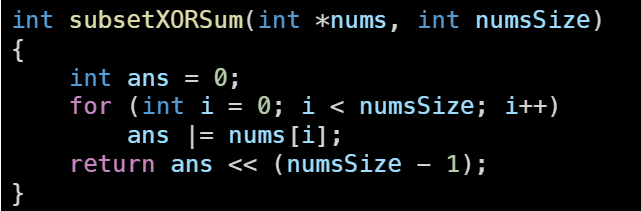
nums배열의 모든 원소에 bitwise OR연산을 한다음 numsSize-1만큼 왼쪽 시프트해줌으로써도 구할 수 있다.

위 식을 증명해보겠다.

우선, 어떤 집합의 부분집합의 개수중, 짝수(0포함)개의 원소를 갖고 있는 부분집합과, 홀수개인 원소의 부분집합의 개수는 같다. 이에 대한 증명은 집합 [a,b,c] 에서 a가 포함된 부분집합들 {a}, {a,b} .. 는 각각 공집합, {b} .. 로 1대1대응된다는 사실로서 알 수 있다.

또는, 어떤 집합에서 짝수(0포함)개의 원소를 갖는 부분집합의 개수는 $_nC_0+_nC_2+\cdots$, 홀수개는 $_nC_1+_nC_3+\cdots$으로 표현할 수 있는데 이는 이항계수의 성질에 의해 같음이 알려져있다.

집합A에 대해서 i번째 bit가 각각 1인 원소와 0인 원소로 이루어진 집합 두 개를 만든다. 이때 XOR연산을 수행했을 때 값에 변화가 있으려면 One집합에서 홀수개를 뽑아야한다. 짝수개의 1을 XOR연산을 하게 되면 0이 나오기 때문이다. Zero집합은 XOR연산시 항상 0이 나오므로 몇 개를 뽑든 상관없다.

One집합에서 홀수개의 원소를 뽑는 경우의 수는 $2^{|One|-1}$, Zero집합에서 임의의 개수를 뽑는 경우의수는 $2^{|Zero|}$이다. 그런데, One집합과 Zero집합의 합집합은 전체집합이므로 $2^{|A|-|One|}$으로 표현할 수 있다.i번째 bit에서 XOR연산을 수행했을 때 1이 나오는 경우의 수는 아래와 같고,이때, i번째 bit이므로 그 값은 $2^i$씩 증가하여 아래와 같이 표현할 수 있다.

지적 및 질문 환영