Intuition
의 시간 복잡도 내에 문제를 해결해야 하기 때문에, 실제로 두 배열을 합치는 방식은 배제한다. 실제로 정렬을 수행하지 않으면서 median을 찾는 방법을 고안해야한다.
중앙값이 개의 원소들을 정렬했을 때 (또는 )에 있는 것을 고려하여 개수에 중점을 두고 풀이해본다.
Approach
[1,3,4,6][2,7,8]의 두 배열을 합치면 아래와 같은 결과가 나온다.
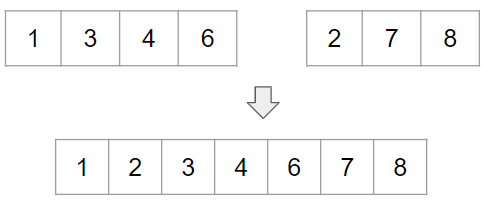 좀 더 자세하게 표시하면 아래와 같다.
좀 더 자세하게 표시하면 아래와 같다.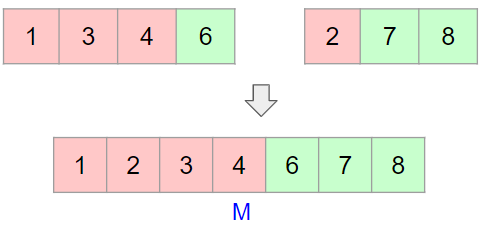 즉, 두 배열에서 임의의 개수만큼씩이 빨간 부분에 해당되고 나머지 부분들은 초록 부분에 해당된다는 것이다.
즉, 두 배열에서 임의의 개수만큼씩이 빨간 부분에 해당되고 나머지 부분들은 초록 부분에 해당된다는 것이다.
이때,
1. 합쳐진 배열에서 빨간부분의 개수는 에 구할 수 있다.
2. 그에 따라, nums1에서의 빨간부분의 개수가 정해지면 nums2에서의 빨간부분 개수도 자동으로 정해진다.
이어지는 내용에서 더 자세히 살펴보겠다.
합쳐진 배열이 홀수개인 경우와 짝수개인 경우를, 빨간부분의 인덱스 i와j를 활용하여 각각 표시해보면 아래와 같다.
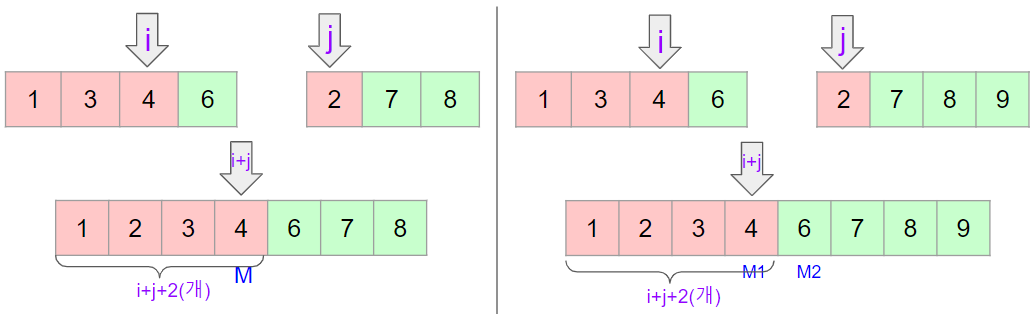
전자와 후자모두 인덱스 i와j는 2와0이다. 빨간색 부분의 개수는 각각의 인덱스에 +1씩을 하여 i+j+2 즉, 2+0+2(개) 가 된다.
빨간 부분의 개수는 두 배열의 사이즈를 통해서도 구할 수 있다.
홀수인 경우와 짝수인 경우 모두, 빨간부분이 M또는 M1을 포함하도록 설계하기 위해 빨간부분의 개수는 가 아닌, 로 구한다.
①,②에서
(개)
(개)
인덱스 의 값을 구하려면 을 해준다.
임의의 가 설정 되었을 때
그렇다면 임의의 i와 j가 설정되었을 때, 그것이 올바른 i와j인지 판단하려면 어떻게 해야할까.
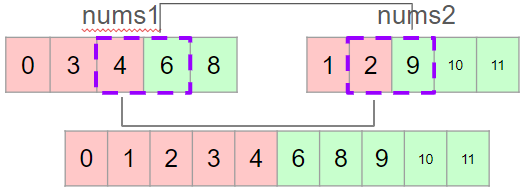
빨간 부분과 초록부분이 어떻게 정렬되는지는 우리는 실제로 신경쓰지 않는다. 다만, 제대로 i와j가 설정되었는지 판단하기 위해 빨간부분의 최댓값보다 초록부분의 최솟값이 더 큰지만 확인해주면 된다.
물론, 올바른 i와 j가 아닌것으로 판명났을 때에는 조정이 필요하다.
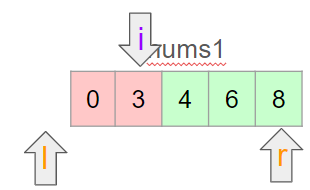
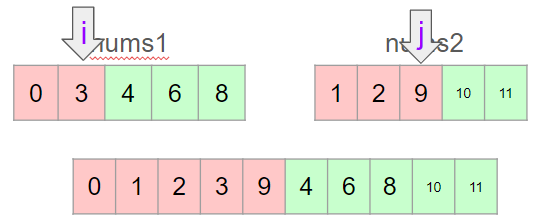 위와 같이 i의 값이 너무 작은 경우에는 그 값을 크게 해주어야 하는데, 얼마나 크게 해줄지를 결정해야한다. 우리는 여기에 이진탐색을 적용한다.
위와 같이 i의 값이 너무 작은 경우에는 그 값을 크게 해주어야 하는데, 얼마나 크게 해줄지를 결정해야한다. 우리는 여기에 이진탐색을 적용한다.
이때, 배열에서 한개도 빨간부분에 포함되지 않는 경우도 존재하기 때문에 이를 인덱스 -1로 나타내기로 한다.
i가 1인 경우 nums2의 빨간부분 최대값9와 nums1의 초록부분 최솟값4가 대소관계가 맞지 않는다.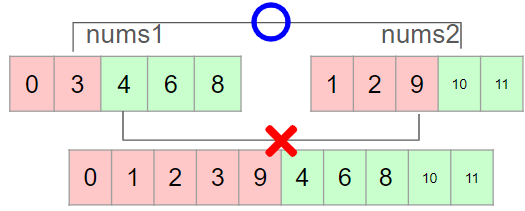
이 경우 l을 i+1로 옮겨 이진탐색을 지속한다.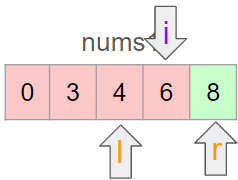 이번에는 i를 줄여줘야 하므로 r을 i-1로 설정함으로써 정답을 찾을 수 있다.
이번에는 i를 줄여줘야 하므로 r을 i-1로 설정함으로써 정답을 찾을 수 있다.
지금까지 설명한 부분을 코드로 작성하면 아래와 같다.
...
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
...
int l=-1, r=nums1Size-1; // -1은 안쓴다는 뜻
double res;
while(1){
int i=l+(r-l)/2;
int j=(nums1Size+nums2Size+1)/2-i-2;
...
if(...&&nums1[i]>nums2[j+1]){
r=i-1;
continue;
}
if(...&&nums2[j]>nums1[i+1]){
l=i+1;
continue;
}
else{
// 올바른 i,j 일 때
}
...
}
return res;
}배열에 접근할 때
배열에 접근할 때에는 유효한 인덱스인지를 체크해줘야한다.
우선 i와 j모두 -1부터 numsSize-1까지만이 유효하다.
그런데 i의 경우에는 이진탐색에 의해 통제하기 때문에 유효한 범위에서 벗어날 일이 없다.
j의 경우는 i의 값에 따라 -1보다 작아지거나 nums2Size의 값 이상으로 커지는 경우가 존재한다.
전자는 i의 값이 작아지게, 후자는 i의 값이 커지게 이분탐색함으로써 값을 조정한다.
...
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
...
int l=-1, r=nums1Size-1; // -1은 안쓴다는 뜻
double res;
while(1){
int i=l+(r-l)/2;
int j=(nums1Size+nums2Size+1)/2-i-2;
/* 추가된 코드 */
if(j<-1){
r=i-1;
continue;
}
if(j>=nums2Size){
l=i+1;
continue;
}
/* 추가된 코드 */
if(...&&nums1[i]>nums2[j+1]){
r=i-1;
continue;
}
if(...&&nums2[j]>nums1[i+1]){
l=i+1;
continue;
}
else{
// 올바른 i,j 일 때
}
...
}
return res;
}
그러나 유효한 값임에도 불구하고 -1이라는 인덱스는 우리가 해당 배열을 사용하지 않을 때를 가정한 가상의 인덱스이기 때문에 따로 처리를 해줘야한다. 추가적으로 j+1이나 i+1 또한 존재하지 않는 케이스를 대비해야한다.
예를 들어, 아래 그림에서 nums2의 빨간부분의 최댓값과 nums1의 초록부분의 최솟값을 비교해야하는데 j는 -1, i+1은 유효하지 않은 인덱스로 비교가 불가능하다.
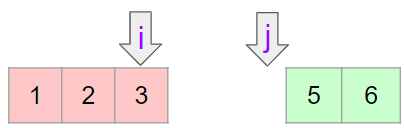 그러나, 문제상황에서 비교대상 둘 중 하나 이상이 없는 것은 적절한 i와 j가 됨에 문제가 되지 않음을 뜻한다.
그러나, 문제상황에서 비교대상 둘 중 하나 이상이 없는 것은 적절한 i와 j가 됨에 문제가 되지 않음을 뜻한다.
...
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
...
int l=-1, r=nums1Size-1; // -1은 안쓴다는 뜻
double res;
while(1){
int i=l+(r-l)/2;
int j=(nums1Size+nums2Size+1)/2-i-2;
if(j<-1){
r=i-1;
continue;
}
if(j>=nums2Size){
l=i+1;
continue;
}
if(i!=-1&&j+1!=nums2Size&&nums1[i]>nums2[j+1]){ // 추가된 코드
r=i-1;
continue;
}
if(ㅊnums2[j]>nums1[i+1]){ // 추가된 코드
l=i+1;
continue;
}
else{
// 올바른 i,j 일 때
}
...
}
return res;
}중앙값 찾기
올바른 i와 j를 찾았다면 이제 median 값을 구하는 것만 남았다.
홀수개인 경우에는 빨간색 부분의 최댓값만 구하면 된다.
짝수개인 경우에는 초록색 부분의 최솟값도 구하여 두 값의 평균을 구한다.
else{
if((nums1Size+nums2Size)%2){ // odd
int max=-1000001;
if(i!=-1) max=MAX(max,nums1[i]);
if(j!=-1) max=MAX(max,nums2[j]);
res=max;
}
else{ // even
int max=-1000001;
if(i!=-1) max=MAX(max,nums1[i]);
if(j!=-1) max=MAX(max,nums2[j]);
int min=1000001;
if(i+1!=nums1Size) min=MIN(min,nums1[i+1]);
if(j+1!=nums2Size) min=MIN(min,nums2[j+1]);
res=(max+min)/(double)2;
}
break;
}더 작은 배열에서 탐색하기
마지막으로, nums1과 nums2 중 더 작은 배열을 항상 nums1으로 만들어준다.
이진탐색의 범위가 줄어드므로 시간복잡도도 줄어든다.
#define MAX(a,b) ((a)>(b)?(a):(b))
#define MIN(a,b) ((a)<(b)?(a):(b))
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
/* 추가된 코드 */
if (nums1Size>nums2Size){
int* tmp=nums1;
nums1=nums2;
nums2=tmp;
int tmp2=nums1Size;
nums1Size=nums2Size;
nums2Size=tmp2;
}
/* 추가된 코드 */
int l=-1, r=nums1Size-1; // -1은 안쓴다는 뜻
double res;
while(1){
int i=l+(r-l)/2;
int j=(nums1Size+nums2Size+1)/2-i-2;
if(j<-1){
r=i-1;
continue;
}
if(j>=nums2Size){
l=i+1;
continue;
}
if(i!=-1&&j+1!=nums2Size&&nums1[i]>nums2[j+1]){
r=i-1;
continue;
}
if(j!=-1&&i+1!=nums1Size&&nums2[j]>nums1[i+1]){
l=i+1;
continue;
}
else{
if((nums1Size+nums2Size)%2){ // odd
int max=-1000001;
if(i!=-1) max=MAX(max,nums1[i]);
if(j!=-1) max=MAX(max,nums2[j]);
res=max;
}
else{ // even
int max=-1000001;
if(i!=-1) max=MAX(max,nums1[i]);
if(j!=-1) max=MAX(max,nums2[j]);
int min=1000001;
if(i+1!=nums1Size) min=MIN(min,nums1[i+1]);
if(j+1!=nums2Size) min=MIN(min,nums2[j+1]);
res=(max+min)/(double)2;
}
break;
}
}
return res;
}Solution
#define MAX(a,b) ((a)>(b)?(a):(b))
#define MIN(a,b) ((a)<(b)?(a):(b))
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
if (nums1Size>nums2Size){
int* tmp=nums1; nums1=nums2; nums2=tmp;
int tmp2=nums1Size; nums1Size=nums2Size; nums2Size=tmp2;
}
int l=-1, r=nums1Size-1; // -1은 안쓴다는 뜻
while(1){
int i=l+(r-l)/2;
int j=(nums1Size+nums2Size+1)/2-i-2;
if(j<-1){ r=i-1; continue; }
if(j>=nums2Size){ l=i+1; continue; }
if(i!=-1&&j+1!=nums2Size&&nums1[i]>nums2[j+1]){ r=i-1; continue; }
if(j!=-1&&i+1!=nums1Size&&nums2[j]>nums1[i+1]){ l=i+1; continue; }
else{
int max=-1000001;
if(i!=-1) max=MAX(max,nums1[i]);
if(j!=-1) max=MAX(max,nums2[j]);
if((nums1Size+nums2Size)%2) return max;
int min=1000001;
if(i+1!=nums1Size) min=MIN(min,nums1[i+1]);
if(j+1!=nums2Size) min=MIN(min,nums2[j+1]);
return (max+min)/(double)2;
break;
}
}
return 0; // 여기까지 올 일은 없다.
}Time complexity
nums1과 nums2중 더 작은 배열에서 이분탐색을 진행한다.