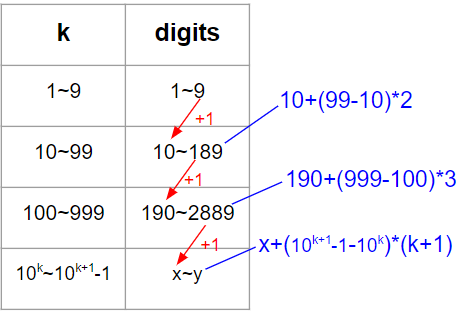
Intuition

이진탐색으로 output후보를 탐색하면서, 그때그때마다 해당 후보가 정답범위에 있는지를 체크하기로 했다.

Approach

예를 들어 12는 10에서 2만큼 차이가 나고, 또 두자리수이기 때문에 10에서 1씩 커질때마다 digits는 2씩 증가한다. 따라서 10+(12-10)2=14 즉, 12에서 1은 14번째 자리수이다.

또 다른 예시로 99는 10+(99-10)2=188 즉, 각각 188번째, 189번째 수가 될 것이다.
이어서 100은 99의 다음 숫자이므로, 100의 1은 190번째 수가 된다.
마지막 예시로 777은 190+(777-100)3 으로 계산할 수 있다.

위와 같이 일반화할 수 있다.

즉, 우리가 어떤 수 k의 자리수(ex. 두자리수, 세자리수)와 해당 자리수의 시작하는 출발digit(?)(위 표에서 1,10,190,x에 해당하는 부분)만 알고있다면 $O(1)$만에 k의 digits을 구할 수 있다는 것을 알 수 있다는 것이다.

digits을 구하고나서, n에서 digits을 뺀 값이 자리수보다 작다면 어떤 숫자 k에 정답이 존재하는 것이다.
예를 들어, n이 542이고 이진탐색 과정으로 나온 후보 숫자 k가 217이다.
190+(217-100)3=541이므로 217은 각각 541번째, 542번째, 543번째 digits이다.
{n}-{digits}=542-541=1<{자리수}=3이므로 k에 정답인 digits이 존재함을 알 수 있다.
즉, {자리수}-({n}-{digits})=3-(542-541)=2이므로 일의 자리부터 두번째 자리에 정답이 위치하는 것을 알 수 있다.
두번째 자리 숫자를 구하기 위해 217을 10으로 한번 나누고 %10연산을 한 번 취해주면 정답인 1을 구할 수 있게 된다.

Solution

long startArray[10]; // 위의 표에서 x에 해당하는 부분을 담는 배열

int check(int mid, int n){
    int digits=0; // 자리수를 담는 변수 (ex. 두자리수, 세자리수 ...)
    int tmp=mid;
    while (tmp!=0){
        tmp/=10;
        digits++;
    }

    int ten=1; 
    tmp=digits;
    while (--tmp) ten*=10; // 자리수만큼 10의 제곱을 만들어주기
    long calc=startArray[digits-1]+((long)mid-ten)*digits;

    if (calc>n) return 0; 
    if (n-calc<digits) return digits-(n-calc); // 정답이 존재하는 숫자일 경우
    else return -1;
}

void startArrayFunc(){ // 위의 표에서 x에 해당하는 부분을 미리 계산하는 함수
    startArray[0]=1;
    long nine=9;
    long ten=1;
    for (int i=1;i<10;i++,nine=nine*10+9,ten*=10){
        startArray[i]=(startArray[i-1]+(nine-ten)*(long)i)+i;
    }
}

int findNthDigit(int n) {
    int m=1, M=n;
    int mid, checkRet;
    startArrayFunc();

    while (m<=M){
        mid=m+(M-m)/2;
        checkRet=check(mid,n);
        if (checkRet==0) M=mid-1;
        else if (checkRet==-1) m=mid+1;
        else break;
    }

	/*
    {자리수}-({n}-{digits})번째에 정답인 수가 위치
    */
    for (int i=0;i<checkRet-1;i++) mid/=10;
    return mid%10;
}

Time Complexity

startArrayFunc는 최초 실행시 딱 한 번 수행된다.
이진탐색과 함께 매번 check함수가 호출되지만 기껏해야 반복문은 10번돈다.
따라서,이진탐색의 시간복잡도만 유의미한 영향을 미칠 것으로 예상한다.
$O(logN)$

지적 및 질문 환영