수학
1.Taylor Series, Taylor Theorem and Maclaurin Series
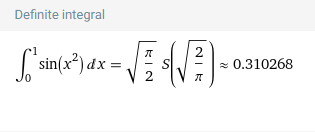
에라토스테네스의 체의 시간복잡도를 증명하기 위해 공부하다보니 테일러 급수에 대한 개념이 필요해서 포스팅을 하게 되었다. 테일러 급수와 테일러 정리란? 가령, 우리가 $\int_{0}^{1}\sin(x^2)dx$을 계산해야 한다고 가정해보자. 아마 쉽지 않을 것이다. 그
2023년 4월 4일
2.sinx/x의 극한

테일러 급수의 예시에 대해 공부하다가 고등수준에서의 증명이 궁금해서 포스팅하게 되었다. 그림 출처 : Gribozavr, Public domain, via Wikimedia Commons 부채꼴 $ABC$와 $\overline{AC}$의 연장선과 점$B$에서 수
2023년 4월 7일
3.Basel Problem

에라토스테네스의 체의 시간복잡도 증명과정에서 소수의 역수들의 합에 대해 공부하는 과정에서 비슷하지만 다른 형태인 자연수들의 제곱의 역수의 합 문제를 발견하게 되었는데, $\\sin x$ 식의 변형이 흥미로워서 포스팅해보게 되었다.문제는 매우 간단하다.다음 급수의 값을
2023년 4월 8일