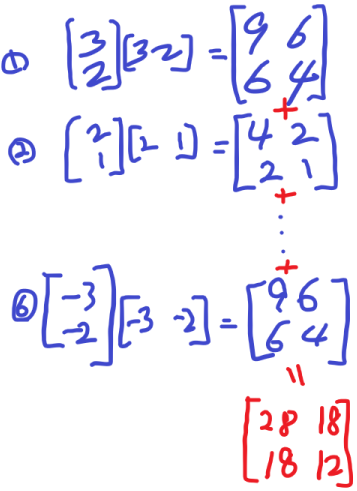SVC, PCA

특이값 분해(SVC, Singular Value Decomposition)

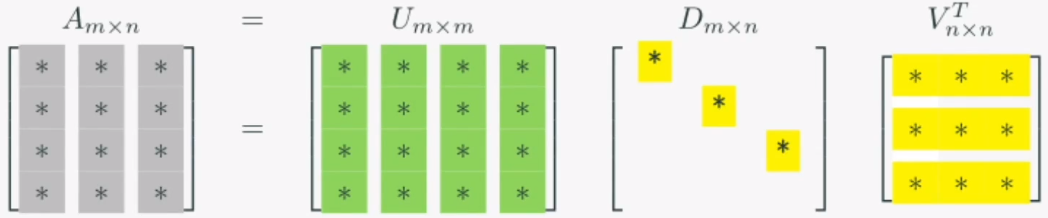
• U: m × m 회전행렬 (정규직교행렬)
• D: m × n 확대축소 (확대축소 크기에 따른 정렬 형태)
• V: n × n 회전행렬 (정규직교행렬)

SVD의 과정

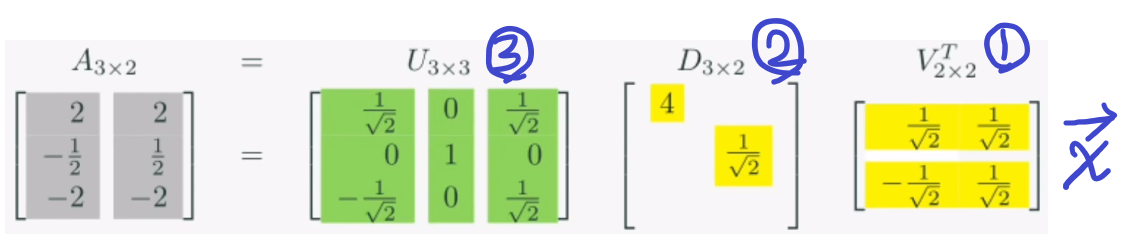
벡터x에 A를 연산하는 과정을 특이값분해를 통해 분석해봅시다.
연산은 V -> D -> U의 순서로 진행됩니다.

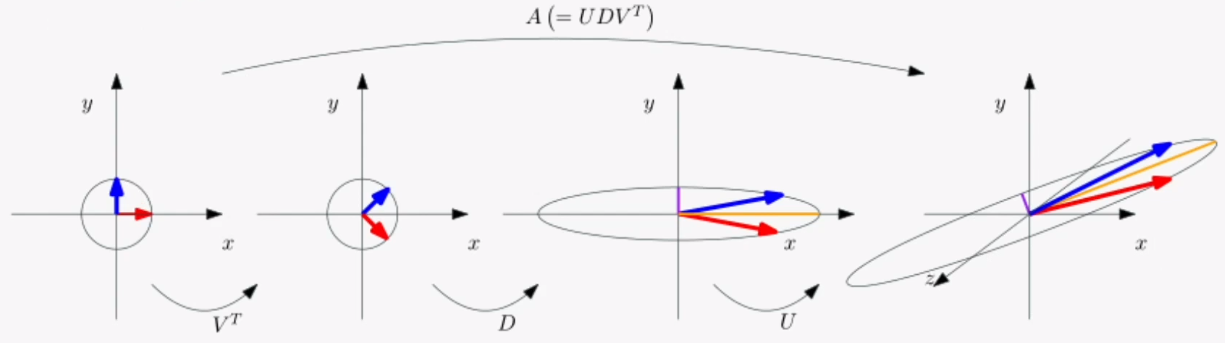
1. V는 시계방향으로 45도 회전하는 함수이다.
2. D는 x방향으로 4배, y방향으로 1/sqrt(2)배만큼 확대축소하는 함수이다.
3. U는 y축을 기준으로 45도 회전하는 함수이다.

SVD의 근사

만약 SVD 계산을 단순화 하고싶다면 근사치를 계산할수도 있습니다.
바로 D에서 작게 증폭되는 값을 버리는 방법으로요!

위 식에서 D에 4만 남겨두게 되면, U는 1열만 필요하고, V는 1행만 필요합니다.

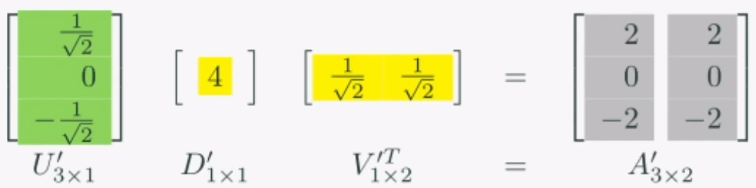
결과적으로 위와같은 식이 되어 계산이 매우 편해집니다!
이 연산의 기하학적 의미를 알아보면,

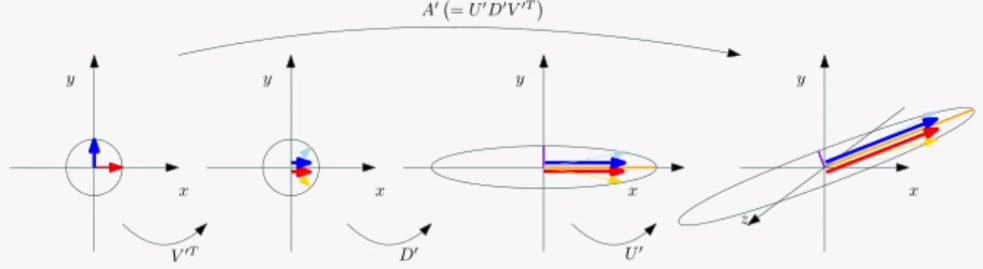
1. y축으로 증폭된 값을 버리고, x축으로의 수선의 발(곱셈 연산)을 가지고 갑니다.
2. x축으로만 4배 증폭합니다.
3. y축을 기준으로 회전하는것처럼 보이지만, 사실 곱셈연산

주성분분석(PCA, principal Component Analysis)

데이터의 공분산행렬을 찾기위한 직교분해입니다.
참고로, 데이터의 중심 m 과 공분산행렬 C는 아래와 같이 구합니다.

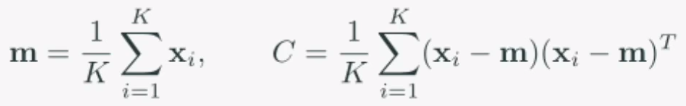
PCA는 아래와 같이 나타냅니다.

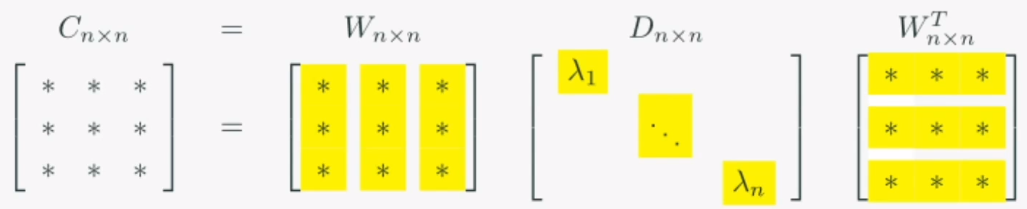
여기서 각각의 의미를 살펴보면,

• W의 각 열벡터들은 분포들의 주성분 방향과 같습니다.
• D의 각 요소들은, 그 주성분의 크기와 같습니다.
• 여기서 주성분은 아래의 그림에 보이는 화살표입니다.
  
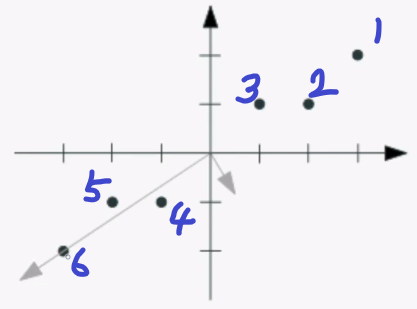
  주성분은 원래 아래의 좌측 값입니다.
  이 값을 구하는 방법은 모든 행렬값을 더해서 그 갯수로 나눈 값입니다.
  그런데 PCA분석을 이용해서 주성분을 분석할 수 있습니다.
  
  <주성분 구하는법>