수학

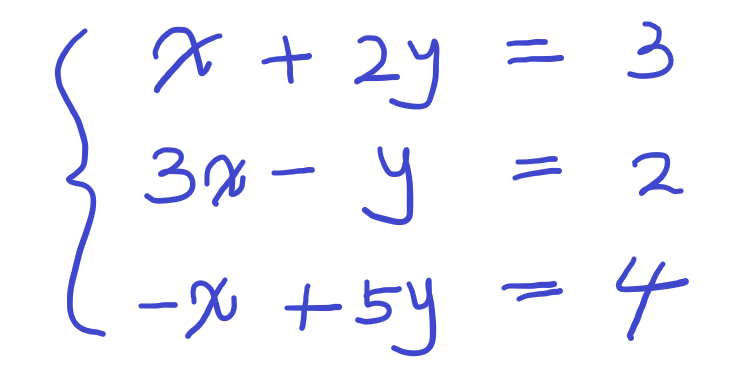
a x = b를 선형 방정식이라고 한다.여러 개의 선형 방정식을 연립하면 아래와 같다.연립되는 식이 많아질수록 복잡해진다.그래서 더 단순화하고 정형화 하기 위해 새로운 방법을 고안했다.행렬을 사용해서 어떤 선형 연립식이든 A x = b의 형태로 만드는 방법이다.위에서

선형 시스템의 해를 구하는 대표적인 방법이다.1\. Forward elimination(전방소거법)2\. back-substitution(후방대입법)의 순서로 진행된다.이랬던 선형시스템을이렇게 바꿔주는 작업이다.전방소거법을 수행하면 두 가지 장점이 있다.계산이 쉬워진다

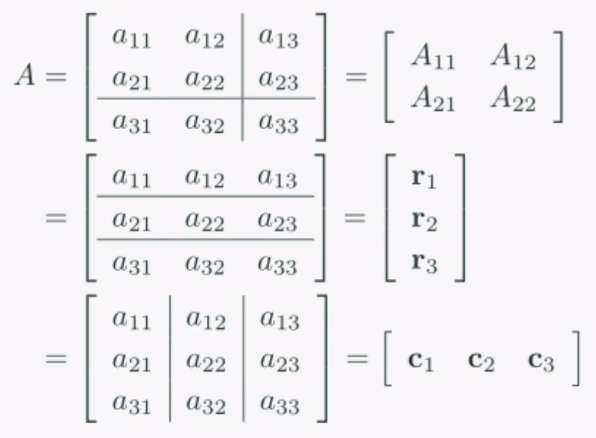
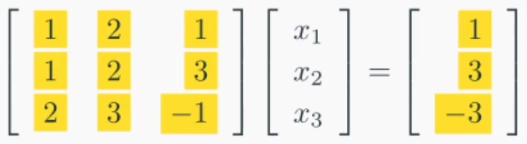
두 행렬의 곱으로 만들어지는 행렬 C 의 각 성분들은 독립적이라는 것을 뜻한다.무슨 말이냐면, C11을 철수가 계산하고 C12를 영희가 계산해도 된다는 소리다.컴퓨터가 행렬 계산을 할 때, 병렬연산을 사용하여 더욱 빠르게 계산을 할 수 있다.텐서는 데이터의 배열을 의미

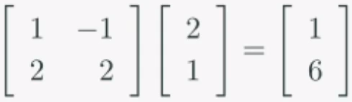
선형시스템 Ax=b 가 있을 때, 행렬A를 좌표계로 보고 벡터x와 b를 좌표값으로 보는 방법입니다.예를들어,위와 같은 식에서 b는 앞에 항등행렬을 곱한것과 같습니다.그리고 항등행렬을 좌표계로 보면, xy좌표계와 같습니다. 따라서이런 벡터모양을 가지게 됩니다.이번에는 A

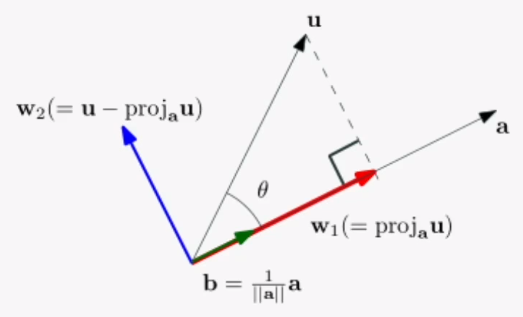
벡터 a에 벡터 u를 투영시키면, 벡터 w1이 됩니다.w2는 u를 a에 투영하고 남은 벡터라고 하여 보완벡터(complement vector)라고 합니다.직교행렬은 행렬의 열벡터들이 서로 직각을 이루고 있는 행렬을 말합니다.여기에 각 열벡터들의 길이가 1일 때, 정규직

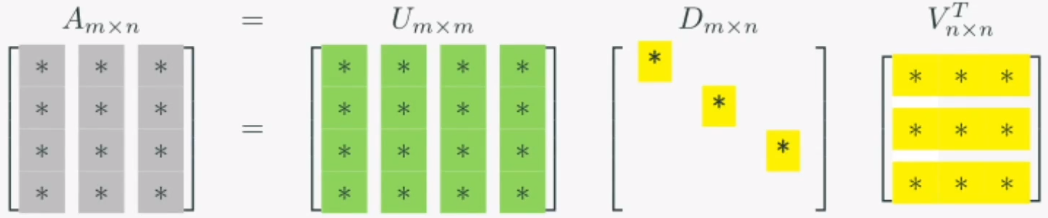
U: m × m 회전행렬 (정규직교행렬)D: m × n 확대축소 (확대축소 크기에 따른 정렬 형태)V: n × n 회전행렬 (정규직교행렬)벡터x에 A를 연산하는 과정을 특이값분해를 통해 분석해봅시다.연산은 V -> D -> U의 순서로 진행됩니다.1\. V는 시계방향

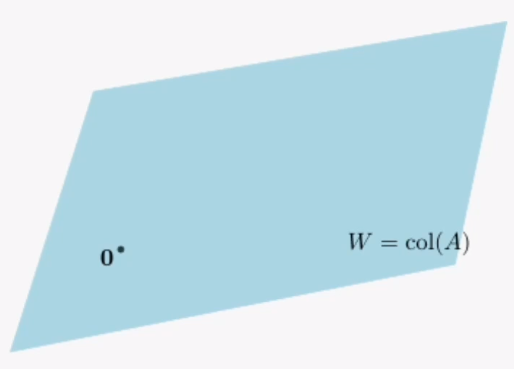
어떤 공간 안에서 아무리 벡터들을 더하거나 스칼라곱을 해도 벗어날 수 없는 공간을 말합니다.행렬 A의 모든 열벡터로 만들어진 벡터공간을 열벡터라 합니다.열벡터들로 가능한 모든 선형조합을 집합으로 모으면 구할 수 있습니다.만약 선형시스템 Ax = b가 해가 없으면, 아래

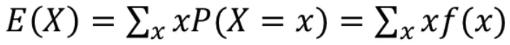
동전 10개를 던지는 실험에서 동전 앞면이 나온 수를 뜻함보통 X나 Y같은 대문자로 표시한다.다음과 같이 분류한다.이산확률변수: 셀 수 있는 경우 (동전 10개 던질 때 앞면이 나온 수, 4개)연속확률변수: 셀 수 없는 경우 (어느 학교에서의 남학생의 수, 171.23

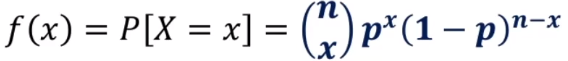
이항확률분포의 확률분포이다.이항확률분포란? n번의 베르누이 시행에서 성공의 횟수베르누이시행이란? 동전던지기처럼 결과가 두 개뿐인 실험 10개의 동전을 던졌을 때 앞면이 x개 나오는 확률: python에서 scipy.stats 모듈로 구할 수 있다.이항분포의 평균, 분산

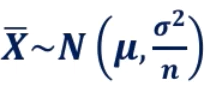
통계량의 확률분포이다.통계량: 표본평균, 표본분산 등모집단이 정규분포를 이룰 때 표본평균은 아래와 같이 구한다. (표본 분포도 정규분포이다.)python으로 구하는 법은모집단이 표본분포가 아닐 때 사용할 수 있는 표본 분포표본 평균은 아래와 같이 구한다.n이 충분히 커

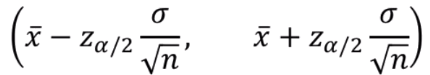
특정 지점에서의 평균 추정값이다.표본평균이 점 추정값이 된다.아래와 같이 간단하게 구할 수 있다.특정 %만큼 신뢰할 수 있는 구간을 파악할 때 활용한다.다음과 같이 모평균의 100(1 - a)% 신뢰구간을 구할 수 있다.n이 충분히 큰 중심극한분포에서는 다음과 같이 구

가설검정이란?만약 학생수가 1000명인 고등학교에서 30명의 랜덤하게 학생을 뽑아 키를 쟀더니 평균 172cm였다.그러면 전체 학생들의 키 평균이 170cm 이상이라고 할 수 있을까?에 대한 확률을 검정하는 것이다.모평균과 표본평균이 같을 가능성을 놓고, 특정 확률 이

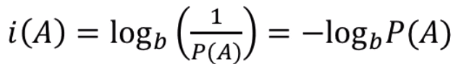
확률이 낮은 사건일수록 값어치있는 정보(내포하고 있는 정보가 많다)라는 의미이다.여기서 정보의 단위 b는등이 있고, 일반적으로 2를 많이 사용한다.자기정보는 아래의 특성이 있다.자기정보의 평균이다.K개의 사건이 일어났을 때 엔트로피는 아래와 같은 특성이 있다.엔트로피는