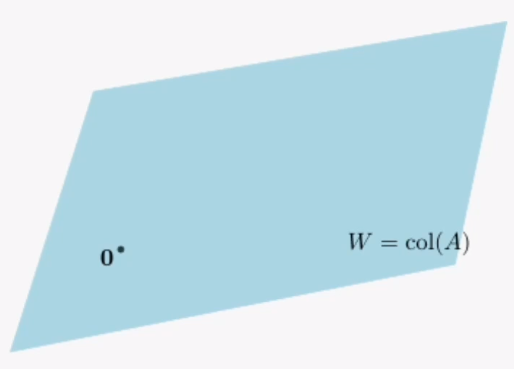
벡터공간이란?
어떤 공간 안에서 아무리 벡터들을 더하거나 스칼라곱을 해도 벗어날 수 없는 공간을 말합니다.
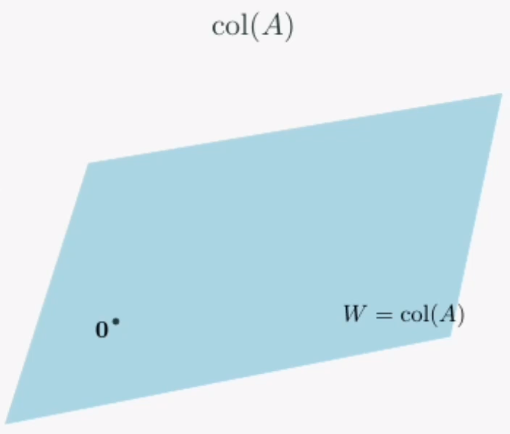
열공간의 의미
행렬 A의 모든 열벡터로 만들어진 벡터공간을 열벡터라 합니다.
열벡터들로 가능한 모든 선형조합을 집합으로 모으면 구할 수 있습니다.
만약 선형시스템 Ax = b가 해가 없으면, 아래와 같은 형국이 만들어집니다.
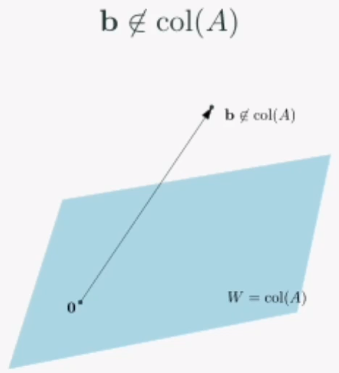
이렇게 선형시스템이 해가 있는지 없는지를 구할 수 있습니다.
최소제곱법이란?
만약 Ax = b가 해가 없다고 해도 가까운 해라도 구하고싶다!! 라고 할 때 사용할 수 있는 방법입니다.
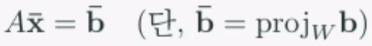
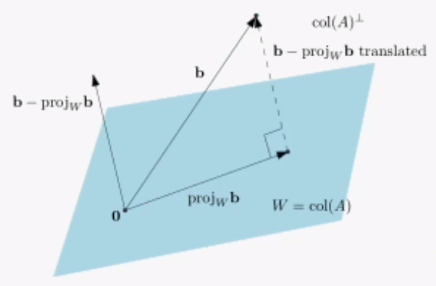
원래목표 b와 새로운목표 b'의 차이 (b-b')의 제곱을 최소화하는 의미라서 이름이 최소제곱법입니다.
구하는 방법
Ax = b의 양변에 AT를 곱하면 됩니다.
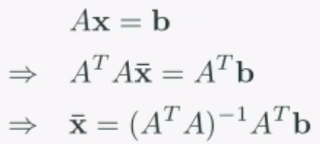
활용
선형회귀 문제에 응용할 수 있습니다.
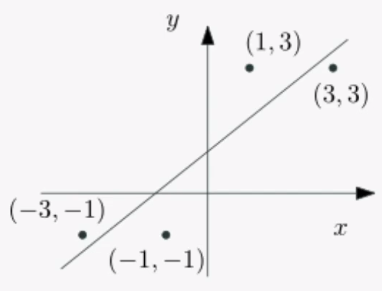
위의 예시에서는 네 지점을 모두 지나는 직선은 없습니다.
아래는 y = mx + b에 (x, y)를 대입했을 때의 값들을 행렬식으로 만든 것입니다.
ex) (-3)m + (1)b = (-1)
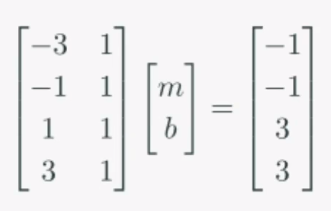
그래서 최소제곱법을 사용하면,
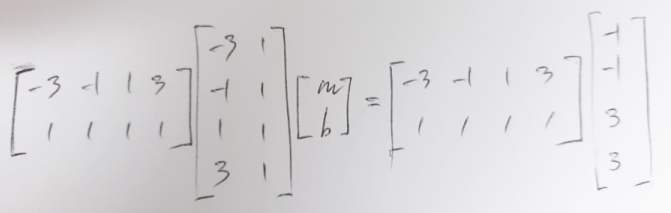
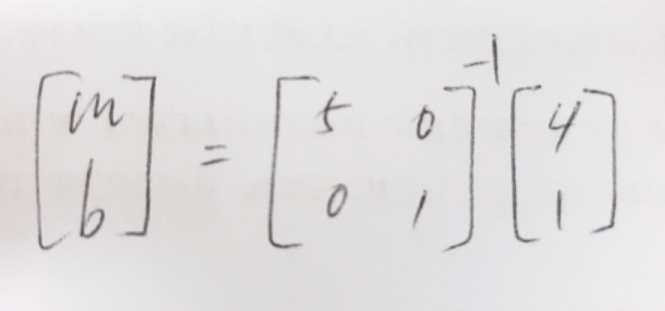
m = 4/5, b = 1 이므로
y = 4/5x + 1의 직선이 그려집니다.
열공하는 개발자입니다~~