교차 엔트로피

엔트로피

자기정보

확률이 낮은 사건일수록 값어치있는 정보(내포하고 있는 정보가 많다)라는 의미이다.

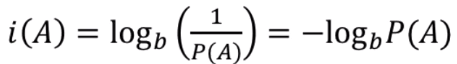
여기서 정보의 단위 b는

등이 있고, 일반적으로 2를 많이 사용한다.

자기정보는 아래의 특성이 있다.

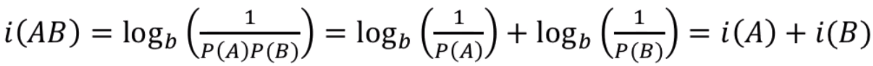
엔트로피란?

자기정보의 평균이다.

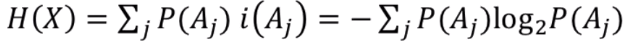
K개의 사건이 일어났을 때 엔트로피는 아래와 같은 특성이 있다.

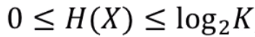
엔트로피는 다음과 같이 활용할 수 있다.

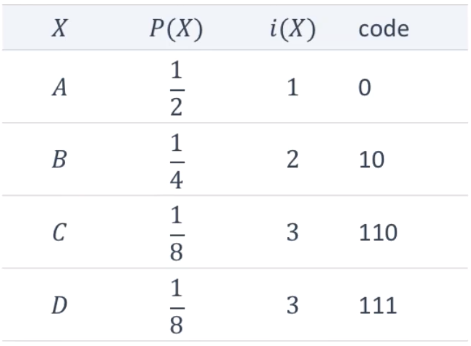
"ABCD"라는 데이터를 전송할 때,
일반적으로 전송하면 평균 2bit가 필요하다.
엔트로피를 이용해 압축하면, 평균 ΣP(X)i(X) = 7/4bit가 필요하다.

교차 엔트로피

교차엔트로피란?

P에 대한 확률분포 Q가 있을 때, Q가 P와 얼마나 비슷한지를 나타내는 의미가 있다.
위의 엔트로피 활용의 예 에서 P의 확률분포 Q가 있을 때, Q의 엔트로피를 구하면,

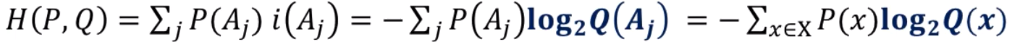
P일때가 최적해이므로, H(P, Q) >= H(P)이다.
Q가 P와 비슷할수록 H(P, Q)는 H(P)에 가까워진다.

손실함수

교차엔트로피는 기계학습에서 손실함수로 많이 사용된다.
특히, 분류문제에서의 손실함수로 사용되는데

부류문제란?

• 주어진 대상이 A인지 아닌지를 판단하는 문제
• 주어진 대상이 A B C 중 무엇인지 판단하는 문제

기계학습에서는 주어진 대상이 각 그룹에 속할 확률을 제공한다.
예: [0.8, 0.2] A일확률 80%, 아닐확률 20%
이 값이 정답인 [1.0, 0.0]과 얼마나 다른지 측정이 필요하다.

손실함수에는 여러 종류가 있는데, 그 중 대표적인 제곱합과 비교를 하면,

제곱합	교차엔트로피
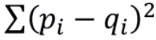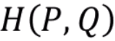확률이 다를수록 커짐	확률이 다를수록 커짐
학습속도 느림	학습속도 빠름
	분류문제에서 주로 이용

교차 엔트로피를 사용해서 손실함수를 구해보자.

p = [1, 0]이 정답일 때,

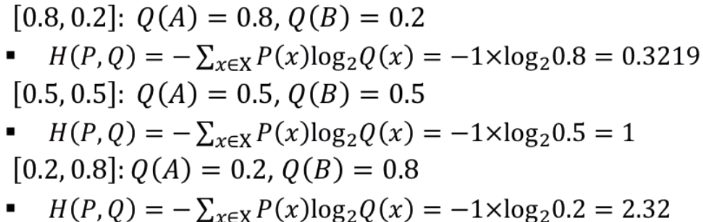
• [0.8, 0.2]일때 0.3219
• [0.5, 0.5]일때 1
• [0.2, 0.8]일때 2.32

이렇게 정답과 다를수록 손실계수가 커진다.

이를 python으로 계산하면,

import numpy as np

def crossentropy(P, Q):
  return sum([-P[i]*np.log2(Q[i]) for i in range(len(P))])

[crossentropy([1, 0], [1-i/10, i/10]) for i in range(1, 10)]

->
[0.15200309344504997,
 0.3219280948873623,
 0.5145731728297583,
 0.7369655941662062,
 1.0,
 1.3219280948873622,
 1.7369655941662059,
 2.3219280948873626,
 3.3219280948873626]

이렇게 구할 수 있다.