[알고리즘] PST-크루스칼(Kruskal) 알고리즘

Kruskal 알고리즘이란

탐욕적인 방법(greedy method) 을 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것

• 탐욕적인 방법
  - 결정을 해야 할 때마다 그 순간에 가장 좋다고 생각되는 것을 선택함으로써 최종적인 해답에 도달하는 것
  • 탐욕저긴 방법은 그 순간에는 최적이지만, 전체적인 관점에서 최적이라는 보장이 없기 때문에 반드시 검증해야 한다.
  • 다행히 Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명되어 있다.
  • 정리( G를 무방향 연결 그래프라 하자. Kruskal 알고리즘은 최소 비용 신장트리를 생성한다)
• MST가 1) 최소 비용의 간선으로 구성됨 2) 사이클을 포함하지 않음 의 조건에 근거하여 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택 한다.

Kruskal 알고리즘의 동작

1. 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
2. 정렬된 간선 리스트 중에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
   • 즉, 가장 낮은 가중치를 먼저 선택한다.
   • 사이클을 형성하는 간선을 제외한다.
3. 해당 간선을 현재의 MST의 집합에 추가한다.

• 한번에 하나씩 T에 간선을 추가해가면서 최소비용 신장트리 T를 구축
• T에 포함될 간선을 비용의 크기 순으로 선택
• 이미 T에 포함된 간선들과 사이클을 형성하지 않는 간선만을 T에 추가
• G는 연결되어 있고 n>0 개의 정점을 가지므로 정확히 n-1개의 간선만이 T에 포함됨

Kruskal 알고리즘의 구체적인 동작 과정

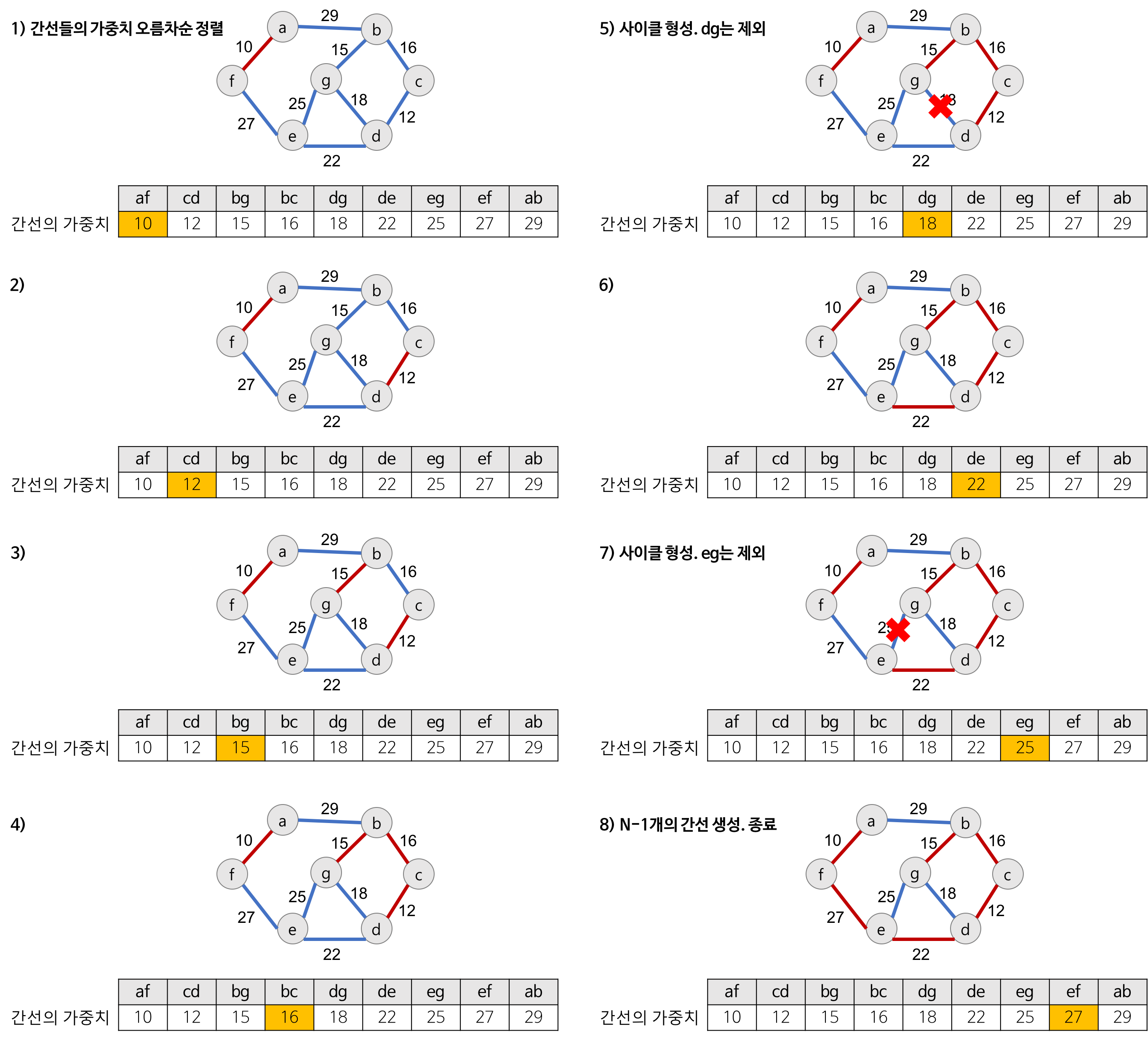
kruskal 알고리즘을 이용하여 MST를 만드는 과정

• 간선 선택을 기반 으로 하는 알고리즘
• 이전 단계에서 만들어진 신장트리와는 상관없이 무조건! 최소 간선 만을 선택하는 방법

주의!

• 다음 간선을 이미 선택된 간선들의 집합에 추가할 때 사이클을 생성하는지 체크!
• 새로운 간선이 이미 다른 경로에 의해 연결되어 있는 정점들을 연결할 때 사이클이 형성된다.
  - 즉, 추가할 새로운 간선이 양 끝 정점이 같은 집합에 속해 있으면 사이클이 형성된다.
• 사이클 생성 여부를 확인하는 방법
  - 추가하고자 하는 간선의 양 끝 정점이 같은 집합에 속해 있는 지를 먼저 검사해야 한다.
  • union-find 알고리즘 이용

Kruskal 알고리즘의 시간 복잡도

• union-find 알고리즘을 이용하면 Kruskal 알고리즘의 시간 복잡도는 간선들을 정렬하는 시간에 좌우된다.
• 즉, 간선 e개를 퀵 정렬과 같은 효율적인 알고리즘으로 정렬한다면
  - Kruskal 알고리즘의 시간 복잡도는 O(elog2e)이 된다.
• Prim 알고리즘의 시간 복잡도는 O(n^2) 이므로
  - 그래프 내에 적은 숫자의 간선만을 가지는 희소그래프의 경우 kruskal 알고리즘이 적합하고
  • 그래프에 간선이 많이 존재하는 밀집 그래프의 경우 prim알고리즘이 적합하다.

Kruskal 알고리즘의 구현

#include <iostream>
#include <vector>
#include <algorithm>
#define NODE 7
#define EDGE 9
using namespace std;

// 부모 노드를 가져옴, find 연산
int getParent(int parent[], int node) {
	if (parent[node] == node) {
		return node;
	}
	return getParent(parent, parent[node]);
}

//두 부모의 노드를 합침, 트리의 높이가 큰 쪽에 합침
int unionParent(int parent[], int x, int y) {
	x = getParent(parent, x);
	y = getParent(parent, y);
	if (x < y) {
		parent[y] = x;
		return x;
	}
	else {
		parent[x] = y;
		return y;
	}
}

//같은 부모 노드를 갖는지 확인
int findParent(int parent[], int x, int y) {
	x = getParent(parent, x);
	y = getParent(parent, y);

	if (x == y) {
		return 1;
	} // 같은 부모노드
	else {
		return 0;
	} // 다른 부모노드
}

//간선들의 정보
class Edge {
public:
	int node[2]; //양 끝 정점
	int distance;
	Edge(int x, int y, int distance) {
		this->node[0] = x;
		this->node[1] = y;
		this->distance = distance;
	}
	bool operator <(Edge &edge) {
		return this->distance < edge.distance;
	}
};

int main(int argc, char *argv[]) {

	vector<Edge> v;
	v.push_back(Edge(0, 1, 28));
	v.push_back(Edge(0, 5, 10));
	v.push_back(Edge(1, 2, 16));
	v.push_back(Edge(1, 6, 14));
	v.push_back(Edge(2, 3, 12));
	v.push_back(Edge(3, 4, 22));
	v.push_back(Edge(3, 6, 18));
	v.push_back(Edge(4, 5, 25));
	v.push_back(Edge(4, 6, 24));

	//거리를 오름차순으로 정렬
	sort(v.begin(), v.end());

	//초기화
	int parent[NODE];
	for (int i = 0; i < NODE; i++) {
		parent[i] = i;
	}

	int sum = 0;
	for (int i = 0; i < v.size(); i++) {
		if(!findParent(parent, v[i].node[0], v[i].node[1])){
		 //사이클이 생기지 않는 경우(다른 부모를 갖는 경우)
			sum += v[i].distance;
		// 연결을 하고 나면, 같은 부모를 갖게 되므로
			unionParent(parent, v[i].node[0], v[i].node[1]);
		} //end if
			
	}//end for

	//결과 확인
	cout << sum;
	return 0;
}