VAE를 처음 접했을 때, ELBO term을 최대화하는 게 왜 KL Divergence를 최소화하는 문제가 되는 건지, VAE가 왜 Likelihood를 최대화하는 Generative Model인지 잘 이해하지 못했다. 이번주에 VAE를 복습하며 이활석님의 오토인코더의 모든 것 영상을 다시 보게 되었는데, 새롭게 이해되는 부분들이 많았다. 영상에서 소개된 tensorflow코드가 VAE의 전체적인 구조를 파악하는 데 도움이 되었는데, 이를 참고하여 pytorch로 VAE를 구현해보았다. 데이터는 MNIST를 활용했다.

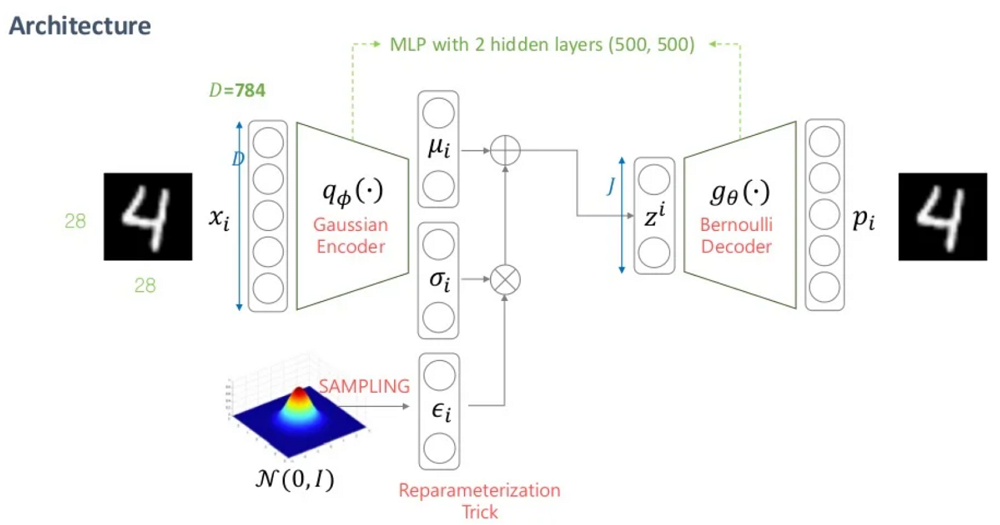
VAE의 전체적인 구조다. 출처

학습 방법은 얼핏보면 오토인코더와 유사하다. 인코더는 입력 $x$를 받아 latent vector $z$를 만들어내고, 디코더는 $z$를 입력받아 $x$를 복원시킨다.

Loss = Reconstruction_Error + KL_div

입력 x와 출력 x_reconst의 차이가 감소하도록 Reconstruction Error를 줄이는 것이 목적이면서, 추가로 KL_term도 고려한다. KL_term은 감소시킴으로써 $z$를 샘플링하는 함수를 정규분포와 유사하도록 Approximation 할 수 있다. 이 때 Variational Inference를 이용하는데, 이에 대한 개념은 이곳에 정리했다.

1. Encoder

• 입력 : (batch_size, h*w*c)
• 출력 : $\mu$와 $\sigma$ 두가지. 각각의 크기는 (batch_size, latent_dim)

class Encoder(nn.Module):
    def __init__(self, x_dim=img_size**2, h_dim=hidden_dim, z_dim=latent_dim):
        super(Encoder, self).__init__()

        # 1st hidden layer
        self.fc1 = nn.Sequential(
            nn.Linear(x_dim, h_dim),
            nn.ReLU(),
            nn.Dropout(p=0.2)
        )

        # 2nd hidden layer
        self.fc2 = nn.Sequential(
            nn.Linear(h_dim, h_dim),
            nn.ReLU(),
            nn.Dropout(p=0.2)
        )

        # output layer
        self.mu = nn.Linear(h_dim, z_dim)
        self.logvar = nn.Linear(h_dim, z_dim)

    def forward(self, x):
        x = self.fc2(self.fc1(x))

        mu = F.relu(self.mu(x))
        logvar = F.relu(self.logvar(x))

        z = reparameterization(mu, logvar)
        return z, mu, logvar

인코더는 크게 3 단계의 Linear Layer로 이뤄져 있다. 마지막 Output Layer에서 $\mu$와 $\sigma$의 네트워크를 따로 만들고 reparameterization 함수로 최종 latent vector $z$를 구한다.

def reparameterization(mu, logvar):
    std = torch.exp(logvar/2)
    eps = torch.randn_like(std)
    return mu + eps * std

Reparameterization 함수를 보면 $N(0, I)$ 분포에서 eps를 랜덤추출하고, 여기에std를 곱하고 mu를 더해 최종 $z$를 구한다. 처음부터 $N(\mu, \sigma^2I)$에서 $z$를 샘플링하지 않고 Reparameterization 하는 이유는? 역전파 알고리즘때문이다.

역전파 알고리즘은 Loss 함수의 Derivative가 네트워크 뒷단에서부터 앞단까지 전달되며 Parameter를 업데이트하는데, Parameter인 $\mu$와 $\sigma$가 $N(\mu, \sigma^2I)$ 처럼 랜덤 샘플링 과정 안에 있으면 Derivative 전달이 어렵다.
Reparameterization 함수를 통과한 $z$값은 디코더의 입력으로 전달해준다.

2. Decoder

• 입력 : (batch_size, latent_dim)
• 출력 : 베르누이 분포의 파라미터 $p$값. (batch_size, h*w*c)

class Decoder(nn.Module):
    def __init__(self, x_dim=img_size**2, h_dim=hidden_dim, z_dim=latent_dim):
        super(Decoder, self).__init__()

        # 1st hidden layer
        self.fc1 = nn.Sequential(
            nn.Linear(z_dim, h_dim),
            nn.ReLU(),
            nn.Dropout(p=0.2),
        )

        # 2nd hidden layer
        self.fc2 = nn.Sequential(
            nn.Linear(h_dim, h_dim),
            nn.ReLU(),
            nn.Dropout(p=0.2)
        )

        # output layer
        self.fc3 = nn.Linear(h_dim, x_dim)

    def forward(self, z):
        z = self.fc2(self.fc1(z))
        x_reconst = F.sigmoid(self.fc3(z))
        return x_reconst

인코더와 대칭적으로 디코더도 3 단계의 Linear Layer로 이뤄져 있다.

학습 데이터가 MNIST이고, 이미지 데이터에선 Generator(디코더)를 베르누이 분포로 가정하므로 디코더의 출력은 $p$(베르누이 분포의 파라미터)이다. $p$값의 범위는 0에서 1 사이이므로 마지막 Acitivation 함수는 Sigmoid 함수로 세팅했다.

만약 디코더의 분포를 정규분포로 가정한다면? 디코더의 출력은 정규분포의 파라미터인 $\mu$와 $\sigma$가 될 것이고 마지막 Layer의 Activation도 Relu로 구현했을 것이다.

3. Train

for epoch in range(n_epochs):
    for i, (x, _) in enumerate(train_dataloader):
        # forward
        x = x.view(-1, img_size**2)
        x = x.to(device)
        z, mu, logvar = encoder(x)
        x_reconst = decoder(z)

        # compute reconstruction loss and KL divergence
        reconst_loss = F.binary_cross_entropy(x_reconst, x, reduction='sum')
        kl_div = 0.5 * torch.sum(mu.pow(2) + logvar.exp() - logvar - 1)

        # backprop and optimize
        loss = reconst_loss + kl_div
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

최종 목적 함수는 reconst_loss와 kl_div의 합으로 계산한다. $p(x), p_\theta(z|x), q_\phi(z|x)$ 의 관계식으로부터 목적함수를 구할 수 있다. 이 과정은 이곳에서 설명한다.

reconst_loss

$-E_{q_\phi(z|x)}{[log{p_\theta(x|g_\theta(z))}]}$

• 입력 데이터 x와 복원된 x_reconst가 유사한지 측정한다.
• $p_\theta(x|z)$가 베르누이 분포를 따른다고 가정하면 reconst_loss는 cross entropy식과 같고, 정규분포를 따른다고 가정하면 reconst_loss는 MSE식과 같다.
• 이미지 도메인에선 주로 베르누이 분포로 가정하기 때문에 구현할 때는 x와 x_reconst의 cross entropy를 구한다.
• reconst loss $= \sum_{j=1}^{D}x_jlog(p_j)+(1-x_j)log(1-p_j)$ , (D = h*w*c )

kl_div

$KL(q_\phi(z|x)||p(z))$

• $q_\phi(z|x) \sim N(\mu, \sigma^2I)$, $p(z) \sim N(0, I)$를 가정
• 여기서 $\mu$와 $\sigma$는 인코더의 출력값
• 정규분포 사이의 kl_div를 구하는 적분식은 closed form으로 다음과 같이 구할 수 있다.
• kl loss $= 0.5*\sum_i^J{(\mu_{j}^2+\sigma_{j}^2 - log(\sigma_{j}^2) - 1)}$, (J는 latent space, z의 차원)

4. Test 데이터, Reconstruction 결과

전체 코드는 다음과 같다. (colab link)

학습 과정에서 사용하지 않은 Test 데이터로 성능을 확인해보았다. 홀수 번째 Column이 원데이터이고, 짝수 번째 Column이 왼쪽 데이터에 대한 Reconstruction 결과다. MNIST 데이터는 사람 얼굴처럼 복잡한 분포를 가지고 있지 않다보니 대부분의 Test 데이터에서 Reconstruction 성능이 좋았다.

다만 생성 결과가 Blur한 특징을 있는데, 이는 여러가지 해석이 있다. 그 중 하나로 GAN과 VAE의 차이점을 비교한 해석을 소개하면

• GAN도 생성모델이지만 blur한 현상은 잘 나타나지 않는다. GAN은 Discriminator에 이미지 전체가 입력되고, 이 이미지가 진짜인지 가짜인지 즉 0또는 1의 값이 출력되는 반면,
• VAE의 최종 목적 함수의 일부인 reconstruction loss를 살펴보면
  $\sum_{j=1}^{D}x_jlog(p_j)+(1-x_j)log(1-p_j)$
• 픽셀마다 $x_jlog(p_j)+(1-x_j)log(1-p_j)$ 를 계산하여 모두 더한다.
• 이때문에 VAE는 픽셀별 error값을 평균적으로 줄이는 방향으로 학습이 되는 것이다. 그래서 VAE의 생성 결과가 blur할 것이란 해석이다.
• 이와 달리 GAN은 이미지 전체를 보고 진짜 이미지라고 판별되도록 학습되는 Adversarial Loss를 쓴다.
• VAE와 구조는 비슷하지만 Adversarial Loss 쓰는 AAE(Adversarial Auto-Encoder)도 있다. 일반적으로 VAE보다 AAE가 생성 성능이 좋다고 알려져있다.

다음 글에서는 VAE를 공부하며 어려웠던 질문들에 대해 정리해보고 논문에 나오는 용어와 전체적인 개념을 정리해봐야겠다.

5. Reference

https://youtu.be/o_peo6U7IRM