VAE(Varitional Auto-Encoder)를 알아보자
VAE는 Generative Model이지만 AE(Auto-Encoder)는 Generative Model이 아니다. Latent Space()로부터 새로운 데이터 를 생성하고 싶을 때, VAE는 Prior dist에서 값을 샘플링하면 되지만, AE는 값을 샘플링할 방법이 없다. 이번 글에서는 VAE 개념과 용어를 정리해보겠다.
논문 : Variational Autoencoder(VAE) (Kingma et al. 2014) https://arxiv.org/abs/1312.6114
참고한 자료 : 이활석님의 <오토인코더의 모든것> https://youtu.be/rNh2CrTFpm4
목차 Summary
이 글은 VAE가 왜 생성모델인지, Variational Inference는 무엇인지에 대한 글입니다. 아래 목차를 클릭하시면 해당 제목으로 이동하실 수 있습니다.
- VAE와 AE는 뭐가 다른 건가?
1.1. 그런데 Manifold는 늘 존재할까?
1.2 그럼 Latent Variable z는 어떻게 찾을까? : Variational Inference - 사이의 관계?
2.1 KL divergence란? - Optimization 문제 정리
- VAE의 목적 함수 (loss 함수)
4.1 가정 세 가지
4.2 Reparameterization Trick
1. VAE와 AE는 뭐가 다른 건가?
VAE(Variational AutoEncoder)와 AE(AutoEncoder)는 둘 다 오토인코더 구조이다.
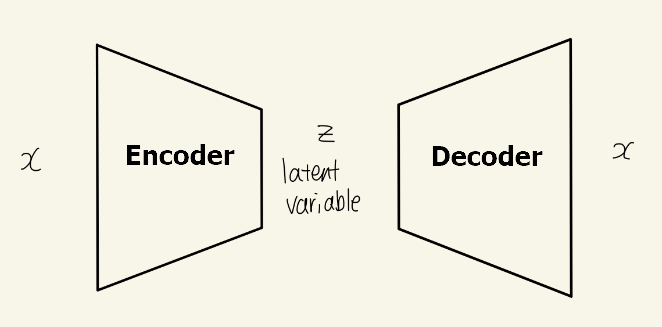
오토인코더 구조란 입력 변수()가 Encoder를 거쳐 Latent Variable인 에 매핑되고, 이 가 Decoder를 거쳐 가 출력되도록 학습되는 형태다. (target이 ) AE와 VAE 모두 오토인코더 구조지만 두 모델의 목적이 다르다. AE는 앞단인 Encoder를 찾는 것이 목적이지만, VAE는 뒷단의 Decoder 네트워크를 학습하는 것이 목적이다.
-
AE의 목적 : 학습 데이터가 있을 때, 중요 Feature들로 압축된 Manifold를 찾는 것. (=이렇게 압축하는 Encoder를 찾는 것.) 학습 데이터 와 유사한 새로운 데이터를 생성할 수 없다.
-
VAE의 목적 : 학습 데이터에 있는 데이터 포인트를 라고 할 때, 에 대해 Likelihood를 최대화하는 을 구하는 것이 목적이다. 의 분포를 알면, 를 샘플링하여 우리가 원하는 분포, 즉 학습 데이터 와 유사한 새로운 데이터를 생성할 수 있다. (Generative Model)
여기서 Manifold 라는 개념이 등장한다. Manifold는 '차원 축소된 어떤 공간'이다. 데이터가 잘 압축되었다는 것은, 학습 데이터가 공통으로 가지는 핵심 Feature들을 잘 찾았다는 의미와 같다. (그 Feature가 무엇인지는 알 수 없다. - Unsupervised Learning이기 때문에)
예를 들면, 이미지 데이터같이 차원이 큰 학습데이터를 다룰 때, 이보다 더 낮은 차원의 서브 스페이스(Latent Space)로 매핑이 가능할 것이라 가정하는 것이다.
1.1. 그런데 Manifold는 늘 존재할까?
압축이 제대로 안 될 수도 있지 않나? 학습 데이터마다 다르겠지만 특정 도메인의 이미지 데이터(ex. 사람 얼굴 이미지로 이루어진 학습 데이터) 의 경우 Manifold가 존재한다. 만약 차원 (channel, h, w) = (3, 28, 28) 짜리 데이터 값을 랜덤하게 추출했다고 하자. 예를 들어 N(0, 1)에서 픽셀 값을 랜덤추출하는 것이다. 이를 시각화하면 대부분 아래와 같이 슈팅스타(?)같은 이미지가 생성된다. 사람 얼굴 이미지, 고양이 이미지,.. 등 우리가 흔히 이미지라고 인식하는 데이터는 (channel, h, w) 차원 상에 골고루 관측치가 존재하는 게 아니라, 특정 Manifold에 모여있는 것이다.

1.2 그럼 Latent Variable 는 어떻게 찾을까? : Variational Inference
VAE의 목표
- 다루기 쉬운 분포로부터 를 샘플링해서,
- 를 적절한 Decoder를 통과시켜 를 Generate하는 것
벡터는 Manifold 좌표다. VAE 학습이 제대로 됐다면, 값에 조금씩 변화를 줬을 때 Generated된 이미지에서도 유의미한 변화가 있어야 한다.
이때 를 그냥 (=prior 분포) 에서 샘플링하는 대신, 이상적인 확률 분포 (=Posterior dist)에서 샘플링하고자 한다. (최종적으로 학습 데이터 의 분포와 최대한 가까운 데이터를 생성하기 위해서다.)
문제는 그 이상적인 확률 분포 를 모르기 때문에 추정해야 한다. 이 확률 분포를 추정하기 위해 Variational Inference를 이용한다. Variational Inference는 우리가 알고 있는 확률 분포 중 하나로 를 가정하고 이 분포의 파라미터 를 바꿔가며 이상적인 확률 분포에 Approximation 하는 방법이다. (는 정규분포로 가정한다. 그 이유는 이후 4.1 가정 세 가지에서 설명한다.) 파라미터가 , 두 가지가 있으니 Optimization 식도 두 가지다.
이 문제를 풀기 위해 사이의 관계식을 이용한다.
Q. Manifold는 굉장히 복잡(complex)할 것 같은데 를 정규분포에서 샘플링해도 충분할까?
A. Decoder가 Neural Net이기 때문에, 실제로 학습해야 할 Manifold가 복잡하더라도 앞에 1~2 개 레이어가 그 Manifold 찾는 역할을 수행한다.
2. 사이의 관계?
사이의 관계식으로 VAE의 최종적인 목적함수를 도출한다.
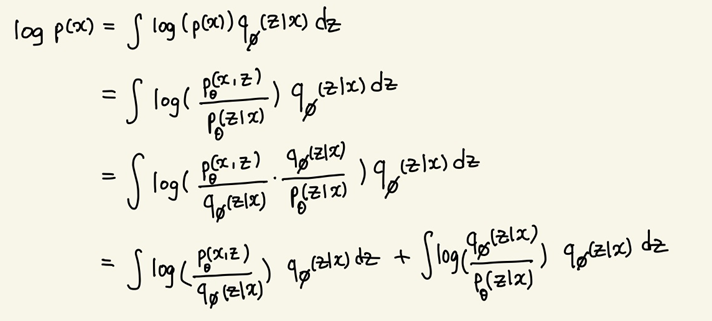
관계식을 도출하는 전체적인 과정은 위와 같다. 한 줄씩 살펴보면,
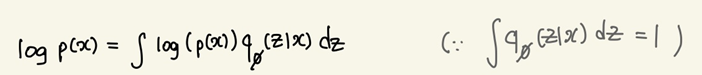
는 확률밀도함수이므로 위와 같은 식이 성립한다.
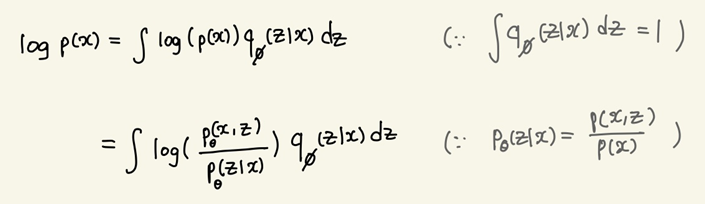
조건부 확률 정의에 의해 위와 같이 변형할 수 있다.
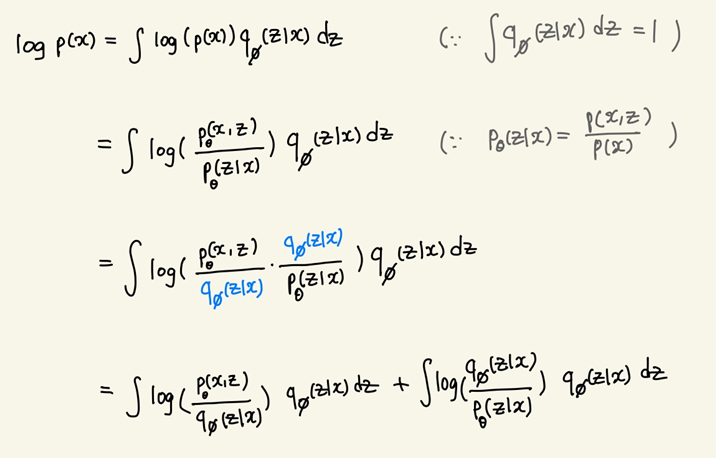
여기에 를 도입하여 식을 쪼갠다. 내부의 곱 연산이 합 연산으로 분리된다.
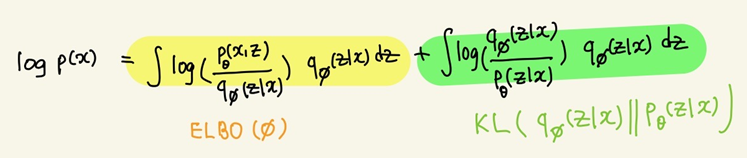
최종적으로, 학습 데이터의 분포 는 ELBO term과 KL term으로 쪼개진다. (ELBO : Evidence Lower Bound)
Q. Evidence?
, (베이즈 정리)
- : 관측치, : 파라미터
- : 사후확률(Posterior) 데이터를 관찰한 이후에, 이 파라미터가 성립할 확률
- : 사전확률(Prior) 데이터 관찰 이전에, 이 파라미터가 성립할 확률
- : Evidence, 데이터 전체의 분포
- : Likelihood, 주어진 파라미터에서 이 데이터가 관찰될 확률
2.1 KL divergence란?
데이터 공간에 두 개의 확률분포 , 가 있을 경우, 유사성을 측정하기 위해 두 확률분포 사이의 거리를 계산하는 방법 중 하나다.
두 분포가 동일한 경우(=확률밀도함수가 동일할 경우) KL divergence는 0이다. 그리고 KL divergence 값은 항상 0보다 크거나 같다.
다시 VAE로 돌아와서, Variational Inference의 목적은 이 KL term을 최소화하는 것이다. 다시 말해, 이상적인 분포 에 가 근사하길 바란다. 그런데 분포를 모른다고 했는데 어떻게 KL term을 계산할까?

좌변의 는 학습 데이터 의 분포를 나타낸다. 학습 데이터가 어떠한 분포를 따르는지 알 수는 없지만, 일단 Train Set으로 주어진 상태이므로 는 어떠한 상수값이라고 가정한다. 따라서 KL term을 최소화하는 문제는 ELBO term 을 최대화하는 문제와 같다. 식으로 표현하면 다음과 같다.

이므로, 를 만족한다.
ELBO term을 변형하여 다음과 같이 분리할 수 있다.
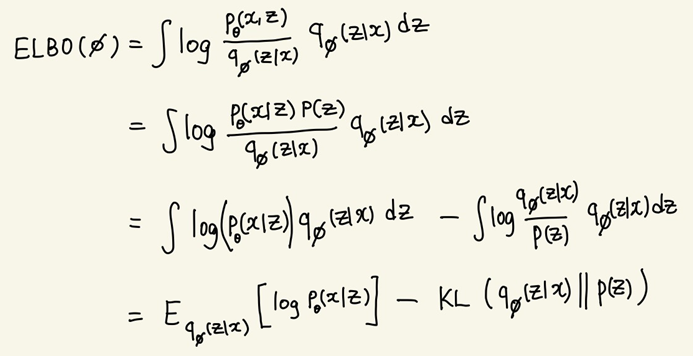
3. Optimization 문제 정리
지금까지의 관계식을 정리하면,
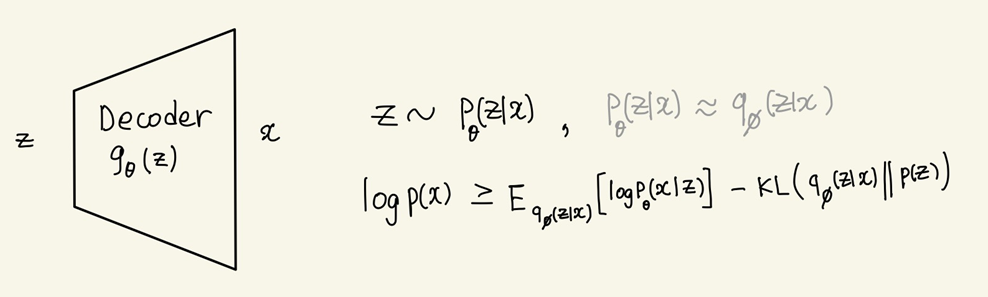
VAE에서 Optimization 문제는 총 2가지다.
Optimization 문제 1 : (Variational Inference)
Optimization 문제 2 : (MLE)
Q. MLE ?
네트워크 출력값(=) 이 있을 때, 우리가 원하는 정답 (=)가 나올 likelihood가 높기를 바람.
4. VAE의 목적 함수 (loss 함수)
두 Optimization 문제를 모두 풀 수 있는 최종 목적 함수는 다음과 같다. (Total Loss는 각 샘플()별 Loss의 합과 같다.)
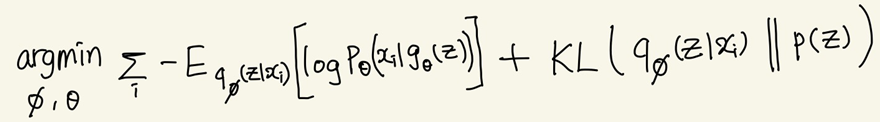
4.1 가정 세 가지
VAE 가정
가정 1:
가정 2:
가정 3:
최종 목적 함수를 Reconstruction Error와 Regularization으로 나눌 수 있다.
1) Reconstruction Error
에서 샘플링한 에 대해 log likelihood를 최대화하는 것이 목표다. 이 부분은 오토인코더의 Reconstruction Error와 동일하다. Reconstruction Error는 입력과 출력이 유사한 분포를 가지는지 측정한다. 의 분포를 베르누이로 가정하면 Cross Entropy이고, 정규분포로 가정하면 MSE이다. 예를 들어 MNIST와 같이 이미지 도메인의 경우 를 베르누이 분포로 가정한다. 따라서 이 경우 Reconstruction Error는 Cross Entropy와 같다.
다음은 Reconstruction Error가 계산되는 과정이다.
적분값을 구하기 쉽지 않으므로 몬테카를로 샘플링을 이용한다. 몬테카를로 샘플링은 확률 분포를 모르더라도 샘플링으로 기댓값을 구할 수 있는 방법이다. 분포에 상관없이 독립추출만 보장되면, 대수의 법칙에 의해 샘플링 평균값이 기댓값에 수렴한다.
-
에서 총 L개의 를 샘플링한다.
-
target 에 대해 log likelihood를 계산한다.
-
이를 평균낸다.
편의상 L=1로 잡는다. 따라서
로 계산할 수 있다.
2) Regularization
1)번 문제에서 Reconstruction Error를 작게 만드는 를 여러 후보 찾았다면, 그 중 Prior dist인 와 유사한 분포를 선택한다. 는 새로운 이미지()를 생성할 수 있는 컨트롤러로서, 다루기 쉬운 분포로 가정한다.
을 정규분포로 가정 <가정 3> 한 이유는, 정규분포끼리는 KL term을 계산하기 쉽기 때문이다.
- 가정 2:
- 가정 3:
(J는 latent space, z의 차원)
Q. 논문에서 자주 등장하는 용어 'intractable posterior distribution'에서 "intractable"의 의미가 무엇일까.
A. 적분식이 closed form 이 아닌 경우 intractable 하다고 표현한다.
VAE에서 를 정규분포로 가정한 이유는, KL div를 계산하는 적분식이 closed form이 되어야 하기 때문이다. (참고링크) 역전파 알고리즘으로 학습하기 위해선 Loss가 미분가능 해야 한다. 그런데 KL div는 식 자체로 적분이 들어가 있고, 그 적분을 closed form으로 풀 수 없으면 미분 계산이 불가능하다. KL div는 정규분포를 제외하곤 미분가능한 경우가 많지 않다.
를 샘플링하는 분포를 원하는 모양으로 세팅하지 못하고 정규분포로만 가정해야한다는 점은 VAE의 한계이기도 하다. 예를 들어, 여러 개의 봉우리가 있는 Gaussian Mixture같은 임의의 분포를 분포로 세팅할 수 없다. (반면, AAE는 Adversarial Loss를 이용하기 때문에 정규분포뿐만 아니라 임의의 Prior dist로 매칭 가능하다.)
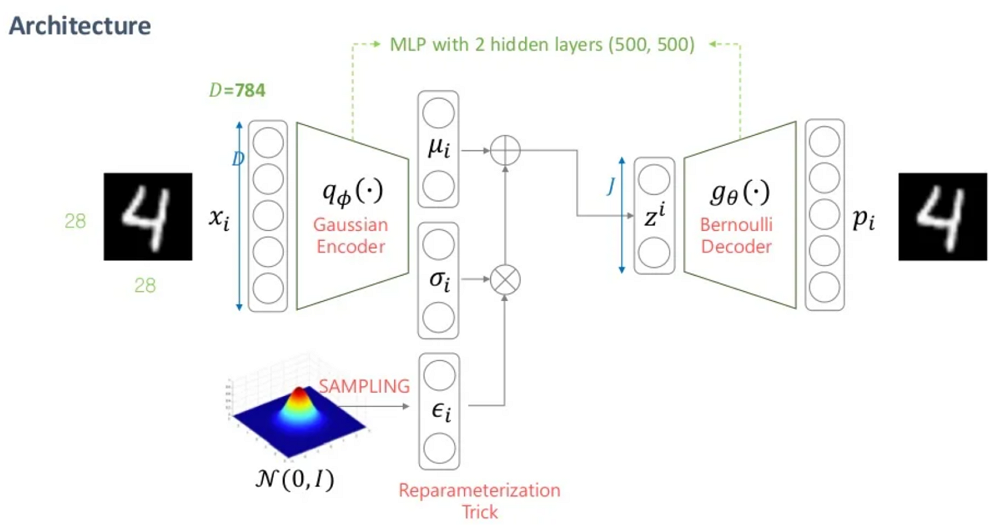
VAE의 전체 구조는 아래와 같다.
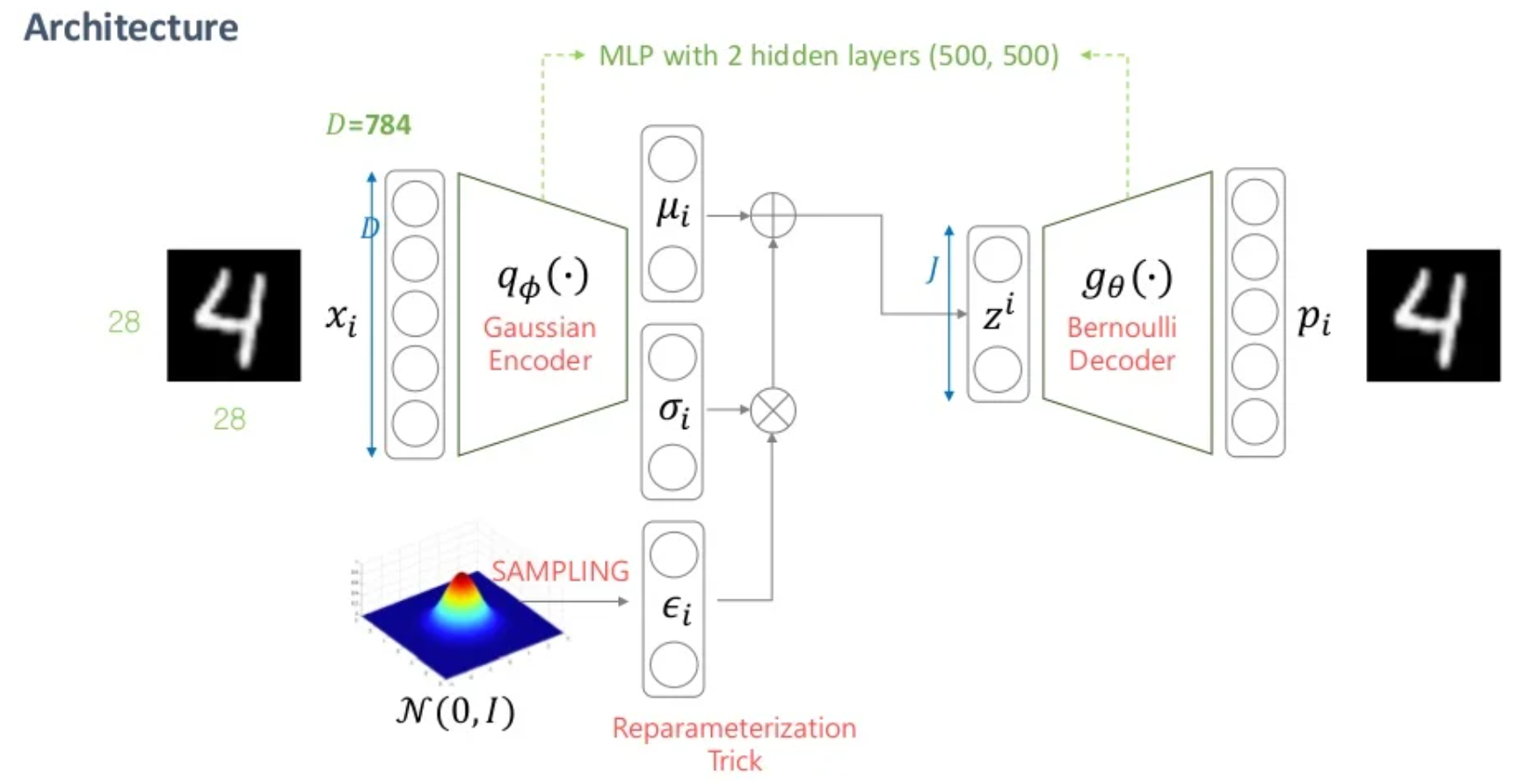
4.2 Reparameterization Trick
"가정 3: " 에서 를 직접 샘플링하지 않고, 를 샘플링하여 위와 같은 Reparameterization Trick을 쓰는 이유는 Backward Propagation(역전파 알고리즘)으로 와 를 업데이트하기 위함이다.
- 역전파 알고리즘은 최종 목적 함수의 Gradient 값이 네트워크 뒷단에서부터 앞단까지 전달되어 파라미터가 업데이트된다. 그런데, 이 파라미터가 랜덤샘플링안에 섞여 있으면 Gradient 전달이 불가능하다.
마무리하며
VAE의 개념과 논문에 등장하는 용어들을 정리해봤다. VAE는 이미지 도메인뿐만 아니라 시계열 데이터에서도 적용할 수 있다고 하니, Anomaly Detection을 공부할 때 적용해봐야겠다.
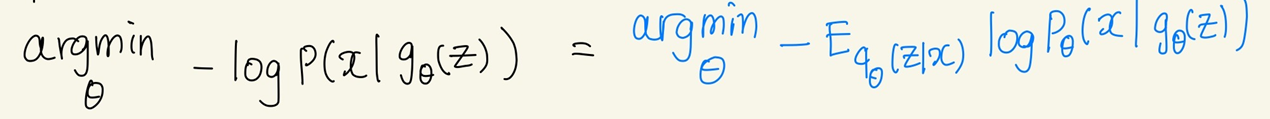

정말 많은 도움이 되었습니다. 감사합니다.