CS224W 3.3 Embedding Entire Graphs

1.개요

1.1. 목표

• 서브그래프나, 전체 그래프 $G$를 embedding space에 매핑 : $\mathbf{z}_G$

1.2. 응용

• 분자구조에서 독성/무독성 여부를 분류하는 작업
• 이상 그래프를 탐지하는 작업 (Anomaly Detection)

2. Survey

2.1. Approach 1: naive approach

• Idea
  • (서브)그래프 $G$에 대하여, 일반적인 그래프 임베딩 기법을 사용
  • (서브)그래프 $G$에 있는 각각의 노드임베딩의 단순합(혹은 단순평균)을 사용

    $\mathbf{Z}_G=\displaystyle\sum_{v\in G} \mathbf{Z}_v$

  • Duvenaud et al., 2016 : 그래프 구조 기반 분자를 분류하는 데에 사용됨

2.2. Approach 2: virtual node

• Idea
  • (서브)그래프를 나타낼 수 있는 "virtual node" 개념을 도입
  • Li et al., 2016 : 서브그래프 임베딩을 위한 기법으로 제안
  • 💡virtual node를 선정하는 방법? [Todo] 논문:Gated Graph Sequence Neural Networks, ICLR 2016.

2.3. Approach 3: anonymous walks

2.3.1. Idea

• "익명걷기(anonymous walks)" : 노드를 모른채로 걷는다 (패턴만 파악)
  • 랜덤워크에서 처음 방문했을 때의 인덱스로 random walk를 정의
  • (i) $A\rightarrow B\rightarrow C\rightarrow B\rightarrow C$
  • (ii) $C\rightarrow D\rightarrow B\rightarrow D\rightarrow B$
  • 위 (i)와 (ii)는 $1\rightarrow 2\rightarrow 3\rightarrow 2\rightarrow 3$과 같은 동일한 랜덤워크로 정의됨
  • 노드에 익명성을 부여하므로 개별노드를 식별할 수 없음. Agnostic
• Number of Walks Grows
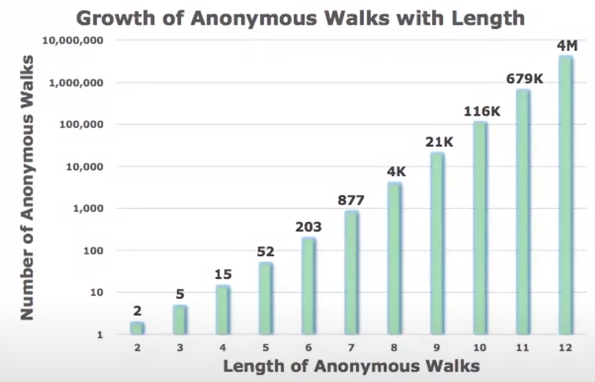
  • 걸음종류의 개수가 어떻게 랜덤워크의 길이에 따라 어떻게 증가하는가?
  • 길이가 3인 anonymous walk 종류의 개수는 몇개일까?

    $w_1 = 111,w_2=112,w_3=121,w_4=122,w_5=123$
    💡길이가 3인 anonymous walk의 개수는 5개
    💡길이가 5인 anonymous walk의 개수는 52개 .....
    💡길이가 12인 anonymous walk의 개수는 4,000,000개 .....

  • 위와 같이 # of anonymous walks 의 개수는 길이에 따라 지수적으로 증가함

    

2.3.2. Simple use of anonymous walks

• approach
  • 길이가 $l$인 anonymous walks 를 수행(2.3.3.)하고, 익명걷기 $w_i$ 각각의 count를 기록
  • 이에 대한 각각의 count를 확률분포로 나타내어, 그래프의 표현으로 사용
• 예제
  • $l=3$
  • 그래프를 $5-dim$ vector로 표현할 수 있음
    • $l$이 3인 anonymous walks $w_i$는 $111, 112, 121, 122, 123$으로 총 5개이기 때문
  • $\mathbf{Z}_G[i]=w_i$의 확률

2.3.3. Sampling Anonymous Walks (AW)

• Sampling AW : $m$ RW set을 독립적으로 생성
• 이 때 $m$(얼마나 많은 랜덤워크를 수행해야할까?)의 값을 어떻게 선정할까?
  • 빈도 & 발생확률에 대한 추정이 정확하도록 샘플링할 필요가 있음
    • $\epsilon$보다는 크고, $\delta$보다는 작은 오류를 갖는 확률 분포를 원함
  • 수학적으로 아래의 공식에 의거하여 $m$을 결정할 수 있음

    $m=\displaystyle\left[\frac{2}{\epsilon ^2}(log(2^\eta - 2) - log(\delta)) \right]$
    💡 $eta$는 길이 $l$인 AW의 총 개수
    💡 $l=7이면 \eta=877$이며, $\epsilon = 0.1, \delta=0.01$로 세팅하면,
    💡 $m=122,500$개의 AW를 샘플링한다!

2.3.4. Learn Walk Embeddings

• 단순히 각 AW를 표현하는 것 대신, AW $w_i$의 임베딩 $\mathbf{z}_i$를 학습해보자!

• 이 때, AW의 임베딩 $\mathbf{z}_i$ 뿐만 아니라, 그래프 임베딩 $\mathbf{Z}_G$도 학습

  • $Z=\{z_i:i=1\ldots \eta\}$, $\eta$는 샘플링한 AW의 수

• 어떻게 walks를 임베딩할까?

  • Idea : walks를 입력하면, 이와 유사한 walk를 예측
    💡Deepwalk, node2vec과 유사한 컨셉

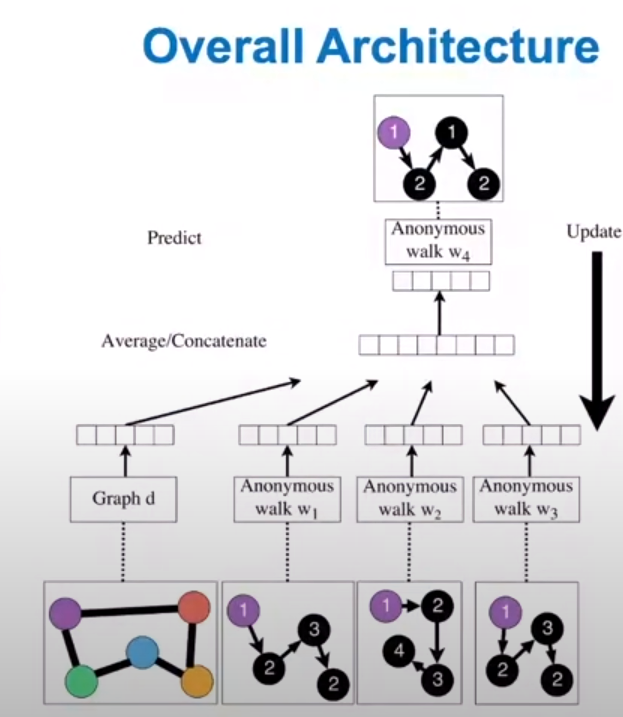
• Approach :

  • Notation ; $\mathbf{Z}_G$ : 학습될 전체 그래프의 임베딩 벡터

  • (i) node 1에서 시작하여 랜덤워크를 수행

    • 즉, 노드 $u$로 부터 출발한 길이 $l$인 $T$개의 서로 다른 RW를 수행

      $N_R(u)= \{w_1^u , w_2^u,\ldots,w_T^u \}$

      • 노드 $u$의 이웃 : 서로 다른 RW

  • (ii) $\Delta$-size(윈도우)의 동시발생하는 walks를 예측하기 위해 학습

    • 예: $\Delta =1$이고, $w_1,w_3$이 주어질 때, $w_2$를 예측

  • Objective function

    $\displaystyle \max_{Z,d}\displaystyle\sum_{t=\Delta}^{T-\Delta} logP(w_t|w_{t-\Delta},\ldots,w_{t+\Delta},\mathbf{Z}_G)$

    • 예시 기준: $w_t$는 노드 1에서 시작되는 AW
    • $T$의 의미는? RW를 수행하는 횟수
    • 💡기본적으로는 MLE(최대우도법)에 의해 최적화
    • $\Delta$개만큼의 AW($=\mathbf{Z}_G$)를 예측하는 것

  • Objective function 구성요소에 대한 detail

    $P(w_t|\{ w_{t-\Delta}, \ldots, w_{t+\Delta}, \mathbf{Z}_G\})=\displaystyle\frac{ exp(y(w_t))}{\sum_{i=1}^{\eta} exp(y(w_i))}$

    • 분모는 모든 가능한 Walks (이때, 노드 임베딩에서와 마찬가지로 negative sampling을 활용함

    $y(w_t)=b + U \cdot(cat(\frac{1}{2\Delta}\sum_{i=-\Delta}^{\Delta} \mathbf{z}_i, \mathbf{Z}_G))$

    • $\Delta$만큼의 AW임베딩 평균을 $\mathbf{Z}_G$에 concat
    • $b\in\mathbb{R}$와 $U\in\mathbb{R^D}$는 학습 파라미터로, 선형 레이어를 의미

    • Reference Anonymous Walk Embedding, ICML 2018.

  • (iii) 최적화 이후 그래프 임베딩 $\mathbf{Z}_G$를 얻음

  • (iv) 그래프 임베딩 $\mathbf{Z}_G$를 이용하여 그래프 분류작업과 같은 예측수행

    • Option 1 : 내적을 활용하는 방법 $\mathbf{Z}_{G_1}^{T}\mathbf{Z}_{G_2}$
    • Option 2 : neural network를 활용
      :: $\mathbf{Z}_G$를 입력으로, 입력그래프의 레이블을 예측하는 신경망에 사용

3. Summary

• 그래프 임베딩에 대한 3가지 방법론
  • Approach 1 : 노드를 임베딩하고 이를 합계/평균내어 그래프임베딩
  • Approach 2 : (서브)그래프를 대표하는 슈퍼노드를 생성하고, 이 노드를 임베딩하는 방법
  • Approach 3 : Anonymous Walk 임베딩
    • (1) AW를 샘플링하여, 각 AW의 발생횟수 그래프 임베딩
    • (2) AW를 임베딩하고, 각 임베딩을 concat하여 그래프 임베딩

4. Preview

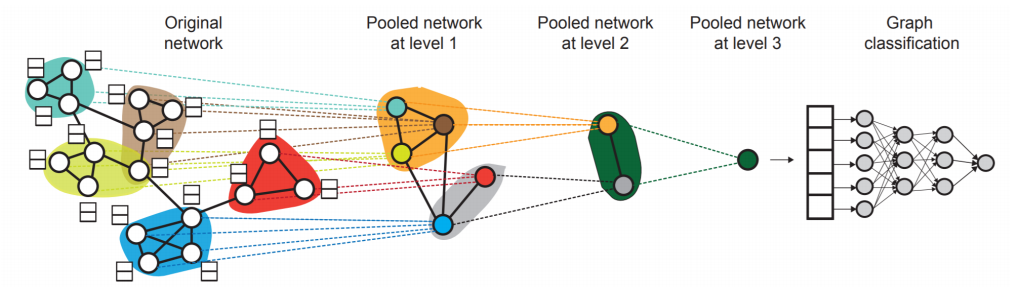
• Hierarchical Embeddings
  • Lecture 8.에서 graph embedding에 대한 발전된 방법에 대해 다룰 예정
  • 계층적으로 노드를 클러스터링하고, 각 클러스터에 따라 노드 임베딩을 sum/avg하는 등 집계하는 방식을 다루게 될 것. (Latent, CNN)

5. 임베딩의 활용

5.1. 노드 임베딩의 활용

• Clustering/Community detection
  • Embedding space에 사상된 각 포인트들을 클러스터링
• Node Classification
  • 임베딩 벡터 $\mathbf{z}_i$를 이용하여, node $i$의 레이블을 예측
• Link prediction
  • 임베딩 벡터$(\mathbf{z}_i, \mathbf{z}_j)$ 기반으로 edge $(i,j)$를 예측
  • 노드 임베딩을 결합$(\mathbf{z}_i, \mathbf{z}_j)$할 때 다음 방법들을 활용

    Concatenate: $f(\mathbf{z}_i, \mathbf{z}_j)=g([\mathbf{z}_i, \mathbf{z}_j])$ 유향그래프에 적합, [i,j][j,i]가 다른확률출력
    Hadamard: $f(\mathbf{z}_i, \mathbf{z}_j)=g(\mathbf{z}_i* \mathbf{z}_j)$ 무방향그래프에 적합, A*B=B*A
    Sum/Avg: $f(\mathbf{z}_i, \mathbf{z}_j)=g(\mathbf{z}_i+ \mathbf{z}_j)$
    Distance: $f(\mathbf{z}_i, \mathbf{z}_j)=g(||\mathbf{z}_i- \mathbf{z}_j||_2)$

• Graph classification
  • node 임베딩의 집계 방식이나, AW 방식을 통해 취득한 그래프 임베딩 $\mathbf{Z}_G$를 기반으로 (서브)그래프의 레이블을 예측하는 방식

6. Lecture part 3 총정리

• graph representation learning에 대한 논의 (without feature engineering)
  • Encoder-decoder framework
    • Encoder : 임베딩 룩업
    • Decoder : 노드 유사도에 매칭되는 임베딩 기반으로 스코어 예측
  • Node similarity Measure : (biased) random walk
    • DeepWalk, Node2Vec
  • Graph embedding으로의 확장
    • 노드 임베딩 집계방식 / AW(익명걷기..) 임베딩