CS224W 4.1 Graph as Matrix: Page Rank, Random Walks and Embeddings

1. 개요

• graph를 matrix 관점으로 학습하고 분석하는 방법에 대해 알아보기

1.1. Example: 그래프로 표현되는 웹

• Web as a graph:
  • 노드: 웹 페이지
  • 에지: 하이퍼링크들
• Side issue: What is nodes?
  • 동적으로 생성되는 웹페이지들
  • dark web - 탐색으로는 접근 불가능한..

⚠ 오늘날의 웹페이지의 '하이퍼링크'는 transaction(좋아요, 포스트, 구매 등)에 초점이 맞추어져 있으나, 4강의 강의에서 다루는 내용은 '페이지에서 페이지로 이동'에 초점을 맞춤

1.2. 네트워크의 다른 사례들

• Citation network: 노드(논문), 에지(인용)
• References in an Encyclopedia: 노드(개념), 에지(연관개념 페이지)

1.3. 아이디어와 목표; Ranking Nodes on the Graph

• 웹 검색의 관점에서, 어떤 노드가 중요한지 판단하는 것이 중요
• 모든 페이지들은 동등하게 중요하지 않음
  • 잘 알려진 페이지(stanford.edu)와 알려지지않은 페이지(ekfsmdkfoe.com)의 중요성은 서로 다를것
• 웹그래프의 링크 구조에서 페이지(노드)의 중요도를 어떻게 매길것인가?
  • 어떤 페이지가 더 중요하고, 더 대중적이며, 더 신뢰할만한지 등등..
  • 목표 웹 검색의 결과로 어느 페이지를 상단에 위치시킬 것인가?

1.4. Link Analysis Algorithms

• 노드 중요도를 링크 분석을 통해 판별하는 여러 접근방식
  • PageRank
  • Personalized PageRank(PPR)
  • Random Walk with Restarts

2. PageRank (Google algorithm)

2.1. Idea

• 웹페이지 중요성을 계산하기 위한 Idea: Links as votes (링크를 투표로 생각하기!)
  • 많은 링크를 가진 페이지는 더욱 중요하다
    • In-coming links(조작이어려움)? Out-going links(조작이쉬움)?
  • In-links를 투표로 생각해보면?
    • stanford.edu : 23,400개의 in-links
    • ekfsmdkfoe.com : 1개의 in-links
• 모든 in-links는 동일할까?
  • 직관적으로, 중요한 페이지가 링크한 페이지가 더 중요할 것
  • 이 직관으로부터, 이 문제는 Recursive problem으로 생각할 수 있음
    • 내가 받는 투표의 양은, 투표한 사람의 중요성에 달려있음
    • 그 사람이 받는 투표의 양은, 그 사람에게 투표한 사람의 중요성에 달려있음..

2.2. The "Flow" Model

2.2.1. 예시

• 중요한 페이지로부터의 "투표(in-links)"는 더 중요함
  • 각 링크의 투표는 소스페이지의 중요성에 비례
    • 중요도가 $r_i$인 페이지 $i$가 $d_i$개의 out-links를 가지고 있다 가정
    • 각 링크는 $r_i / d_i$ 만큼의 투표를 의미: 중요도를 out-links 수만큼 균등분할
      • 나의 중요도를 내가 연결한 다른 페이지에 균등하게 분할!

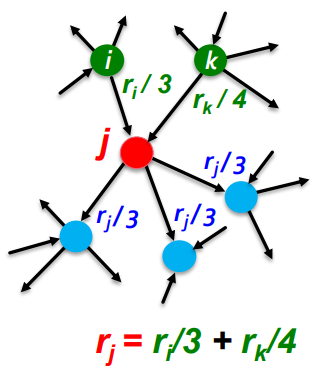
2.2.2. "rank"의 정의

• node $j$의 순위 $r_j$를 아래와 같이 정의

  $r_j=\displaystyle\sum_{i\rightarrow j}\frac{r_i}{d_i}$

  • $d_i \ldots$ 노드 $i$의 out-degree
  • $j$를 가리키는 노드 $i$의 중요성 합계/$i$노드의 차수 로 정의

• 예시: 3개의 웹페이지에서의 "Flow" equations

$r_y = r_y / 2 + r_a / 2$
$r_a = r_y / 2 + r_m$
$r_m = r_a / 2$

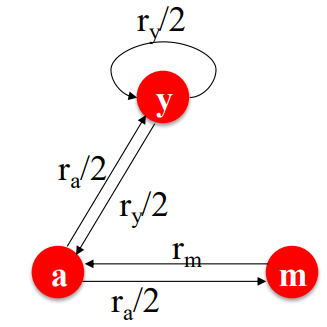
• 3개의 방정식과 3개의 미지수: 연립방정식(확장성X), 더 우아하게 해결해봅시다

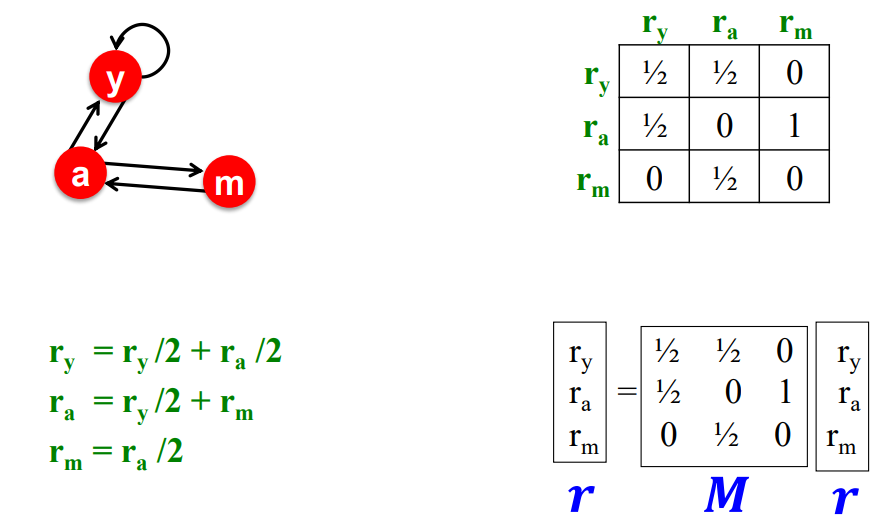
2.2.3. Matrix Formulation

• Notions

  • Stochastic adjacency matrix $M$ (not adj-list) : n by n

    • $d_j$개의 out-links를 가진 page $j$를 가정
    • $M_{ij}=\frac{1}{d_j}$, $M$은 열 확률론적 행렬(각 column의 합 = 1)
    • 이 Matrix는 이웃노드에 대한 확률 분포를 나타낸다고도 말할 수 있음!

  • Rank vector $r$: 페이지당 하나의 항목을 갖는 순위 벡터

    • $r_i$는 page $i$의 중요도 점수 (길이 n인 벡터로 표현)
    • $\sum_{i}r_i=1$

  • 위 정의에 따라, 어떤 페이지의 중요도는 간단한 행렬곱으로 표현될 수 있음

    $r_j = \displaystyle\sum_{i\rightarrow j}\frac{r_i}{d_i}$ 👉👉👉 $r = M \cdot r$

  • 어떻게 동치가 되는가?

• Intuition Connection to random walk
  • 웹에서 임의로 웹서핑을 하는 가상의 사례를 떠올려 보자.
    • time $t$, surfer는 어떤 페이지 $i$에 접속함
    • time $t+1$, surfer는 무작위로(균일한 확률로) out-links를 클릭
    • surfer는 페이지 $j$에 도달
    • 이 과정을 무한히 반복
  • 정의
    • $p(t)$의 $i$번째 좌표: 시간$t$에 surfer가 page $i$에 있을 확률
    • 이는 $p(t)$ 벡터가, 각 페이지에 대한 확률 분포를 의미함
• Objective time $t+1$에 surfer는 어느 페이지에 있는가?
  • surfer는 무작위로 랜덤하게 링크를 따라감

    $p(t+1)=M\cdot p(t)$

    • $j$로 들어오는 in-links가 $i_1, i_2, i_3$이라할 때, (2.2.3)의 Matrix formulation에서 다룬 행렬 $M$에 페이지에 대한 확률분포 $p$를 행렬곱하여 다음 시간에 위치할 확률 분포를 꼐산할 수 있음

  • surfer는 너무 오랜시간 돌아다니기 때문에 시간 $t$는 그다지 중요하지 않음
  • surfer가 무한히 돌아다니는 상황을 가정할 때, 다음을 유도할 수 있음

    $p(t+1)=M\cdot p(t)=p(t)$, $p(t)$는 stationary distribution
    💡 stationary distribution(정적분포) : 초기 분포에 관계 없이 특정 시간이 지난 후, 특정한 분포에 수렴하는 것을 의미 $\rightarrow$ 시간에 따라 변하지 않는 평형 상태를 의미함

  • 즉 rank vector $r$은 고정분포로 수렴함

• Solution Eigenvector centrality 떠올리기 (Lecture 2)

  • 무방향 그래프의 adj. matrix의 Eigenvector:

    $\lambda\mathbf{c} = \mathbf{Ac}$ 를 만족하는 $\mathbf{c}$ 를 의미

    • 이는 $r = M\cdot r$과 유사한 구조로 생각해볼 수 있음
    • 단지 $M\rightarrow A$로 치환되고, 상수값(eigenvalue $\lambda$) 1이 추가된 것 뿐

  • 즉, "Flow Model"의 Equation은

    • rank vector $r$은 행렬 $M$의 eigenvector임 (eigenvalue = 1)

    • vector $u$에서 시작하여, 웹서핑을 계속 진행해나가면..
      $MM\ldots Mu$
      이는 서퍼가 네트워크에서 어디에 있을 것인가에 대한 장기적인 분포를 나타낸다고 할 수 있음
      💡 Katz Index와 연관
      $M\cdot M\ldots M$ : $M$이 인접행렬이고, 이를 거듭제곱할 시, 한 쌍의 노드 사이의 경로 수를 계산함 (장기적으론 어떤 확률분포를 나타낸다고 할 수 있음)

  • $r$이 극한이라면, flow equation $1\cdot r=M\cdot r$을 만족

  • 그렇다면 principal eigenvector $r$을 어떻게 구하는가?

    • well-known approach: Power iteration

      Initial $r^{(0)}$를 $[1/N,1/N,\ldots,1/N]$로 초기화
      Iterate $r^{(t+1)}=\mathbf{M}\cdot r^{(t)}$
      Stop $|r^{(t+1)}-r^{(t)}|_1 < \epsilon$
      L1 norm을 이용하여 적정히 수렴할때까지 반복

3. PageRank Summary

• 웹의 연결구조를 이용하여, 그래프에서 노드의 중요도를 측정
• PageRank 모델은 확률적 인접행렬 $M$을 사용하는 무작위 웹서핑
• PageRank는 $r=Mr$와 같은 행렬분해를 통해 해결할 수 있음

  $r$은 $M$의 principle eigenvector
  $M$은 랜덤워크 프로세스의 stationary distribution