CS224W 4.2 PageRank: How to Solve?

1. PageRank : How to solve?

• $n$개 노드의 그래프가 주어졌을 때, 다음과 같은 iteration을 이용할 수 있음
  • 각 노드에 initial page rank 값을 부여
  • 다음 수식(1)의 값 수렴할 때 까지 아래 update(2)를 반복함

    (1) $\sum_i |r_i^{t+1} - r_i^t|<\epsilon$
    (2) $r_j^{(t+1)}=\displaystyle\sum_{i\rightarrow j} \frac{r_i^{(t)}}{d_i}$

• Power iteration method
  • (i)초기화 : $r^0 = [1/N, \ldots ,1/N]^T$
  • (ii) 반복 : $r^{(t+1)} = M \cdot r^t$

    $r_j^{(t+1)}=\displaystyle\sum_{i\rightarrow j} \frac{r_i^{(t)}}{d_i}$ 과 동일한 수식 (4.1에서 다룸)

  • (iii) 중단(L1 norm) : $|r^{t+1} - r^t|_1<\epsilon$
    원한다면 L2 norm을 사용해도 무관.
  • 대략 50번 정도를 반복하면 수렴
  • 👇 간단한 계산 예제
    

2. PageRank : Three questions

• 수렴가능한가?
• 수렴한 값이 우리가 원하는 값인가?
• 이 결과물이 합리적인가?

3. Problems

3.1. dead ends

• out-links가 없는 dead ends

  • 투표수가 "leak out"되는 문제가 있음

  • 👇 dead end의 예제
    

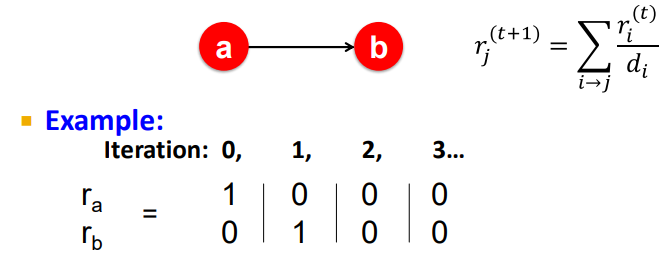
    반복을 거듭하면,
    $r_a$와 $r_b$의 중요도가 모두 0이 되어버림
    랜덤워커가 b에 도착하자마자 갈 곳이 없음

3.2. spider traps

• Spider traps : 모든 out link가 동일 그룹 내에 있는 경우
  • 모든 중요성을 흡수해버림
  • 👇 Spider Trap의 예제
    

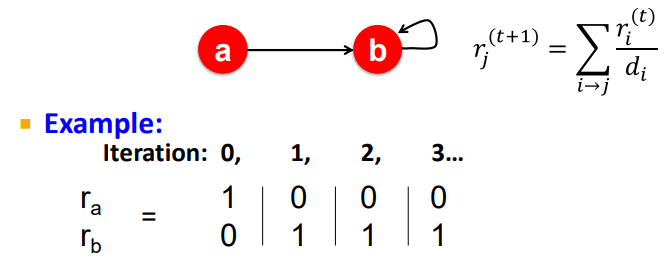
    반복을 거듭하면,
    $r_a$는 중요도 0이 되고, $r_b$는 중요도 1을 갖게 됨
    어떤 경로를 통해 b 노드에 도달한 이후엔, surfer가 b에 영원히 갇히기 때문에 이와 같은 문제가 발생

4. Solutions

4.1. Spider trap의 솔루션 : 무작위 점프

• 매순간 두 가지 옵션 중 선택
  • $\beta$ 확률로, link를 따라 랜덤하게 이동
  • $1-\beta$ 확률로, 랜덤한 페이지로 무작위 점프
  • 일반적으로 $\beta$는 0.8~0.9 사이로 정의
• 이에 따라 Surfer는 spider trap으로부터 몇 스텝 안에 벗어날 수 있음

4.2. Dead end의 솔루션 : 순간이동

• dead ends인 노드는 열의 합이 모두 0임 (out-links가 없기 때문에)
• 이는 확률론적 인접행렬이라 말할 수 없음
  • 확률론적 인접행렬의 열의 합은 모두 $1$이 되어야 함을 전제하므로, 이에 위배됨
• 이를 해결하기 위하여, 합이 0인 열의 값들을 $1/N$의 값으로 균등하게 조정하여 해결 가능
  

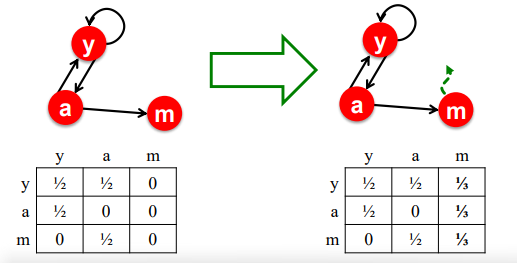
4.3. 텔레포트 방식이 문제를 해결할 수 있는 이유?

4.3.1. Spider의 경우

• Trap에 갇히면, 노드의 중요도가 원한 값이 아니게 된다는 문제

  Spider-traps은 그 자체는 문제가 아니지만, trap에 갇히는 경우 어떤 페이지의 중요도가 1이 되고, 어떤 페이지는 0이 되기 때문에, Score 자체가 우리가 원한 값이 아니라는 문제가 있음

• 모든 노드가 (적은 수치이더라도) 어느 정도의 중요도를 갖고있기를 원함
• Solution 텔레포트를 통해 몇 스텝이 지나면 더이상 trap에 갇히지 않게 되므로 이 문제는 해결됨

4.3.2. Dead-ends의 경우

• 인접행렬 $M$이 column stochastic하지 않기 때문에, 초기 가정과 배반되는 문제
• Solution 더이상 갈 곳이 없는 dead-ends에 도착하면, $M$을 column stochastic하게 변경(텔레포트하게 변경)하여 이 문제를 해결

4.4. Google's Solution

• PageRank equation

  $r_i = \displaystyle\sum_{i\rightarrow j} \beta \frac{r_i}{d_i} + (1-\beta)\frac{1}{N}$

  • $d_i$는 node $i$의 out-degree
    dead-ends는 사전에 제거되었거나, 도달할 때 랜덤순간이동하는 것을 가정함

• 위 형태를 Matrix formulation 형태로 재정의한다면?

  $P = \beta M + (1-\beta)\left[\frac{1}{N}\right]_{N\times N}$
  동일하게 재귀적 문제로 정의할 수 있으므로,
  $r = G\cdot r$ Power iteration 동일하게 동작
  $\beta=0.8\sim 0.9$

• 👇 Random Teleports $(\beta=0.8)$ 예제
  

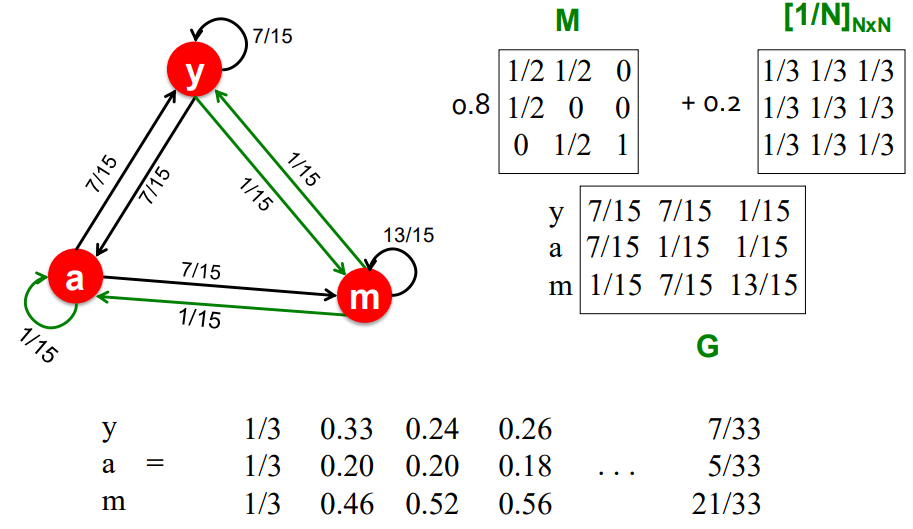
5. Summary

• PageRank는 $r=Gr$을 이용하여 문제를 해결
  • stochastic adjacency matrix $G$의 power iteration을 통해 효율적으로 연산 할 수 있다는 점!
• 순간이동(random uniform teleportation)을 통해 dead-ends 와 spider-traps 문제를 해결