ML - 4

모델 평가

분류 모델 평가 방법

회귀 모델과 분류 모델의 성능을 평가할때 회귀 같은 경우는 에러치를 계산하면 되므로 비교적 간단하다.

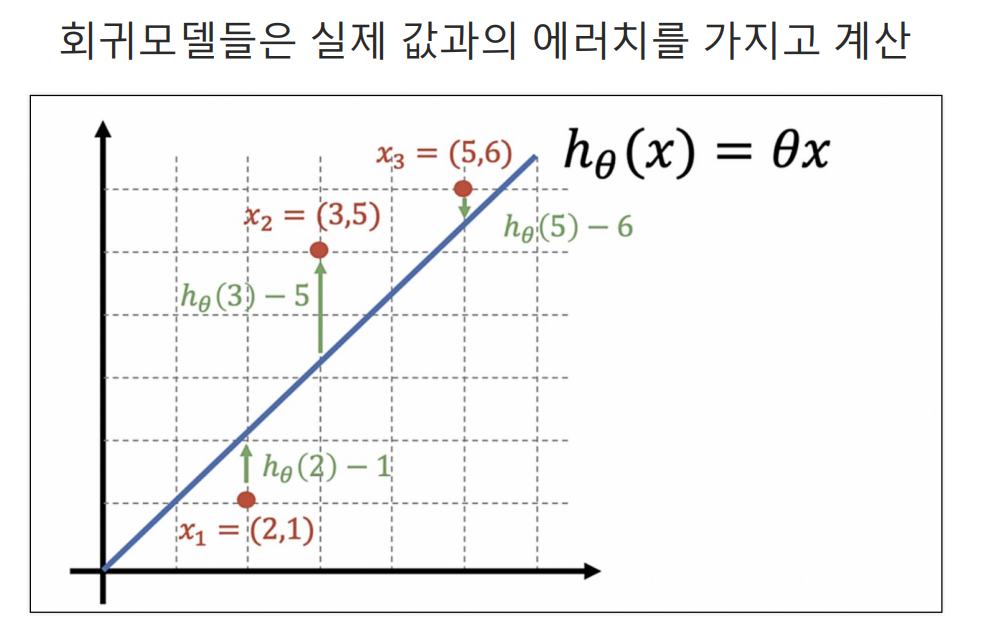
하지만 분류모델의 경우에는 평가 항목이 많아 쉽지가 않다.

이런 분류 모델 평가에서 TP (True Positive), TN (True Negative), FP (False Positive), FN (False Negative)은 이를 가능케 하는 중요한 지표로

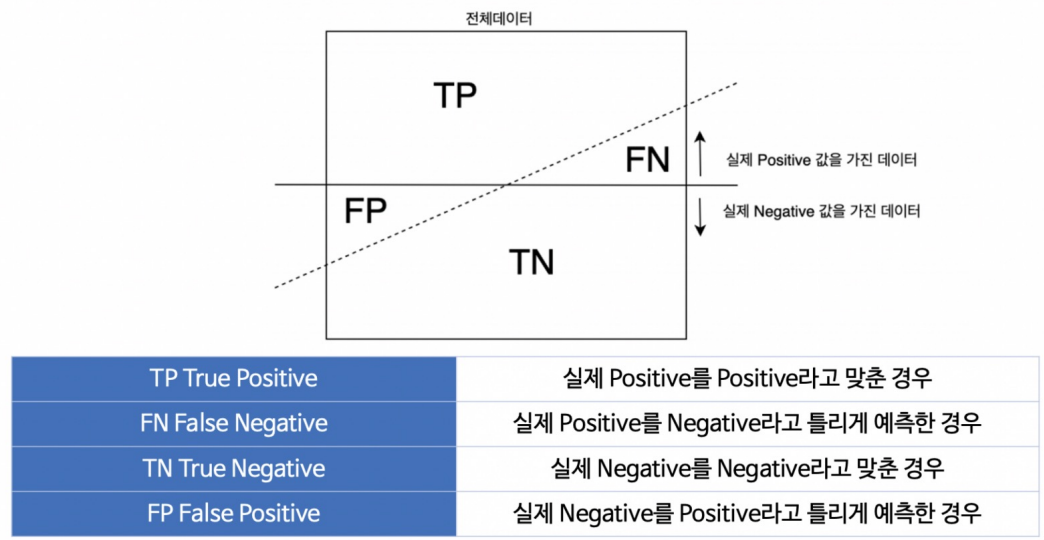
TP, TN, FP, FN은 분류 모델의 성능을 정량적으로 평가하는 데 사용됩니다. 이 네 가지 개념은 모델이 예측한 결과와 실제 데이터의 차이를 나타냅니다. TP는 모델이 실제로 정확히 예측한 양성 샘플의 수, TN은 음성 샘플의 정확한 예측 수, FP는 모델이 양성으로 잘못 예측한 수, FN은 음성으로 잘못 예측한 수를 나타냅니다. 이를 통해 정확도, 정밀도, 재현율 등의 성능 지표를 계산하여 모델의 품질을 평가할 수 있습니다.

이해를 돕는 사진

TYPE 1 ERROR를 FP 라고하고
TYPE 2 ERROR를 FN 이라고함

Precision

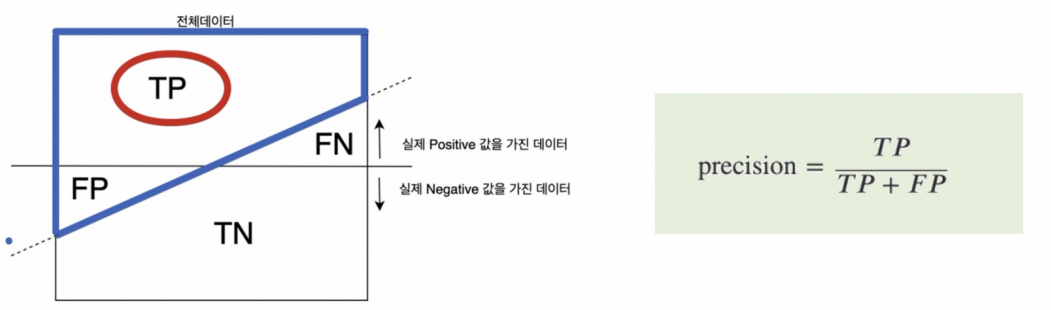
• Precision은 양성으로 예측한 샘플 중에서 실제로 양성인 비율을 나타냅니다. 즉, 양성으로 예측한 것 중에서 얼마나 정확한지를 측정하는 지표로, 높을수록 모델의 양성 예측이 신뢰성 있습니다.
• 1이라고 예측한 것들중에서 실제 1의 비율

RECALL

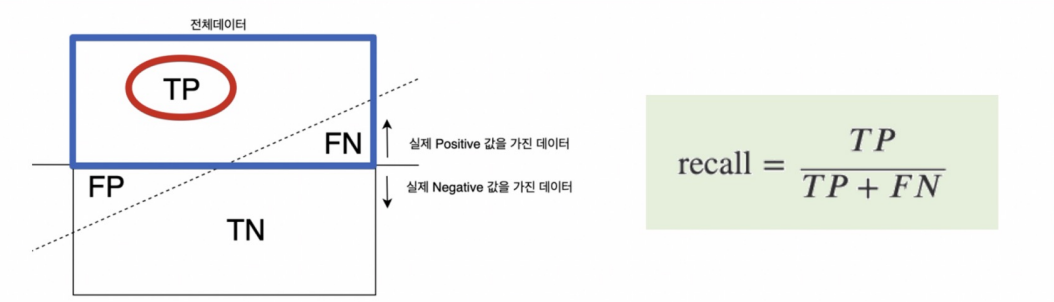
• Recall은 실제 양성인 샘플 중에서 모델이 양성으로 정확하게 예측한 비율을 나타냅니다. 즉, 실제 양성 중에서 얼마나 많이 감지할 수 있는지를 측정하는 지표로, 높을수록 모델이 양성을 잘 감지합니다.
• 실제 1인 데이터중에 1이라고 예측한 비율

FALLOUT

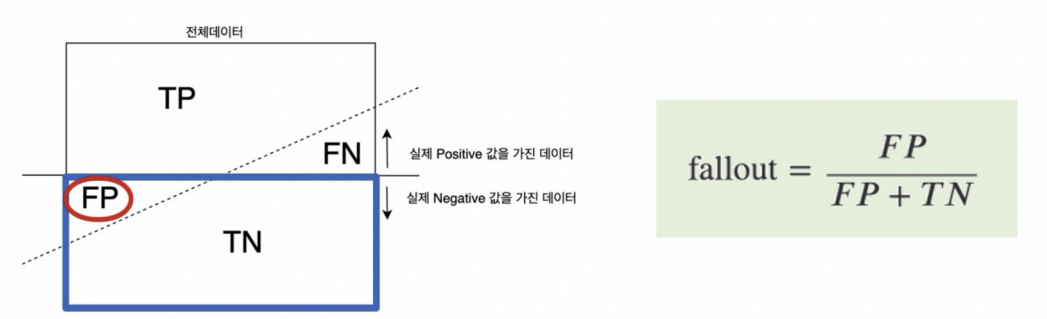
• Fallout은 실제로 음성인 샘플 중에서 모델이 양성으로 잘못 예측한 비율을 나타냅니다. 즉, 실제 음성 중에서 얼마나 많이 오검출하는지를 측정하는 지표로, 낮을수록 모델이 음성을 잘 유지하는 경향이 있습니다.
• 0이라고 예측한 것들중에서 실제 1의 비율

Threshold

Threshold(임계값)은 분류 모델에서 양성(Positive) 또는 음성(Negative)으로 예측하는 기준을 나타냅니다. 모델의 출력은 일반적으로 연속적인 값으로 나오는데, 이를 양성 또는 음성으로 분류하기 위해 Threshold를 적용합니다.

Threshold = 0.5 일때 예시

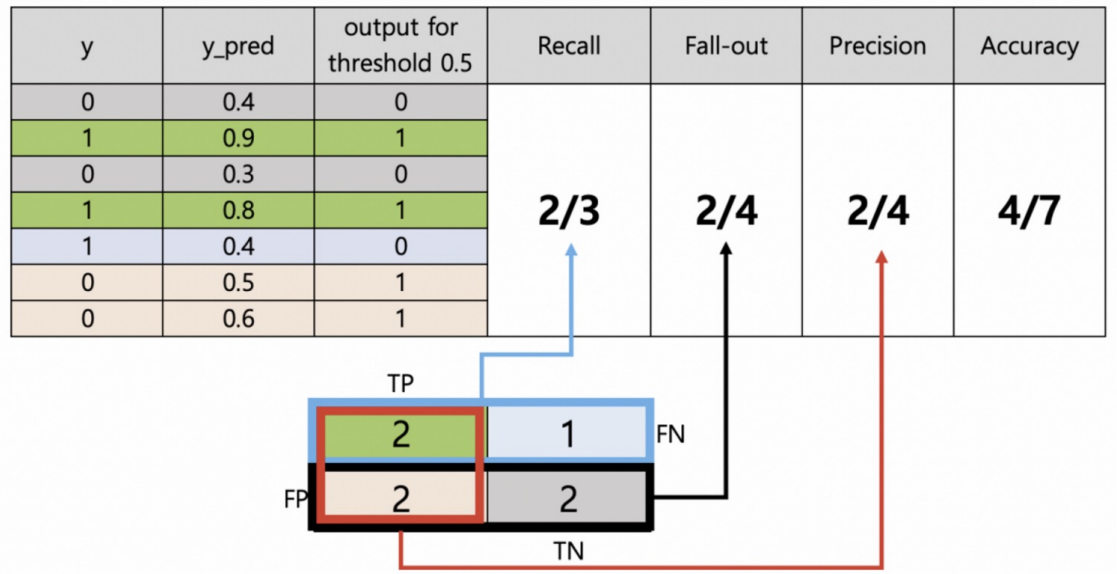
일반적으로 모델의 출력이 Threshold보다 크면 양성으로, 작으면 음성으로 분류됩니다. 이 Threshold 값을 조정하면 모델의 성능과 예측 결과가 달라집니다. 높은 Threshold는 더 높은 정밀도와 낮은 재현율을 가져올 수 있고, 낮은 Threshold는 그 반대의 결과를 가져올 수 있습니다.

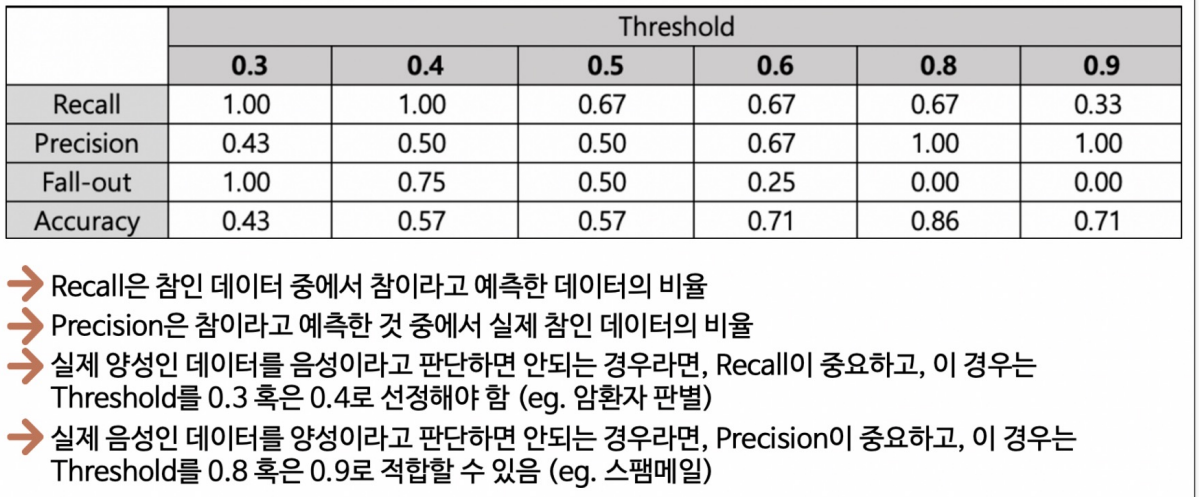
Threshold의 조정은 모델의 성능과 비즈니스 요구 사항에 따라 적절히 설정되어야 합니다. 예를 들어, 의료 분야에서는 높은 정밀도가 중요할 수 있으므로 높은 Threshold를 선택할 수 있습니다. 반면, 금융 분야에서는 재현율이 더 중요할 수 있어 낮은 Threshold를 선택할 수 있습니다. Threshold의 조정은 모델을 튜닝하여 비즈니스 목표에 가장 적합한 예측을 얻을 수 있도록 도와줍니다.

F1-SCORE

F1-Score는 분류 모델의 성능을 종합적으로 평가하기 위한 지표로, 정밀도(Precision)와 재현율(Recall)의 조화 평균을 나타냅니다.

ROC 곡선

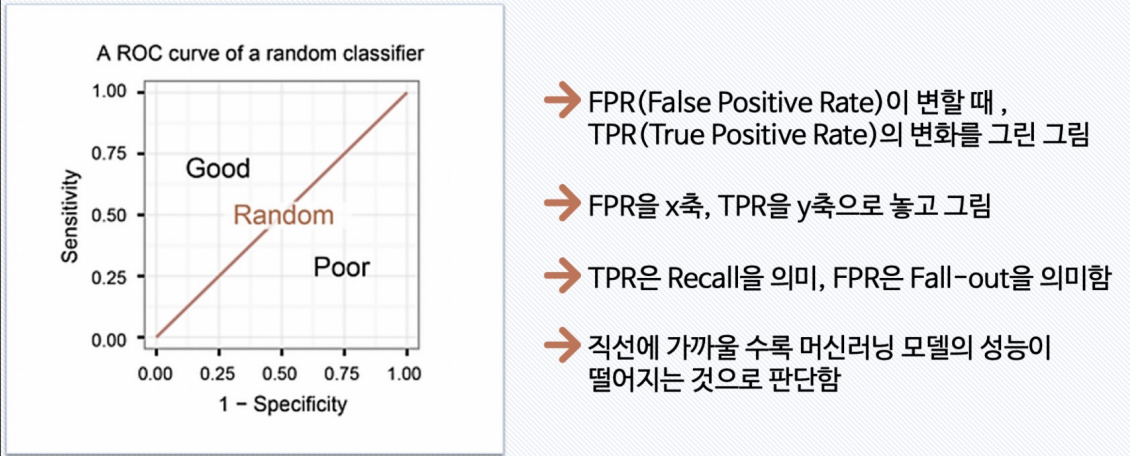
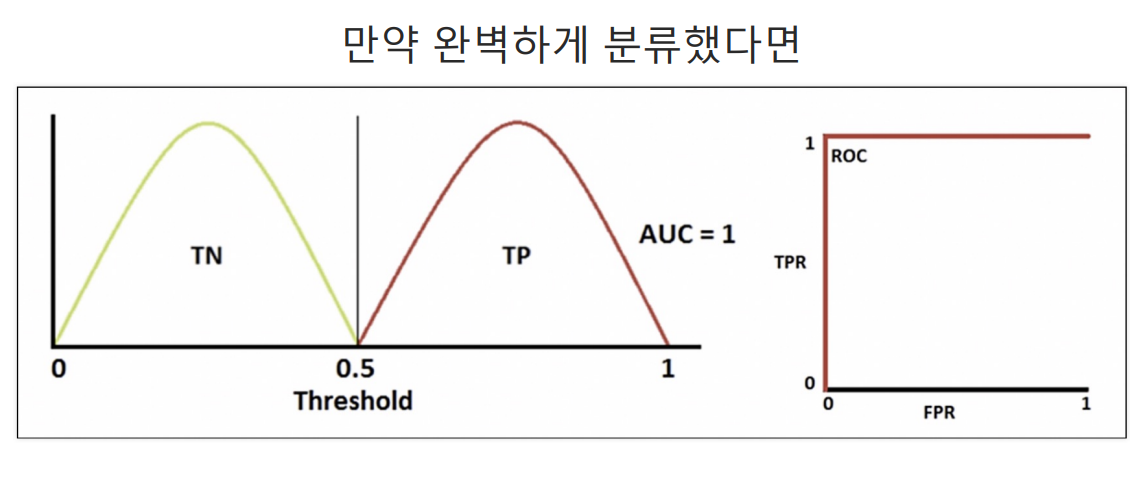
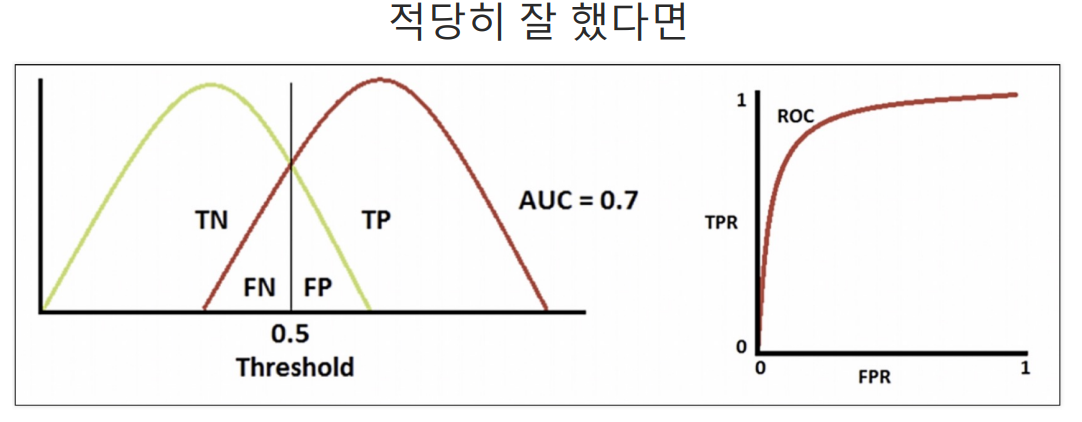
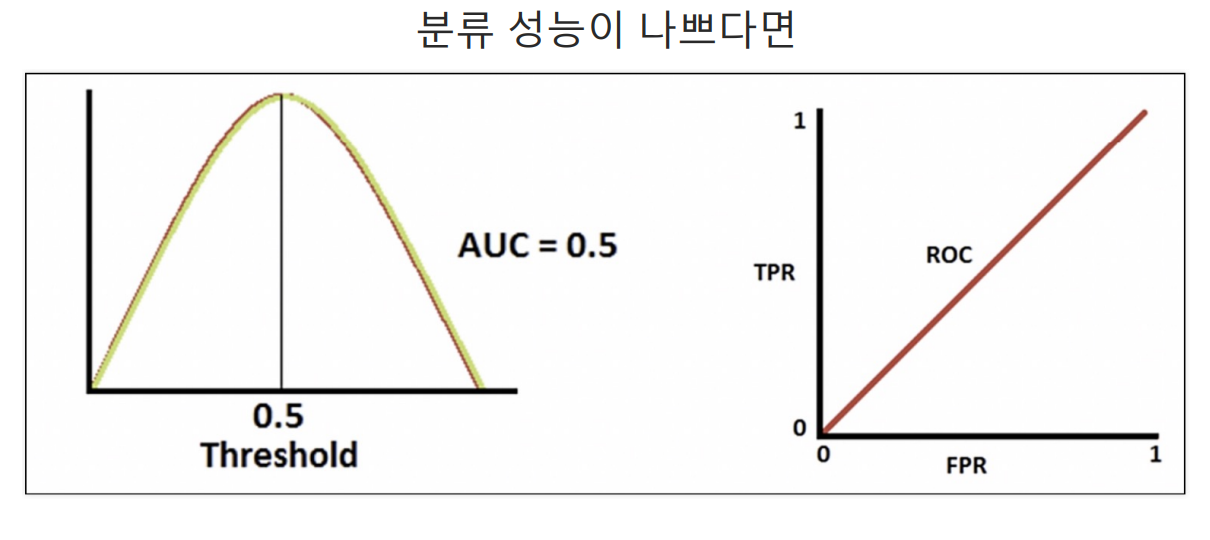
파이썬 코드로 확인해기

import pandas as pd

red_wine = pd.read_csv('winequality-red.csv', sep=';')
white_wine = pd.read_csv('winequality-white.csv', sep=';')
red_wine['color'] = 1
white_wine['color'] = 0

wine = pd.concat([red_wine, white_wine])

wine['taste'] = [1. if grade > 5 else 0 for grade in wine['quality']]

x = wine.drop(['taste','quality'], axis= 1)
y = wine['taste']

from sklearn.metrics import accuracy_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=13)

wine_tree = DecisionTreeClassifier(max_depth=2, random_state=13)
wine_tree.fit(x_train, y_train)

y_pred_tr = wine_tree.predict(x_train)
y_pred_test = wine_tree.predict(x_test)

지난번에 와인 분류할때 썻던 코드를 가져온 뒤 모델 검증을 위해 sklearn의 accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, roc_curve 라이브러리를 불러와 줍니다.

from sklearn.metrics import accuracy_score, precision_score
from sklearn.metrics import recall_score, f1_score
from sklearn.metrics import roc_auc_score, roc_curve

print('Accuracy :', accuracy_score(y_test, y_pred_test))
print('Recall :', recall_score(y_test, y_pred_test))
print('Precision :', precision_score(y_test, y_pred_test))
print('AUC Score :', roc_auc_score(y_test, y_pred_test))
print('F1 Score :', f1_score(y_test, y_pred_test))

Accuracy : 0.7161538461538461
Recall : 0.7314702308626975
Precision : 0.8026666666666666
AUC Score : 0.7105988470875331
F1 Score : 0.7654164017800381

# 결과 값들중 1인 경우의 컬럼만 가져옴!!
pred_proba = wine_tree.predict_proba(x_test)[:, 1]

# fpr : 특이도로, 실제 음성 중 양성으로 잘못 분류된 비율
# tpr : 실제 양성 중에서 정확히 양성으로 분류된 비율
# thresholds: ROC 곡선을 생성하는 데 사용되는 각 임계값

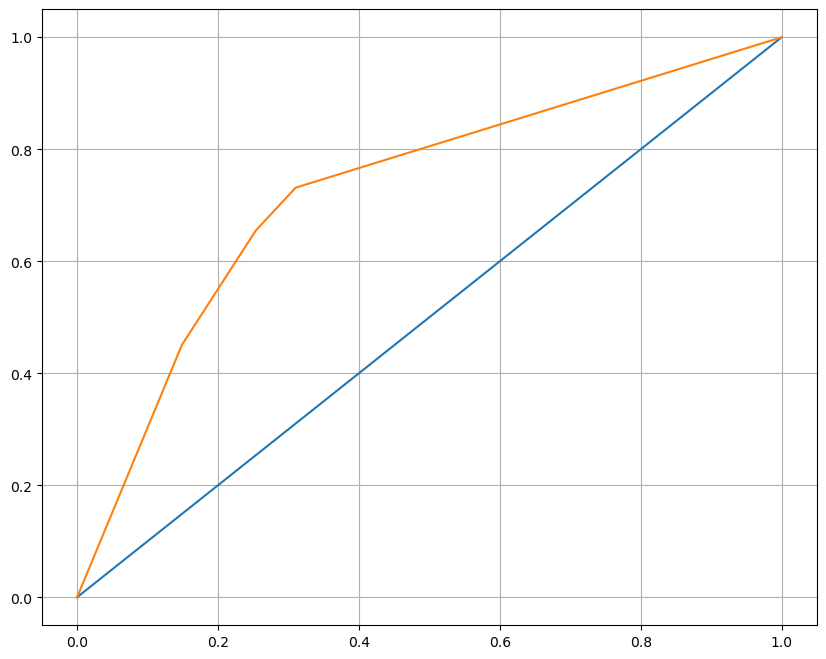
fpr, tpr, thresholds = roc_curve(y_test, pred_proba)

plt.figure(figsize=(10,8))
plt.plot([0,1], [0,1])
plt.plot(fpr, tpr)
plt.grid()
plt.show()

wine_tree 모델의 검증 결과중에 참이라고 판단한 데이터들을 불러와 y_test와 비교하여 fpr, tpr과 thresholds을 구해 시각화 해줫습니다.

수학 함수

파이썬을 이용하여 머신러닝을 하는데 필요한 함수를 그리는 법을 학습하였습니다.

2차함수

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.style.use('seaborn-whitegrid')

x = np.linspace(-3, 2, 100)
y1 = 3 * x**2 + 2
y2 = 3 * (x+1)**2 + 2

plt.figure(figsize=(12,8))
plt.plot(x,y1, lw=2, ls='dashed', label='$y=3x^2 + 2$')
plt.plot(x,y2, label='$y=3(x+1)^2 + 2$')
plt.legend(fontsize=15)
plt.xlabel('$x$', fontsize=25)
plt.ylabel('$y$', fontsize=25)
plt.show()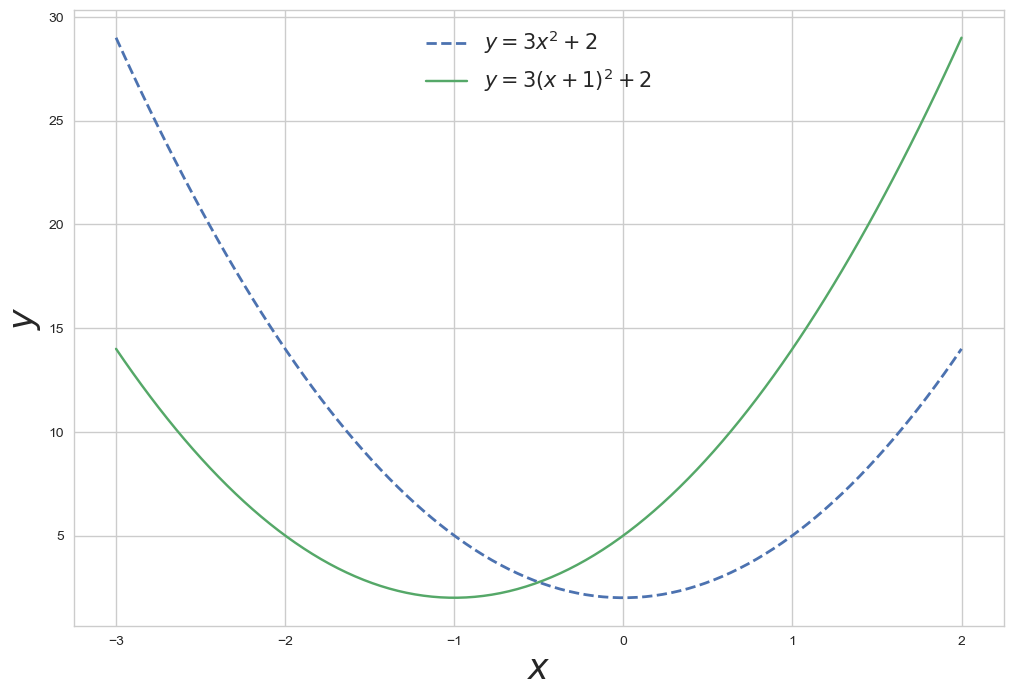

• np.linspace을 사용하여 -3에서 2까지의 100개의 연속된 변수를 생성함
• 라벨에 $$를 쓴 다음 변수를 적어주면 문자식이 수학식으로 변환됩니다.

지수 함수

x = np.linspace(-2, 2, 100)

a11, a12, a13 = 2, 3, 4
y11, y12, y13 = a11**x, a12**x, a13**x

a21, a22, a23 = 1/2, 1/3, 1/4
y21, y22, y23 = a21**x, a22**x, a23**x

fig, ax = plt.subplots(1,2, figsize=(12, 6))

ax[0].plot(x, y11, color='k', label='$2^x$')
ax[0].plot(x, y12, '--', color='k', label='$3^x$')
ax[0].plot(x, y13, ':', color='k', label='$4^x$')
ax[0].legend(fontsize=20)

ax[1].plot(x, y21, color='k', label='$(1/2)^x$')
ax[1].plot(x, y22, '--', color='k', label='$(1/3)^x$')
ax[1].plot(x, y23, ':', color='k', label='$(1/4)^x$')
ax[1].legend(fontsize=20)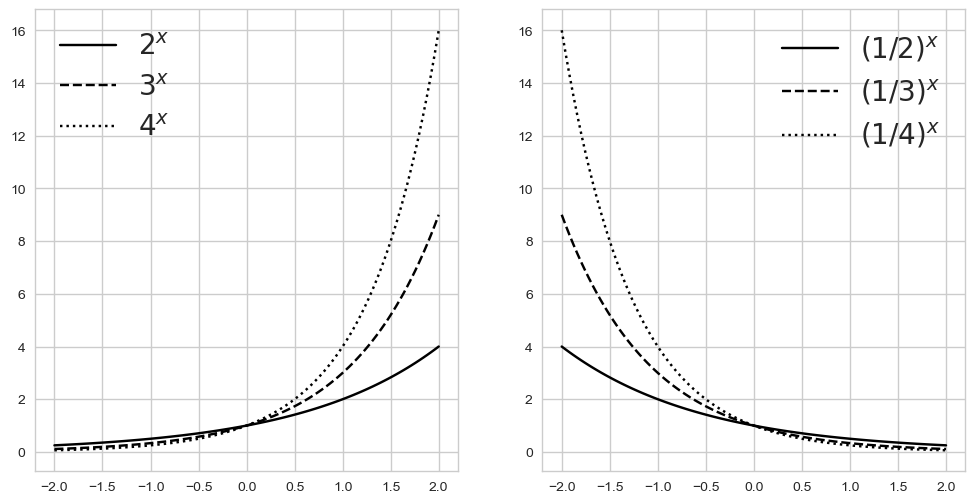

• subplots를 사용하여 1행 2열의 그래프를 그릴 것을 선언함

로그 함수

def log(x, base):
    return np.log(x)/np.log(base)

로그 함수의 밑수를 바꾸는 기능이 numpy에 없어 밑수를 바꾸는 함수를 만들어줌!!

x1 = np.linspace(0.001, 5, 1000)
x2 = np.linspace(0.01, 5, 100)

y11 , y12 = log(x1, 10), log(x2, np.e)
y21 , y22 = log(x1, 1/10), log(x2, 1/np.e)

fig, ax = plt.subplots(1,2, figsize=(12, 6))

ax[0].plot(x1, y11, color='k', label=r'$\log_{10} x$')
ax[0].plot(x2, y12, '--', color='k', label=r'$\log_{e} x$')

ax[0].set_xlabel('$x$', fontsize=25)
ax[0].set_ylabel('$y$', fontsize=25)
ax[0].legend(fontsize=20, loc='lower right')

ax[1].plot(x1, y21, color='k', label=r'$\log_{1/10} x$')
ax[1].plot(x2, y22, '--', color='k', label=r'$\log_{1/e} x$')

ax[1].set_xlabel('$x$', fontsize=25)
ax[1].set_ylabel('$y$', fontsize=25)
ax[1].legend(fontsize=20, loc='upper right')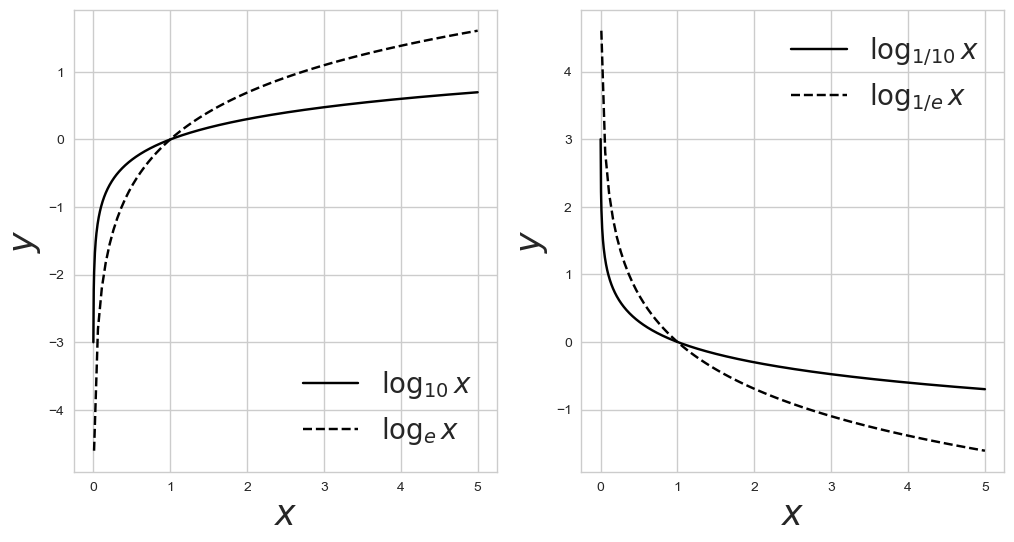

• 라벨에 표시할 때 로그가 하나의 기호이므로 다음과 같이 써줌

  $\log_{e} x$
  $ \log_{e} x $

시그모이드 함수

시그모이드 함수는 S 모양의 곡선을 가지며, 입력값이 큰 양수일 때 1에 수렴하고, 큰 음수일 때 0에 수렴합니다. 이는 주로 이진 분류 문제에서 확률을 나타내는 데 사용되며, 입력값을 확률로 변환하는 특성을 갖습니다. 또한, 미분이 가능하여 경사 하강법과 같은 최적화 알고리즘에서 자주 활용됩니다.

z = np.linspace(-10, 10, 100)
sigma = 1/(1+np.exp(-z))

plt.figure(figsize=(12,8))
plt.plot(z, sigma)
plt.xlabel('$z$', fontsize=25)
plt.ylabel('$\sigma(z)$', fontsize=25)
plt.show()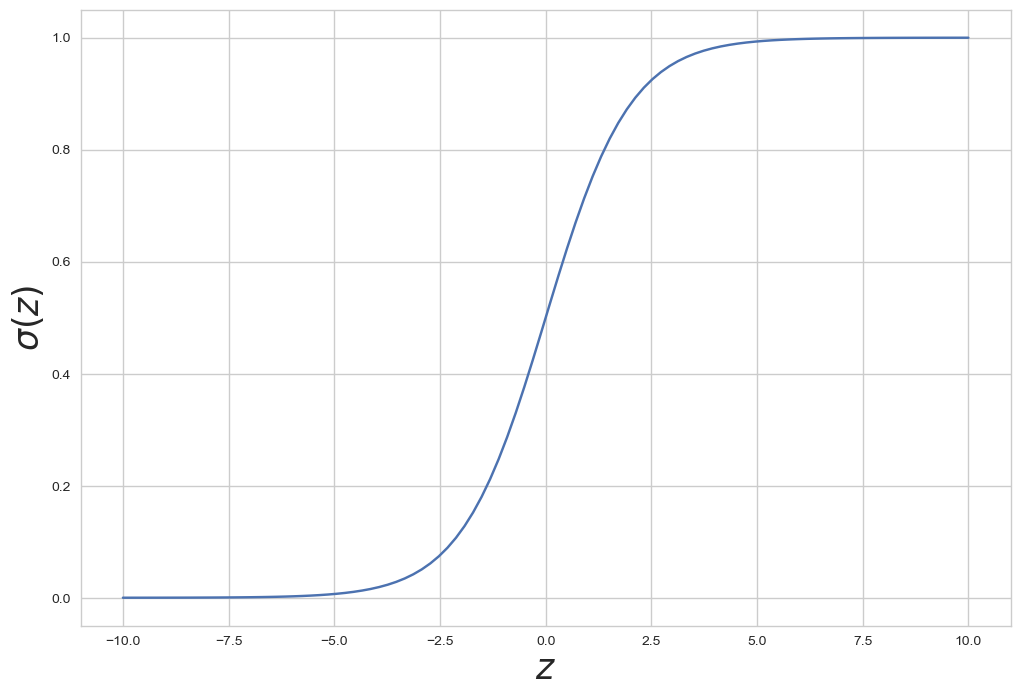

함수식

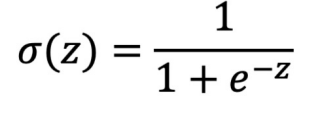
함수 표현

백터

벡터의 표현

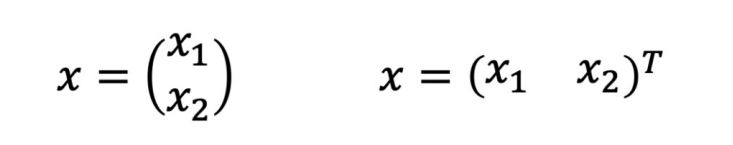
다변수 벡터함수의 예제

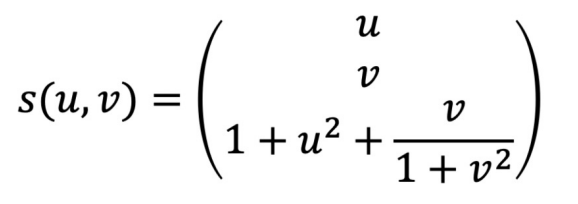
스칼라

단일 변수 스칼라 함수

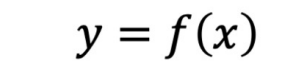
다중 변수 스칼라 함수

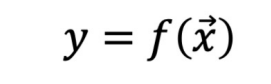
다변수 벡터함수

u = np.linspace(0,1,30)
v = np.linspace(0,1,30)
U, V = np.meshgrid(u, v)

X = U
Y = V
Z = (1+U**2) + V/(1+V**2)

fig = plt.figure(figsize=(7,7))
ax = plt.axes(projection='3d')

ax.xaxis.set_tick_params(labelsize=15)
ax.yaxis.set_tick_params(labelsize=15)
ax.zaxis.set_tick_params(labelsize=15)


ax.set_xlabel('$x$',fontsize=15)
ax.set_ylabel('$y$',fontsize=15)
ax.set_zlabel('$z$',fontsize=15)

ax.scatter3D(X, Y, Z, marker='.', color='gray')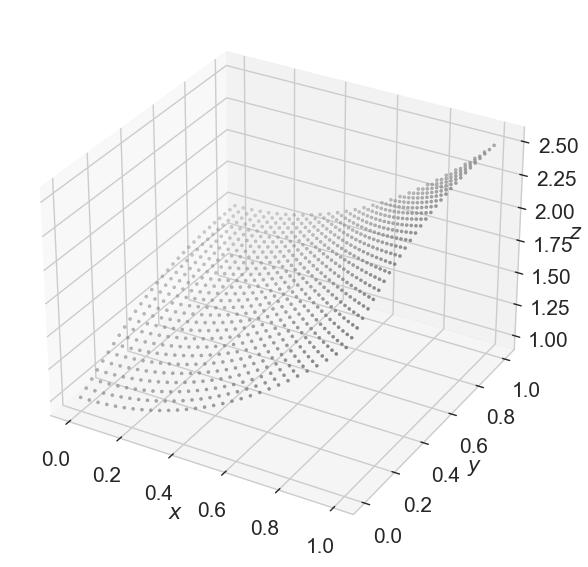

3차원 함수를 그릴수 있게됨

• 변수가 여러개 이므로 x, y, z로 변수를 3개 지정해줌
• plt.axes(projection='3d')로 지정하여 3d 그레프를 작성함

표현 방식

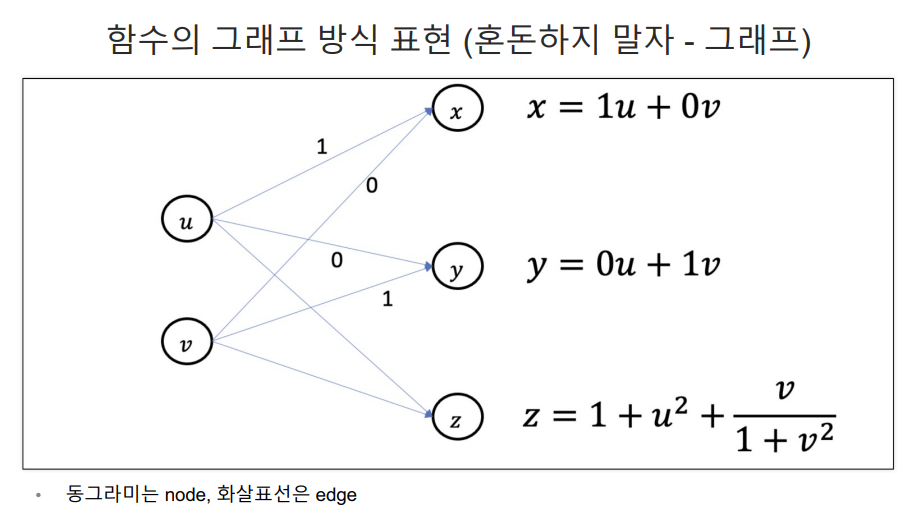
합성함수

합성 함수는 두 개 이상의 함수를 조합하여 새로운 함수를 만드는 과정을 나타냅니다. 만약 함수 f(x)와 함수 g(x)가 있다면, 이들을 합성한 함수 h(x)는 h(x)=f(g(x))와 같이 표현됩니다. 즉, g(x)의 출력을 f(x)의 입력으로 사용하여 새로운 함수를 만드는 것이 합성 함수입니다. 이를 통해 다양한 함수를 조합하여 더 복잡한 함수를 만들 수 있습니다.

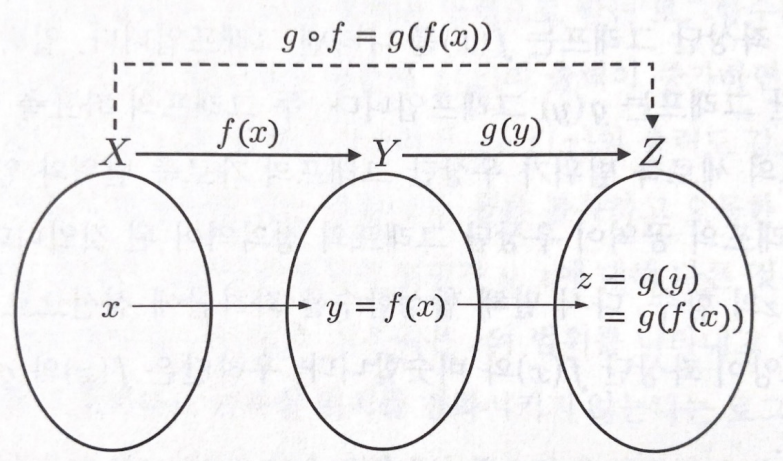
x = np.linspace(-4, 4, 100)
y = x**3 - 15*x + 30
z = np.log(y)

fig, ax = plt.subplots(1, 2, figsize=(12, 6))

ax[0].plot(x, y, label=r'$x^3 - 15x + 30$', color='k')
ax[0].legend(fontsize=18)

ax[1].plot(y, z, label=r'$\log(y)$', color='k')
ax[1].legend(fontsize=18)

plt.show()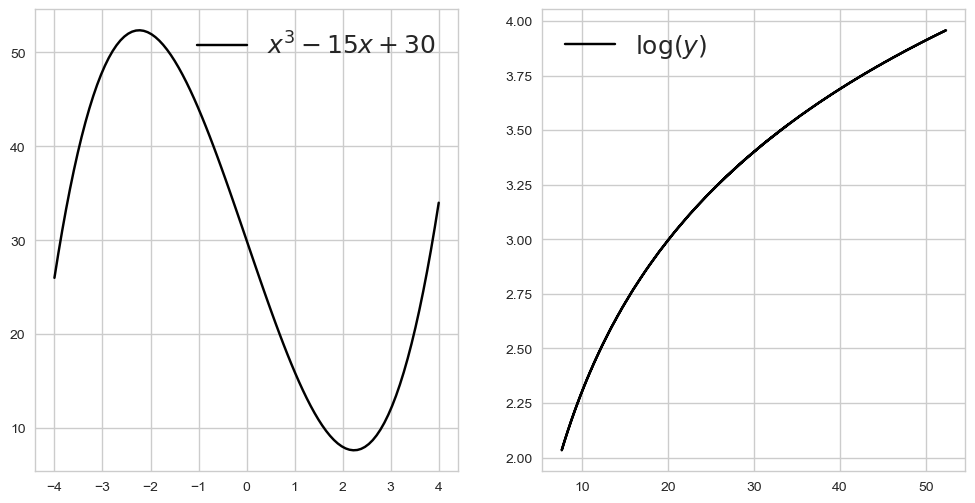

Boxplot의 해석방법

Boxplot은 데이터의 분포를 시각적으로 표현하는 그래픽 방법 중 하나입니다. Boxplot의 주요 구성 요소와 해석 방법을 이해하기 쉽게 설명하겠습니다:

상자 (Box): 상자는 데이터의 중간 50%를 나타냅니다. 상자의 하단과 상단은 각각 1사분위수(Q1)와 3사분위수(Q3)를 나타냅니다. 상자의 높이는 데이터의 중간 50% 범위를 나타내며, 상자 중앙의 선은 중앙값(median)을 나타냅니다.

수염 (Whiskers): 수염은 전체 데이터 범위를 나타냅니다. 일반적으로 1.5배 사분위 범위(IQR)까지만 수염으로 표시하고, 이 범위를 벗어나는 값은 이상치(outlier)로 간주됩니다.

이상치 (Outliers): 상자와 수염 외부에 표시되는 점은 이상치를 나타냅니다. 이상치는 데이터의 일반적인 분포에서 크게 벗어난 값으로 볼 수 있습니다.

상자의 길이와 분포의 변동성: 상자의 길이가 짧을수록 데이터가 밀집되어 있고, 길면 데이터가 퍼져있음을 나타냅니다. 분포의 변동성을 시각적으로 확인할 수 있습니다.

Boxplot은 데이터의 중심 경향 및 분포의 형태를 빠르게 파악할 수 있어 많이 사용되며, 다양한 그룹 간 비교나 이상치 탐지에 유용합니다.

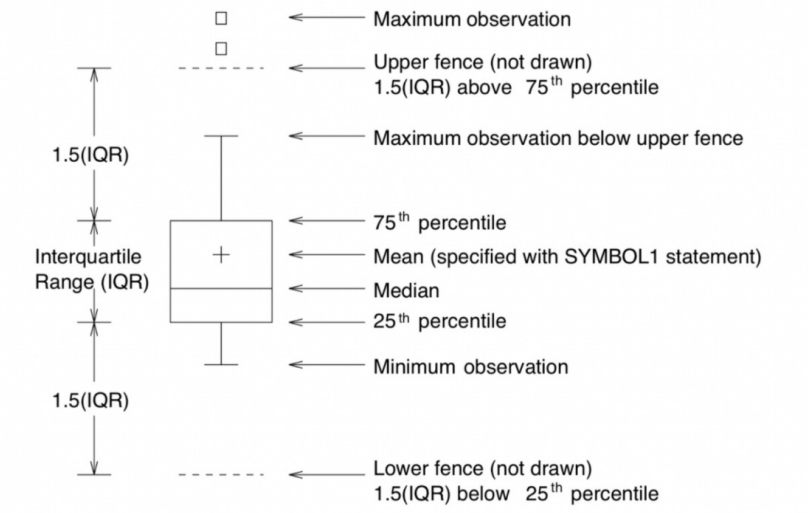
예시

import matplotlib.pyplot as plt
samples = [1,7,9,16,36,39,45,45,46,48,51,100, 101]
tmp_y = [1]*len(samples)

plt.figure(figsize=(12,4))
plt.scatter(samples, tmp_y)
plt.grid()
plt.show()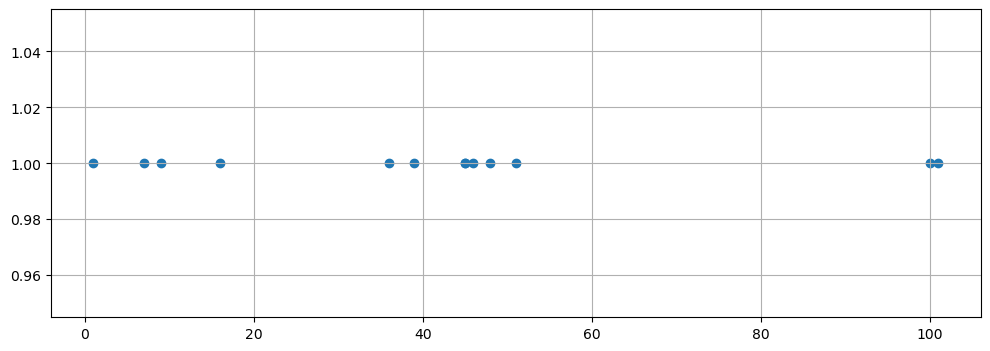

# 중간값
import numpy as np
np.median(samples)

# 25프로 지점 찾기
np.percentile(samples, 25)
# 75프로 지점 찾기
np.percentile(samples, 75)
# 중앙값 찾기
np.percentile(samples, 75) - np.percentile(samples, 25)
# IQR
upper_fence = q3 + iqr*1.5
# IQR
lower_fence = q1 - iqr*1.5


plt.figure(figsize=(12,4))
plt.scatter(samples, tmp_y)
plt.axvline(x=q1, color='black')
plt.axvline(x=q2, color='black')
plt.axvline(x=q3, color='black')
plt.axvline(x=upper_fence, color='black', ls='dashed')
plt.axvline(x=lower_fence, color='black', ls='dashed')
plt.grid()
plt.show()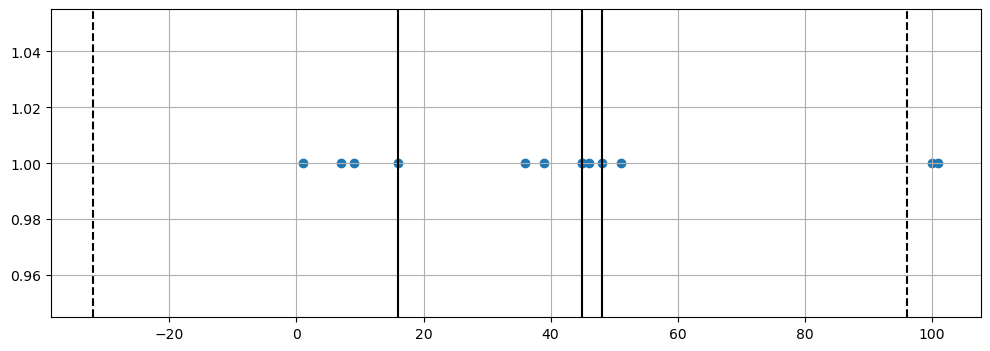

쉽게 그리기

import seaborn as sns
plt.figure(figsize=(12,4))
sns.boxplot(samples)
plt.grid()
plt.show()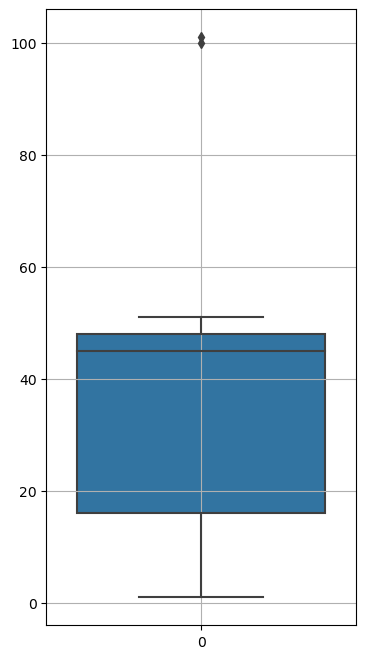

전체 코드

모델 평가 전체코드

수학 함수 전체코드

Boxplot 전체코드

그림 출처 제로베이스