자료구조와 알고리즘의 콜라보, 힙 정렬(Heap Sort)

Eddy·2022년 2월 1일

algorithm

정렬로 알고리즘 공부하기

목록 보기

4/4

여태까지 우리는 주어진 데이터를 정렬된 데이터로 가공하는 '절차'에 초점을 맞췄다.

하지만 주어진 데이터를 스마트하게 '정리'하는 방법에 초점을 맞춰보면 어떨까?

바로 '자료 구조(Data structure)'다.

자료 구조는 말 그대로 데이터에 구조를 만드는 방법이다.

실생활에서 물건을 관리할 때도
우리는 일정한 체계를 부여해서 정리를 한다.

수많은 양말을 어떻게 서랍에 넣어놓을지.

책을 책장에 어떻게 꽂아놓아야 할지.

냉장고에 반찬을 어떤 배치로 넣어놓을지.

등등...

왜 이런 체계를 굳이 정해야 할까?

왜냐하면 우리가 어떤 방식으로 자료를 정리해뒀는지에 따라서,
자료를 꺼내거나, 지우거나, 가장 오래된 자료를 찾거나... 등등
여러가지 작업의 효율이 달라지기 때문이다.

양말을 아무렇게나 넣어둘 수도 있지만,
색깔별로 다른 서랍에 넣어놓는다면 매번 양말을 찾는 작업이 훨씬 빨라진다.

마찬가지로 프로그래밍에서도 적합한 자료 구조를 사용하면,
알고리즘이 문제를 빠르고 효율적으로 해결할 수 있다.

자료구조와 알고리즘은 항상 같이 다니는 실과 바늘 같은 관계다.

힙 정렬(Heap sort)은 자료구조와 알고리즘의 콜라보를 통해
문제를 멋지게 해결한 대표적인 사례라고 할 수 있다.

(주의) 힙 정렬에서 말하는 '힙'과 메모리 할당 공간인 '힙'은 관련이 없다.

완전 이진 트리

힙 정렬을 이해하기 위해서
완전 이진 트리부터 시작해보자.

그냥 '이진 트리'라고 하면 자식 노드가 2개 이하로만 연결된 트리를 말한다.

가지가 2개씩 갈라지는 포도송이 같이 생겼다.

완전 이진 트리는,
이진 트리인데 중간중간 빈 송이가 없이 꽉 찬 포도송이라고 할 수 있다.

완전 이진 트리는 마지막 층만 제외하고는 모든 층에 노드가 꽉 차있다.
마지막 층도 왼쪽부터 순서대로 데이터가 채워진다.
즉, 맨 오른쪽에는 비어있을 수 있지만 중간에는 비어있으면 안 된다.

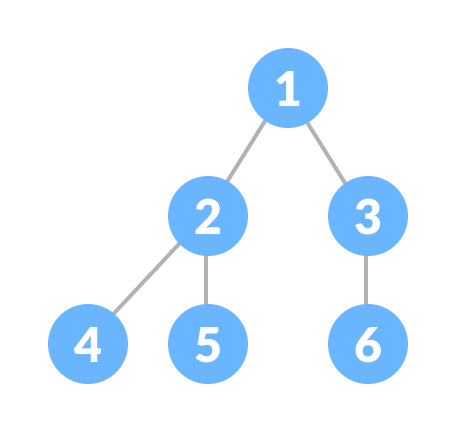
(출처: programiz)

이 트리는 마지막 층의 맨 오른쪽만 빼고
노드가 다 차있기 때문에 완전 이진 트리다.

완전 이진 트리를 표현한 배열

완전 이진 트리는 배열로 간단하게 표현할 수 있다.

트리인데 어떻게 배열로 표현하지?

완전 이진 트리는 위에서부터, 왼쪽부터 채워지기 때문에
거기에 맞춰서 번호를 매길 수 있다.

그리고 이 번호를 인덱스로 사용해서 배열에 집어넣으면,
이진 트리를 표현한 배열이 되는 것이다.

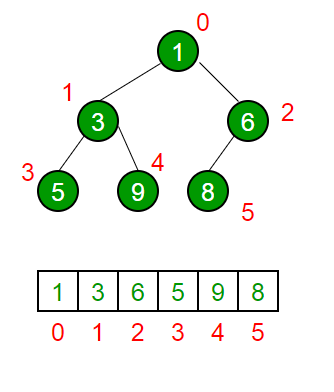
(출처: geeksforgeeks)

간단한 식으로 인덱스 구하기

완전 이진 트리로 표현한 배열은 아주 편리한 장점이 하나 있다.

어떤 노드의 인덱스 번호를 알고 있다면,
그 노드의 부모 노드와 자식 노드에 바로 접근할 수 있다.

트리의 각 층마다 노드 개수가 2배씩 늘어나고,
한 노드에 2개의 자식 노드가 있기 때문이다.

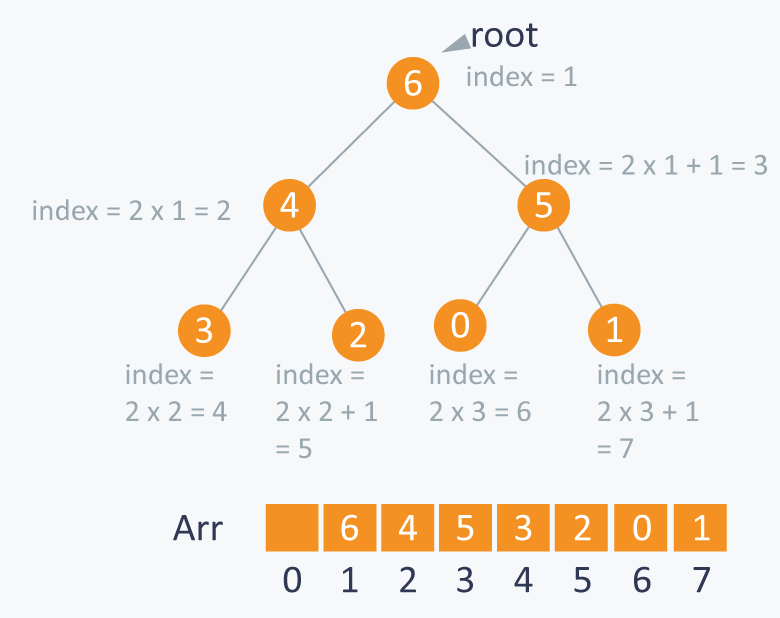
(출처: hackerEarth)

위 그림에서 보듯이 부모 노드와 자식 노드의 인덱스는 항상 일정한 규칙을 띈다.
(1에서 시작하는 index일 경우)

i 노드의 부모 노드 인덱스 = i / 2

i 노드의 왼쪽 자식 노드 인덱스 = 2i

i 노드의 오른쪽 자식 노드 인덱스 = 2i + 1

만약 '인덱스가 0에서 시작할 경우'에는
왼쪽이 2i+1, 오른쪽이 2i+2가 된다.
부모 노드는 어차피 나머지를 버리는 나눗셈 연산(/)이기 때문에 같다.

간단하니까 아래에 주어지는 그림을 보고 머릿속으로 한번 계산해보자.

1번 노드의 부모 인덱스는?
2번 노드의 왼쪽 자식 인덱스는?
1번 노드의 오른쪽 자식 인덱스는?

(출처: geeksforgeeks)

1번 노드의 부모 인덱스: 1 / 2 = 0
2번 노드의 왼쪽 자식 인덱스: 2 * 2 + 1 = 5
1번 노드의 오른쪽 자식 인덱스: 2 * 1 + 2 = 4

최소/최대 조건

힙을 구성하는 마지막 규칙은, 최소/최대 조건이다.

최소 힙 조건

모든 노드의 값은 그 자식 노드의 값들보다 작아야 한다.
(왼쪽 값, 오른쪽의 값 사이의 크기 관계는 상관없다.)
따라서, 트리 맨 위에 최소값이 온다.

최대 힙 조건

모든 노드의 값은 그 자식 노드의 값들보다 커야 한다.
따라서, 트리 맨 위에 최대값이 온다.

어렵지 않다.
그냥 위에 있는 녀석이 무조건 커야(혹은 작아야) 한다.

완전 이진 트리를 배열로 나타내되,
완전 이진 트리가 최소/최대 조건을 만족하는,

이런 자료구조를 '힙(heap)'이라고 한다!

완전 이진 트리 + 최소/최대 조건 = 힙

힙은 반쯤 정렬된 배열이다.
가장 앞이 최대이거나 최소인 건 맞지만,
트리의 같은 층에 해당하는 숫자끼리는 정렬이 되어있지 않기 때문이다.

하나 더, 힙이 표현하는 이진 트리의 높이는 얼마일까?

매 층마다 2배씩 숫자가 늘어나기 때문에,
n개의 숫자를 힙으로 표현하면 트리의 높이는 log n이 된다.

n개의 숫자를 가진 힙의 높이 = log n

힙 정렬 1. 정렬되지 않은 배열로 힙 만들기

이제 힙 정렬을 이해할 준비가 모두 끝났다.

힙 정렬은 크게 2가지 단계로 이뤄져있다.
1. 정렬되지 않은 숫자들로 힙을 만드는 부분.
2. 힙으로 정렬된 배열을 만드는 부분.

먼저 1번을 알아보자.

힙을 만들기 위해서는 먼저 정렬되지 않은 배열에서,
모든 값이 최소/최대 조건을 만족시키도록 해야 한다.

예를 들어, i번째 노드가 최대 조건을 만족시키려면 어떻게 해야할까?

i번째 노드의 값과 자식 노드의 값을 비교한다.

만약 자식 노드 중에 더 큰 값이 있다면, i번째 노드와 그 자식 노드의 위치를 바꿔준다.

간단하다.

이 과정을 '힙으로 바꾸기(heapify)'라고 부른다.

하지만 완전히 랜덤하게 섞여있는 배열이기 때문에,
새롭게 바뀐 자식 노드도 최대 조건을 만족시키지 않을 수 있다.

그럼 그 자식 노드에 대해서도 똑같이 힙으로 바꿔준다.

(출처: programiz)

이 그림에서는,

부모인 2보다 자식인 10이 크다. 2와 10을 바꿔준다.
아래로 내려간 2보다 자식인 6이 크다. 2와 6을 바꿔준다.

이런 식으로 맨 아래층까지 모두 힙으로 바꿔주면,
마침내 우리는 전체가 모두 최대 조건을 만족하는 힙을 만들게 된다.

숫자 추가하기

만약 힙에 숫자를 새로 추가해야한다면 어떨까?

배열의 가장 마지막에 숫자를 추가해준다.
다시 모든 숫자에 대해서 '힙으로 바꾸기(heapify)'를 다시 해주면 된다.

힙 정렬 2. 힙으로 정렬된 배열 만들기

이제 힙을 정렬된 배열로 만드는 작업이다.

최대 힙을 기준으로 설명해보자.

최대 힙에서는 맨 위의 숫자가 가장 큰 숫자다.
최대값을 알고 싶다면 그냥 맨 위의 숫자를 반환하면 된다.

정렬된 배열이 필요하다면,
최대값을 계속 반복해서 뽑아주면 된다.

마치 휴지를 뽑아서 쌓는 느낌이랄까?

실제로는 절차는 어떻게 될까.

1. 힙의 맨 앞 숫자와, 힙의 맨 뒤 숫자를 바꿔준다.
맨 뒤에 있던 숫자가 갑자기 맨 앞으로 올라왔으니,
최대 조건이 깨졌을 것이다.

2. 이제 마지막 숫자는 힙의 범위에서 제외한다.
가장 큰 숫자를 맨 뒤로 보냈으니 정렬이 완료됐기 때문이다.

3. 범위 내에서 다시 '힙으로 만들기'를 반복한다.
모든 숫자는 규칙에 맞는 제자리로 가게 된다.

4. 다시 최대값을 맨 뒤로 보낸다.
힙으로 만들기를 반복해준다.

이 과정을 계속한다. 최대값들이 차례차례 배열의 뒷자리에 쌓인다.
n번 반복하면, 오름차순으로 정렬된다.

역시나 구체적인 코드까지 설명하는 글은 아니기 때문에,
자세한 구현 코드는 이 링크나 이 링크를 참조하자.

힙 정렬의 장단점

안정적인 성능

하나의 노드를 삽입하거나 삭제했을 때 힙 규칙을 유지하도록 바꾸는 작업은 O(log n)이다. 이진 트리의 높이만큼 반복하기 때문이다.

힙 정렬은 최악의 경우 n개 숫자를 삽입/삭제해야한다.
따라서 힙 정렬의 시간 복잡도는 O(n log n)이다.

힙 정렬은 최악의 경우에도 O(n log n) 연산으로 정렬을 완료하는 안정성을 보여준다.

추가 공간 필요 없음

힙 정렬은 배열 안에서 계속 요소의 위치를 바꾸는 식으로 힙 구조를 유지한다.
추가적인 공간이 필요하지 않다.

일부분만 필요할 때 좋음

전체 숫자 중에서 가장 작은 숫자 k개를 구해라.
힙 정렬은 이런 문제에 사용하기 좋다.

전체 숫자를 정렬하지 않고, 가장 작은 k개의 값만 구해야 한다면
힙을 재정비하는 연산을 n번 하지 않아도 되기 때문이다.

평균적으로 퀵 정렬보다 조금 느림

힙 정렬과 퀵 정렬은 모두 O(n log n)을 가진다.

그러나 힙 정렬의 경우 퀵 정렬보다 '캐시' 활용도가 떨어지기 때문에,
실제로 돌려보면 평균적으로 약간 더 느리다고 한다.

자료구조와 알고리즘

힙 정렬을 보면서, 적절한 자료구조에 적절한 알고리즘이 더해지면 우리가 원하는 작업을 굉장히 효율적으로 할 수 있다는 걸 실감했다.

물론 100% 완벽한 자료구조는 없다.
자료 구조는 특정한 상황에서 특정한 작업을 하는데 특화돼있다.

우리가 전화번호를 몰라도 이름으로 전화를 걸고 싶다면?
사진을 편집하다가 뒤로 가기 / 앞으로 가기를 하고 싶다면?
주어진 단어들을 알파벳 순으로 빠르게 정렬해야 한다면?

이런 구체적인 문제 해결 상황에 맞춰서
가장 좋은 자료구조와, 가장 좋은 알고리즘이 달라진다.

그리고 여태까지 오랜 시간 동안 프로그래밍을 해온 사람들이
'이런 문제를 해결하는 프로그램은 이런 식으로 자료구조/알고리즘을 쓰면 좋더라'하는 노하우를 우리는 알고리즘과 자료구조라는 이름으로 배운다.

힙 정렬을 공부하면서 왜 자료구조와 알고리즘이 항상 같이 언급되는지.
왜 이 둘을 잘 알아야만 하는지에 대해서 더 이해가 되는 느낌이다.

요약 정리

프로그래밍에서 자료구조란 데이터에 일정한 체계를 부여해서 정리하는 방법이다.
힙 정렬은 힙이라는 자료구조를 사용해서 효과적으로 정렬 문제를 해결한다.
힙은 최소/최대 조건을 지키는 완전 이진 트리 배열이다.
정렬되지 않은 배열에 '힙으로 바꾸기(heapify)'를 반복하면 힙이 된다.
힙에서 최대/최소값을 뽑아내면 정렬된 배열을 만들 수 있다.
힙 정렬은 최악의 경우에도 안정적이고, 추가 공간이 필요없다. 일부분만 구할 때 유용하다. 다만 실제 시간은 퀵 정렬보다 조금 느린 경향이 있다.
해결해야하는 문제에 따라, 자료구조/알고리즘의 장점과 단점을 잘 이해하고 사용하면 굉장한 효과를 발휘한다.