[Linear Algebra] Day 18. Solving a system of 3 equations and 4 variables using matrix row-echelon form

이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.
링크: Khan academy

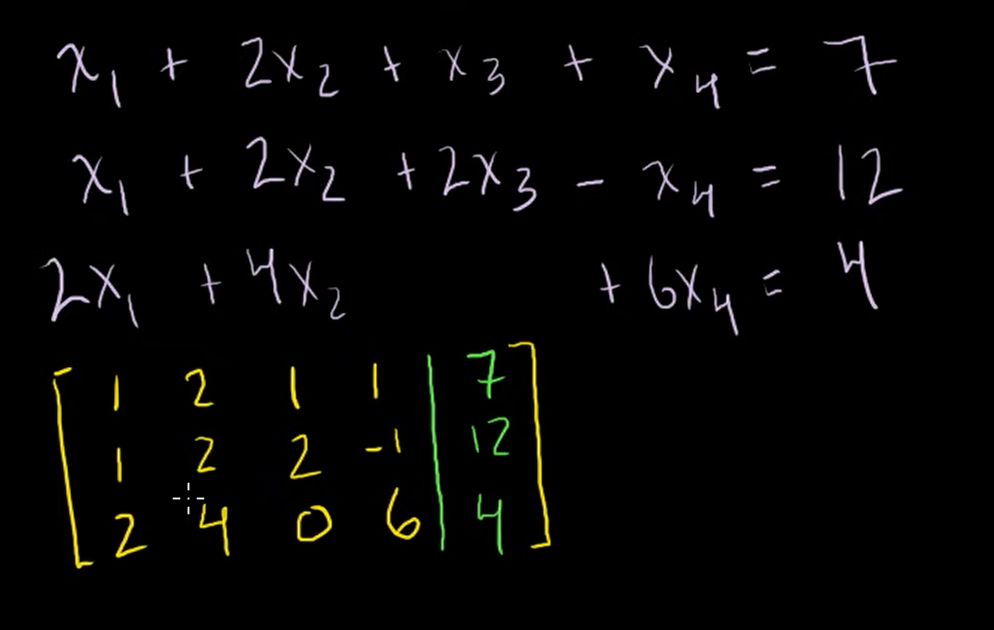미지수가 4개 있는 선형방정식을 풀기 위해 계수행렬을 만들어보자.

즉, 연랍방적식들의 계수행렬을 만드는 것인데, 선을 기준으로 오른쪽은 첨가행렬로 방정식들을 쓰는 다른 방법일 뿐이다.

이렇게 함으로써 스칼라 방정식처럼 곱하고 더하고 빼고 행렬 변환을 자유자재로 시킬 수 있다.

행렬을 다른 형태로 변환해보자.

어떤 행에서 계수 하나를 1로 만든 후 나머지 열들에 있는 값을 0으로 만들어보자. 이는 벡터의 선형독립 여부를 알아보기 위해 사용한 방식이다.

Reduced Row Echelon Form(REF, 기약행사다리꼴)

이러한 형태를 ref라고 하는데 ref(A)를 만들어보자.

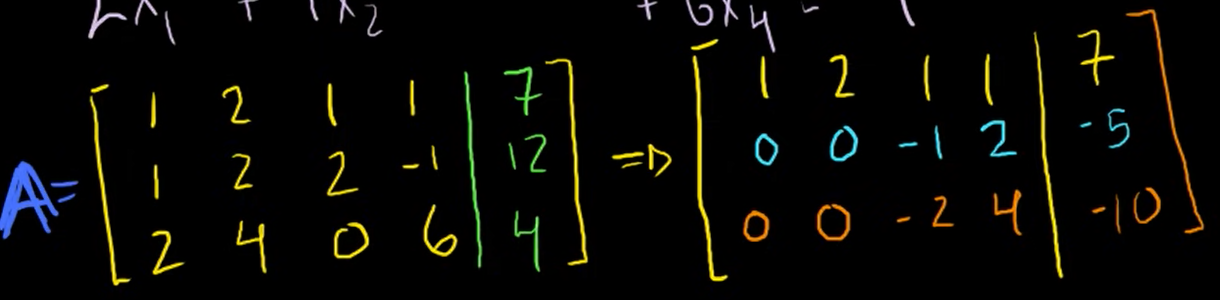
• 첫번째 행은 그대로 적어주고,
• 두번째 행은 첫번째 행에서 두번째 행을 빼준 값을 적는다.
• 세번째 행은 첫번째 행을 2배해준 뒤 뺀 값을 적는다.

2번째 행에서 선형계수 -1을 1로 바꾸기 위해 -1을 곱해주자.

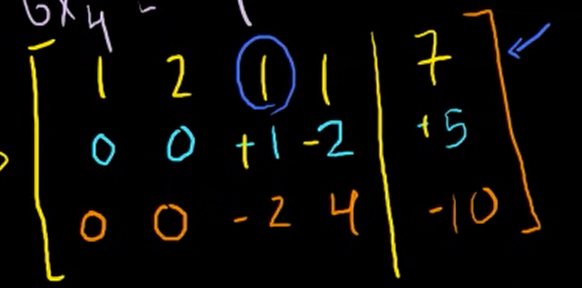2행을 기준으로 행렬을 정리하여,

3번째 행의 3번째 열에 있는 -2를 없애주기 위해 두번째 행을 2배한 값과 더해보자.

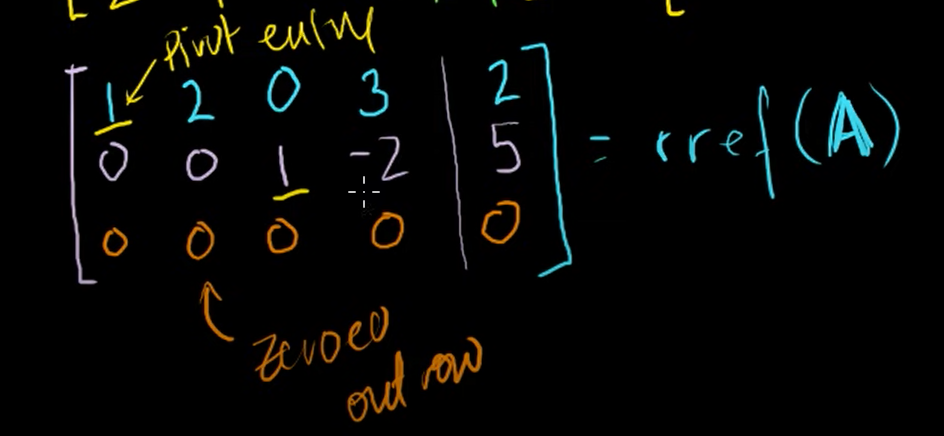이번엔 첫번째 행, 세번째 열에 있는 1을 0으로 만들어보자.

첫번째 행에서 두번째 행을 뺀 값을 적어보면, 기약행 사다리꼴이 만들어진다.

🎵 기약행 사다리꼴인 이유?

• 각 행의 선형계수(선행성분)가 1이며, 각 열에서 유일하게 0이 아닌 수이다.
  이는 pivot entry(피벗 성분)이라고 부른다.
• Zeroed out row(0으로 된 행)은 기약행 사다리꼴에서 마지막 행이된다.

원래의 선형방정식으로 돌아가서,

계수들을 기약행 사다리꼴을 이용하여 연립방정식을 간단하게 다시 써보자.

여기서 $x_1, x_3$와 같이 피벗 성분과 관련된 변수를 Pivot variable(피벗변수)라고 한다. 그리고 Pivot entry와 관련된 나머지 변수들인 $x_2, x_4$를 free variable(자유변수)이라고 한다.

미지수보다 식이 적을 때 해가 많기 때문에, free variable은 어떤 변수로든 set(결정)할 수 있다.

자유변수를 구하기 위해 식을 정리해보자.

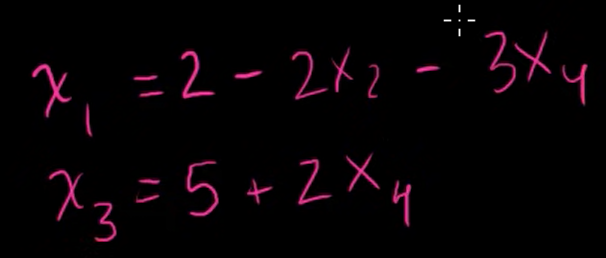
좀 더 나은 시각화를 위해 식을 다르게 적어보자.

이 식에서 나올 해들을 벡터 $x_1, x_2, x_3, x_4$ 라고 하자.

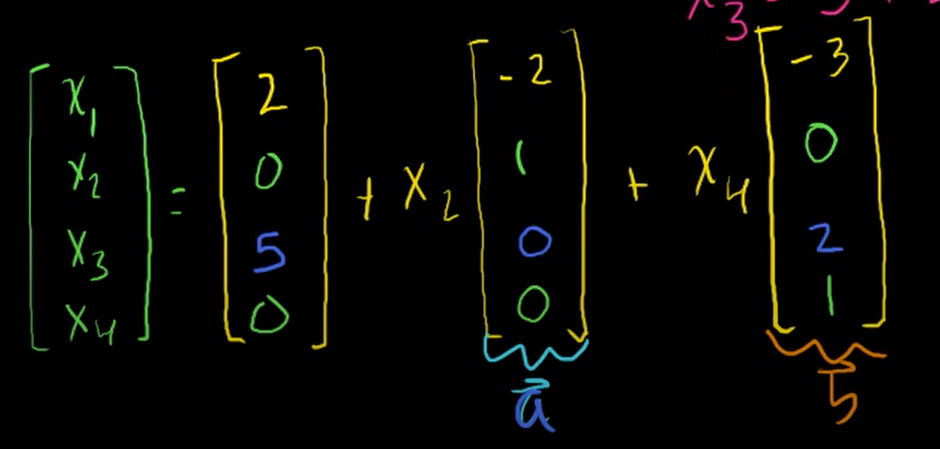
• solution set(해 집합)를 세 벡터의 linear combination(선형결합)으로 나타낼 수 있음을 볼 수 있다.
• 해 집합은 $R^4$안에 있는 위치 벡터이다.

$R^3$에서의 위치 벡터 하나를 가정해보자. -> 왜 $R^3$에서 가정??? 이해를 돕기 위함 ^^

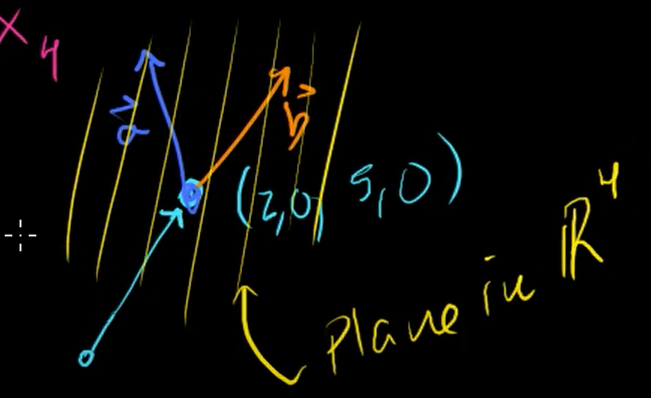원점에서부터 시작하는 벡터 (2, 0, 5, 0)는 두 벡터 $\overrightarrow{a}$, $\overrightarrow{b}$의 배수들을 더한 것과 같다.

그렇다면, $R^4$내에서 해집합은 고정되어 있는 위치 벡터(fixed point)와 $\overrightarrow{a}$와 $\overrightarrow{b}$의 선형결합의 합과 같다는 것을 알 수 있다.

즉, $\overrightarrow{a}$, $\overrightarrow{b}$의 선형결합은 점 (2, 0, 5, 0)을 포함한 평면이 된다.

🎵 미지수보다 식이 적으면 해가 제한되지 않는다는 성질을 기억하자.

4가지 미지수를 가진 3개 방정식의 해 집합은 $R^4$상의 평면으로 표현할 수 있다는 결론을 얻었다.