[Linear Algebra] Day 21. Matrix vector products

이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.
링크: Khan academy

행렬과 벡터의 곱에 대해 알아보자.

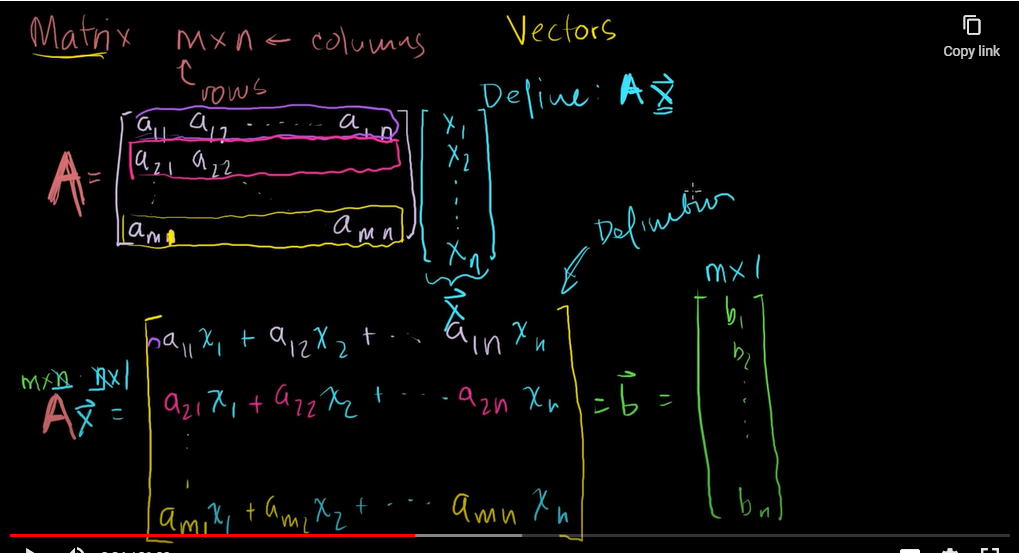
$A = m \times n$와 $\overrightarrow{x} = \begin{bmatrix}x_1\\x_2\\\vdots\\x_n \end{bmatrix}$

행렬 A를 $\overrightarrow{x}$와 곱해보자.

이 때, 열벡터 x의 개수가 행렬 A의 열의 개수와 같아야지만 연산이 가능하다.

$A\overrightarrow{x}$를 풀어쓰면 $\overrightarrow{b}$로 나타낼 수 있다.

그렇다면 $\overrightarrow{b}$의 entry(항목)은 몇개일까?

• 행렬 A에 있는 각 행벡터와 열벡터 x를 내적하는 것과 같다.
• 행렬 A의 첫번째 성분 곱하기 벡터 x의 첫번째 성분 ... and so on.

여기서 $A$의 크기는 $m \times n$이고, $\overrightarrow{x}$의 크기는 $n \times 1$이므로 이 둘을 곱한다고 쓸 수 있다. 가운데 항목이 같으므로 없애주면 행렬 $A\overrightarrow{x}$ = $\overrightarrow{b}$의 크기는 $m \times 1$이 된다.

• 행렬의 곱셈이 가능하려면, 가운데 두 항이 같아야 한다.

실제 숫자를 적용한 예시로 넘어가보자.

크기가 $2 \times 4$인 행렬과 $4 \times 1$인 행렬을 곱해보자.

첫번째 matrix의 행 각각을 행벡터로 보았을 때, 연산의 결과는 첫번째 행벡터와 두번째 열벡터의 내적이 된다.

앞서 언급했듯이 $2 \times 4$ 행렬의 행 각각을 행벡터로 본다면,
이를 $\overrightarrow{a_1}$, $\overrightarrow{a_2}$의 전치행렬로 나타낼 수 있게 된다.

즉, $\begin{bmatrix}\overrightarrow{a_1}\top\\\overrightarrow{a_2}\top\end{bmatrix}$ $\overrightarrow{x}$ = $\begin{bmatrix}\overrightarrow{a_1}\cdot \overrightarrow{x}\\\overrightarrow{a_2}\cdot \overrightarrow{x}\end{bmatrix}$이므로

전치행렬과 $\overrightarrow{x}$의 내적은 열벡터끼리의 내적과 같음을 알 수 있다.

다음 예시는 행렬 A의 행벡터가 아닌 열벡터의 집합으로 생각해보자.
A벡터의 열벡터를 각각 $\overrightarrow{V_1}$, $\overrightarrow{V_2}$, $\overrightarrow{V_3}$, $\overrightarrow{V_4}$라고 하자.

이를 $\overrightarrow{x}$와 곱해주면 위와 같은 식이 나온다.
강의에서 "the matrix X dictates the weights on each of the columns are."라고 설명 되어 있으므로, $\overrightarrow{x}$가 가중치 행렬이 된다.

이 식을 통해, 행렬 A의 열벡터들의 선형조합으로 나타낼 수 있음을 알 수 있다.

= linear combination of column vectors of A

오늘은 늦잠을 자지 않은 기념으로 스터디 인증샷 ,, ,ㅎ