이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.
링크: Khan academy

More on linear independence

S는 서로 선형 종속 관계인 벡터들의 집합이다.

선형 종속 관계에서는 "one vector can be represented by the combination of the other vectors"라고 지난 강의에서 정의하였다.

집합 S는 필요충분조건으로 $c_1v_1$ + $c_2v_2$ + $...$ $c_nv_n$ = 0 = $\begin{bmatrix}0\\...\\0 \end{bmatrix}$을 만족시킨다.

🍊 if and only if(iff) = 필요충분조건

출처: https://article2.tistory.com/1346 !

즉, 선형 종속이라는 조건을 만족하기 위해서는 오른변에 있는 식이 성립해야 한다는 것이다.

여기서, $c_i$중에 적어도 하나는 0이 아니라는 점에 주목하자.

다른 말로하자면, 벡터 하나를 다른 벡터들의 합으로 표현할 수 있다는 것이다.

• $v_1$ = $a_2v_2$ + $a_3v_3$ + $...$ $a_nv_n$

양변에 v1을 빼주어 왼변을 = 0으로 만들면,
보시다시피 적어도 constant 하나는 -1이기 때문에 0이 아니라는 조건을 만족한다.

이번엔 오른변에 있는 조건이 참이라고 가정하였을 때 왼변이 참이되는 것을 증명해보자.

여기서 $v_1$를 다른 벡터들의 결합으로 표현해낼 수 있으므로,

선형 종속임을 증명할 수 있다.

• at least one of these constants is != 0,
• can represent vector v1 as some combination of the other vectors

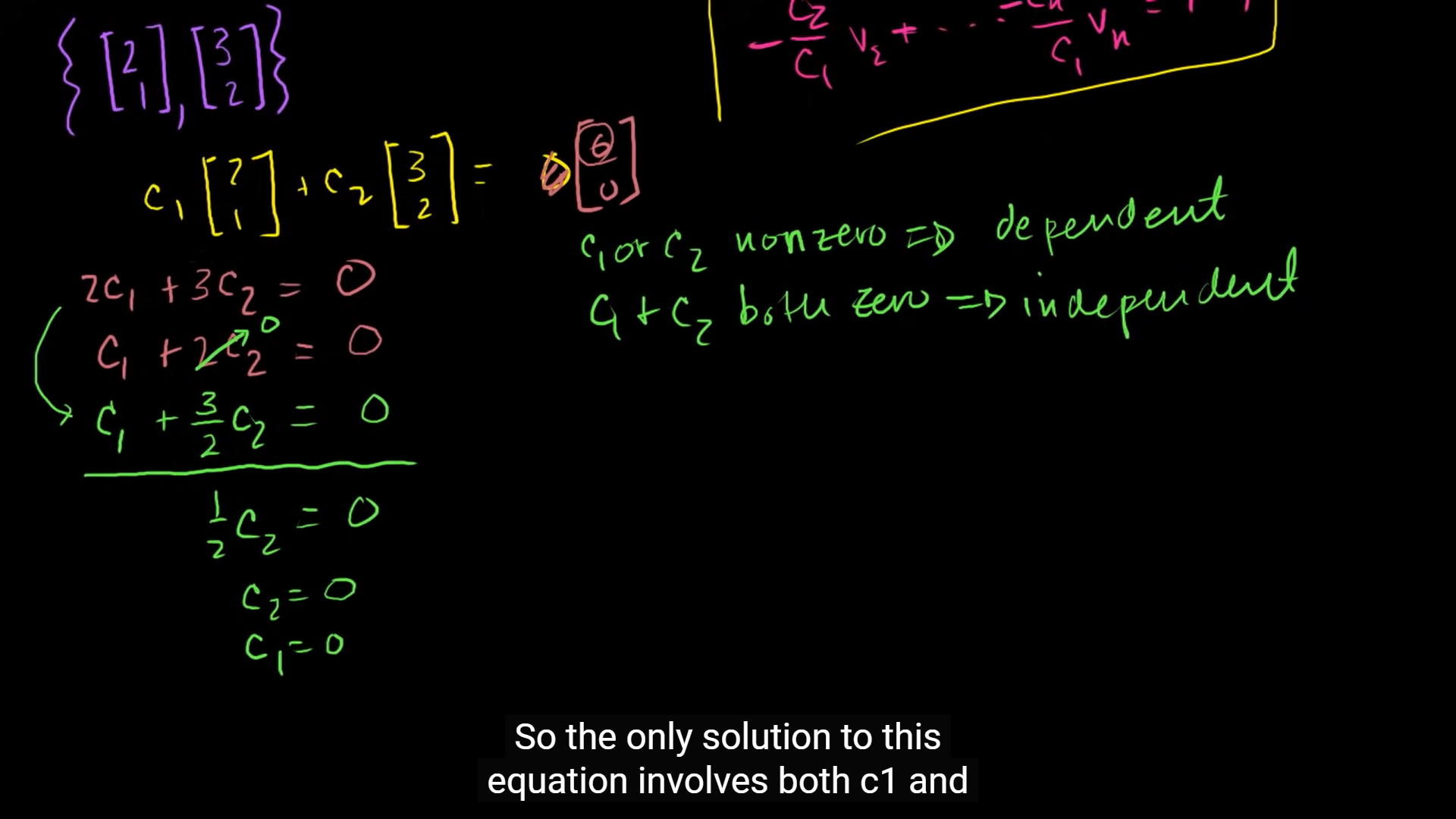
예시를 보자.

• $c_1$ 또는 $c_2$ 중 하나가 non zero => dependent
• 둘다 = 0 이어야만 식이 성립한다면 => linearly independent

둘다 0일 때만 식이 성립하기에 이는 선형 독립의 예시임을 알 수 있다.

🍊 정리하자면,

• neither of them are redundant of the other one.
• can't represent one as a combination of the other
• span R2

다음 예시를 보면, 3개의 2차원 벡터가 있다.
다른 말로 하면, "one of them is going to be redundant"하다는 뜻이다.
연립 방정식을 풀면 알 수 있겠지만 풀지 않아도 선형 종속 관계에 있음을 알 수 있다.

🍊 여기서 주목할 점,
저 3개중에 하나만 콕 찝어서 redundant하다고 할 수 없고, 어떤거든 그럴 수 있다는 점이다.

Span and linear independence example

이전 강의들에서 다룬 내용을 총체적으로 설명한 예시이다.

• linearly independent set of vectors
• none of these vectors can be represented as the combination of the other two
  
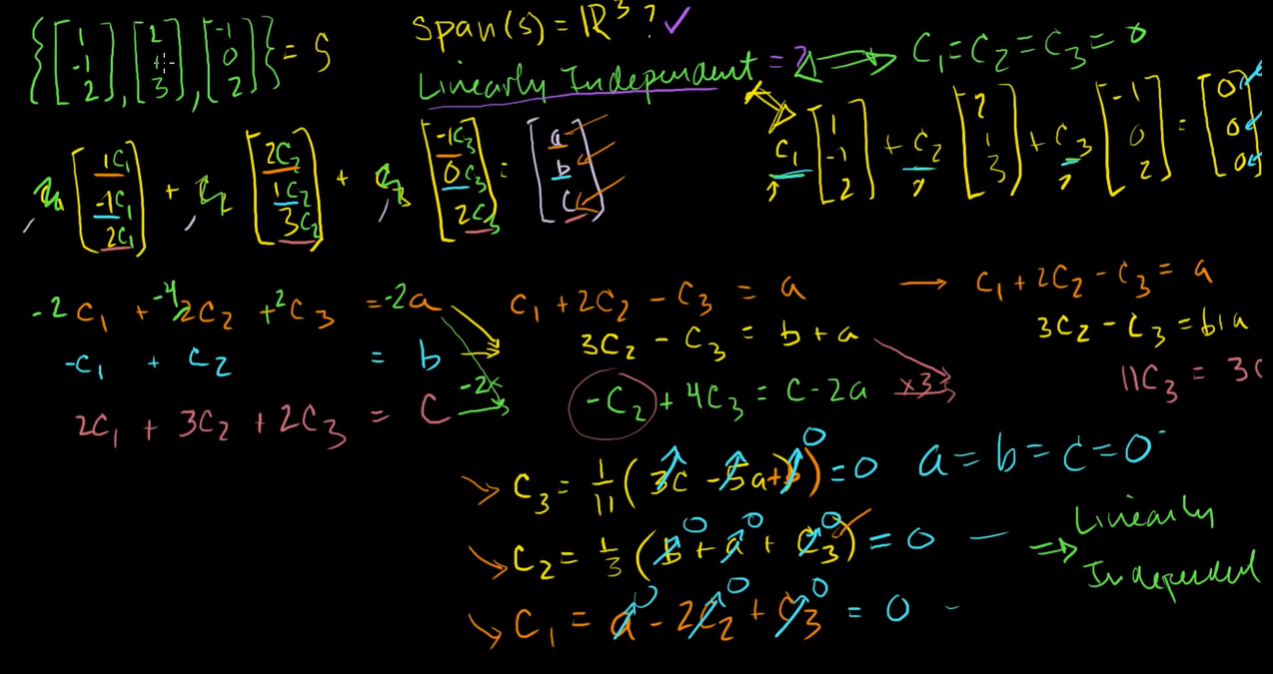
• each of these is contributing new directionality,
• they're not completely orthogonal to each other but,
• they're giving just enough directionality to add a new dimension

이미 알고 있는 내용이라 간단히만 정리해보았다.