[Linear algebra] Day 4. Introduction to linear independence

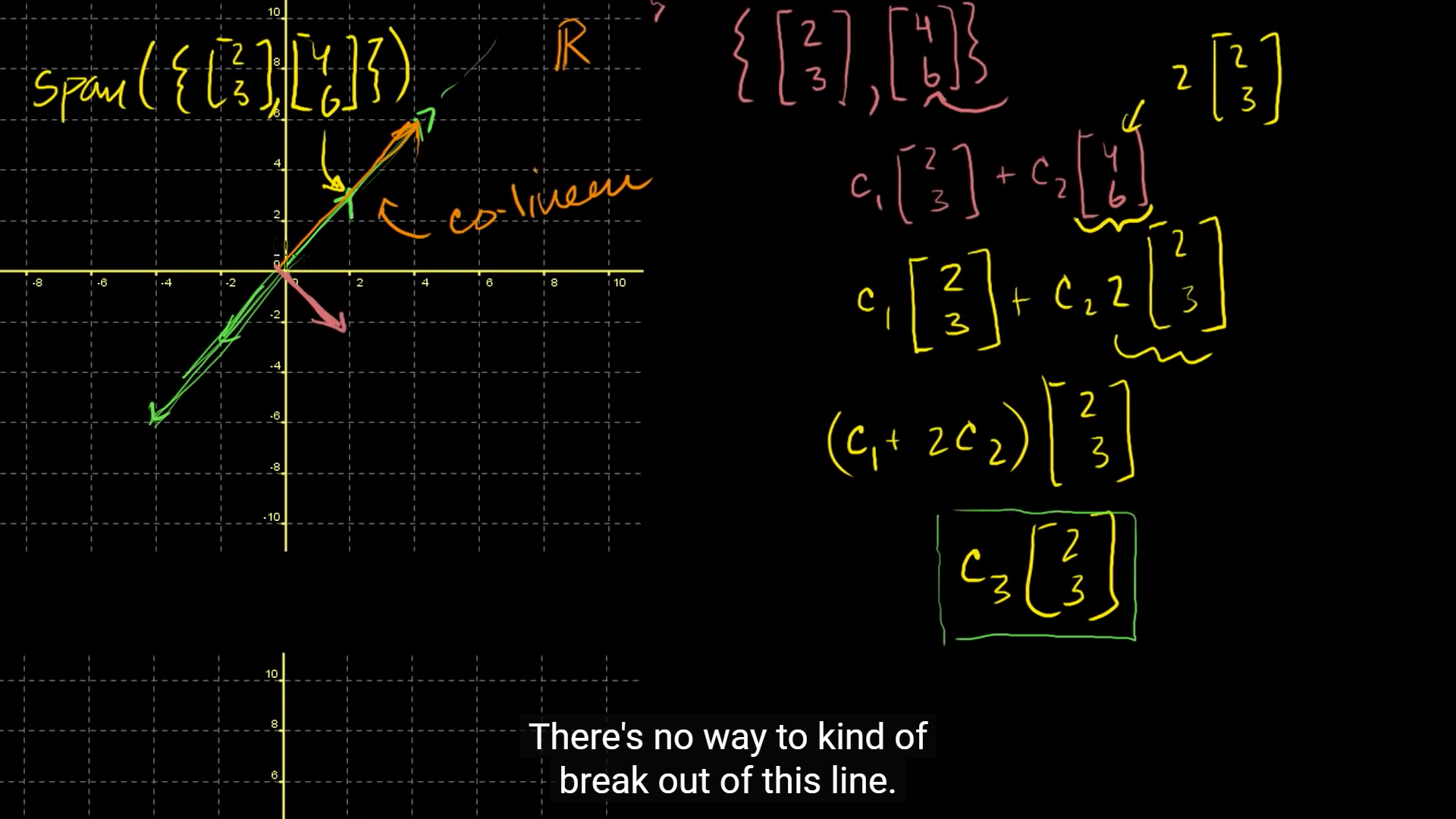
이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.
링크: Khan academy

이번 강의에서는 '선형 독립성'에 대한 내용을 다룬다.
만일 두 개의 vector 중 하나가 첫번째 vector의 스칼라(arbitrary constant)만큼 곱해져 있는 관계를 갖는다면, 위 처럼 표현할 수 있다.

즉, $\begin{bmatrix}2\\3\\ \end{bmatrix}$은 2 *$\begin{bmatrix}2\\3\\ \end{bmatrix}$과 같으므로,

각각 $c_1$, $c_2$배 되어있는 벡터들을 결합한다고 했을 때,

($c_1$ + $2$$c_2$)$\begin{bmatrix}2\\3\\ \end{bmatrix}$이 된다.

여기서, ($c_1$ + $2$$c_2$)도 arbitrary constant(상수)일 뿐이니까 ($c_3$)$\begin{bmatrix}2\\3\\ \end{bmatrix}$으로 봐도 무방하다.

😋 linear combination of two vectors를 논하는 대신에 scalar combination of one vector처럼 한마디로 표현 할 수 있다는 점 !!

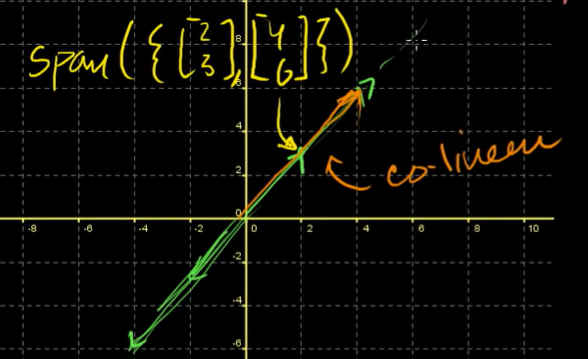
그래프에서 보면 알 수 있듯이, $\begin{bmatrix}2\\3\\ \end{bmatrix}$과 $\begin{bmatrix}4\\6\\ \end{bmatrix}$은 같은 직선이며 단지 두번째 벡터가 scale up이 되었다는 차이를 지니고 있을 뿐이다.

두 벡터의 span({$\begin{bmatrix}2\\3\\ \end{bmatrix}$, $\begin{bmatrix}4\\6\\ \end{bmatrix}$})은 위에서 보이는 직선이다.

😋 Span이 $R^2$ 전체가 아니라는 점에 주목하자.

즉, 두 벡터는 linearly dependent(선형 종속)인 것이다.

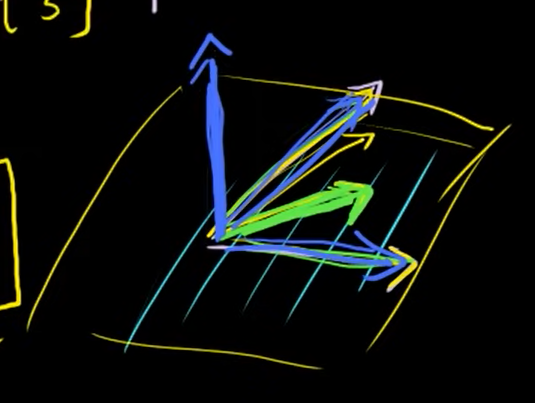3차원($R^3$)을 생각해보자.

위에서 보이는 초록색 직선은 같은 평면(coplanar)에 있는 두 개의 파란색 직선이 선형 결합한 결과이므로 linearly dependent하다고 할 수 있다.

다시 말해, 원래 있던 두개의 파란색 벡터의 span에 아무런 영향을 미치지 않는다는 뜻이다.

그렇다면, linearly independent하게 만드는 방법은 ?

2차원 평면에서 break out하여 두개의 파란 벡터의 span(영역) 바깥에 존재하는 벡터이면 된다.

😋 Span = 3차원($R^3$)이 되겠쬬?

예시 1.

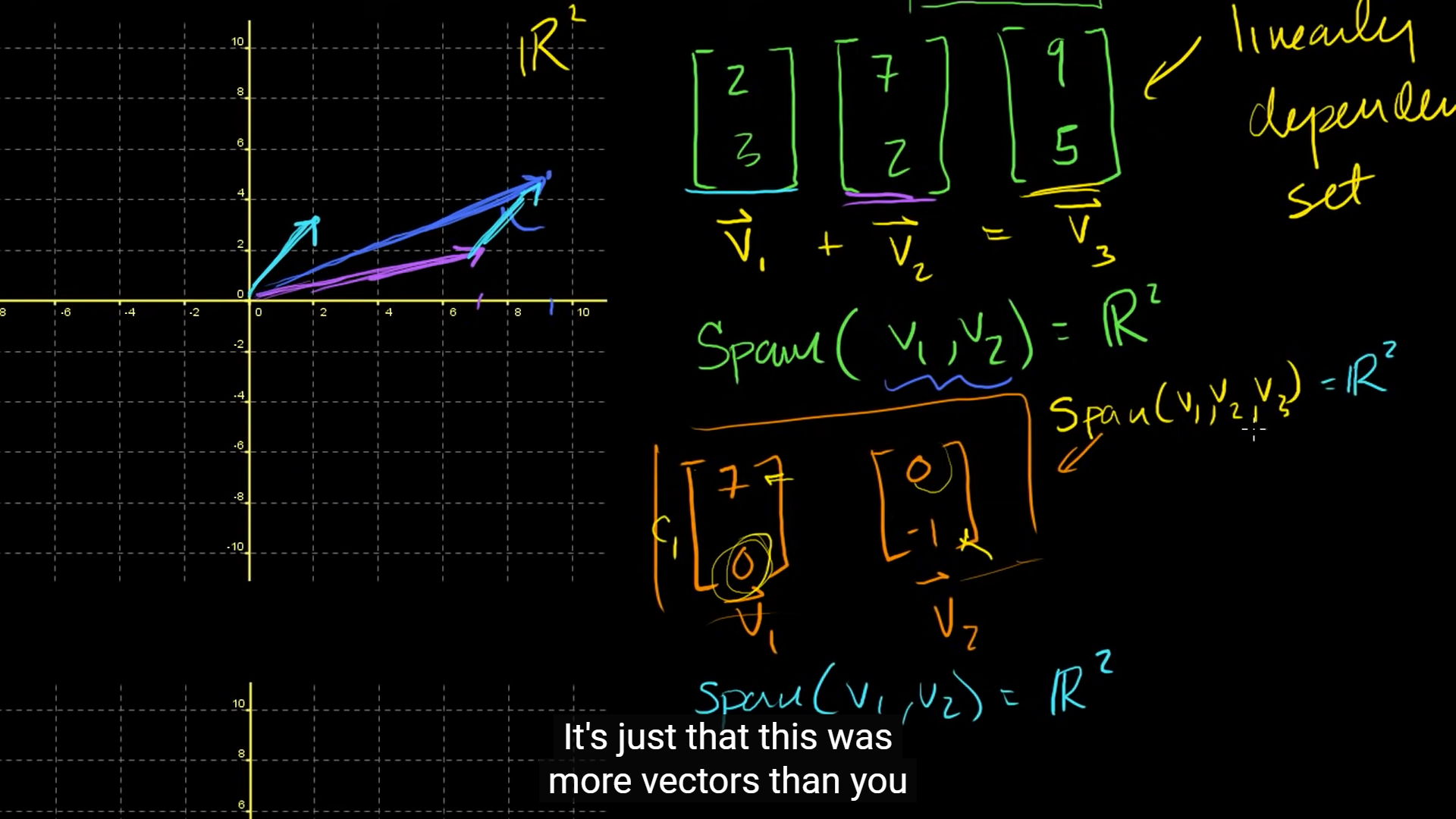
무관해 보이는 듯한 벡터들이지만 자세히 들여다보면 $\overrightarrow{V_1}$ + $\overrightarrow{V_2}$ = $\overrightarrow{V_3}$와 같은 관계를 가지고 있으므로, linearly dependent한 set이다.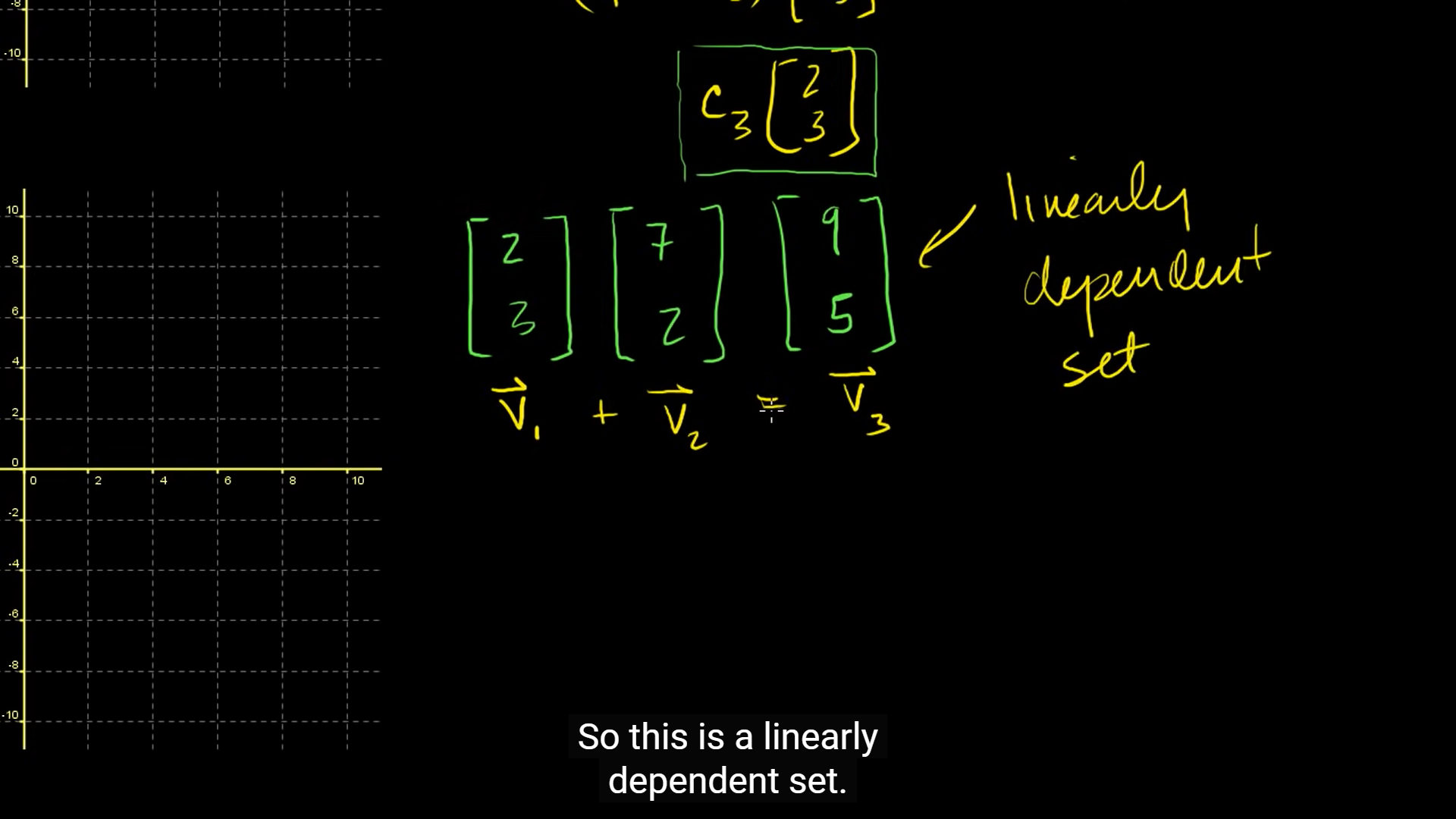

예시 2.

Span($\overrightarrow{V_1}$, $\overrightarrow{V_2}$, $\overrightarrow{V_3}$) = $R^2$이라는 표현은 상 당 히
redundant (not or no longer needed or useful; superfluous) 하다는 점.

😋 Linearly Independent (선형 독립)
= no way to represent one as a combination of the other

예시 3.

이 또한 linearly independent한 예시이다.
보시다시피, these three(3개의 벡터) do not lie on the same plane. 그리고 they're all adding new directionality.

• Span($\begin{bmatrix}2\\0\\0 \end{bmatrix}$, $\begin{bmatrix}0\\1\\0 \end{bmatrix}$, $\begin{bmatrix}0\\0\\7 \end{bmatrix}$) = $R^3$

아무리 살펴봐도 앞에 두개의 벡터의 linear combination으로 세번째 벡터를 나타낼 수 없다.

• 0과 0을 아무리 더하고 곱해봐도 7이 나올 수 없기 때문이다.
  

다음 강의에서는 더 많은 예시들과 함께 선형 독립에 대해 알아보도록 하자.