[Do it! 딥러닝] 3장 리뷰 - 선형회귀 뉴런

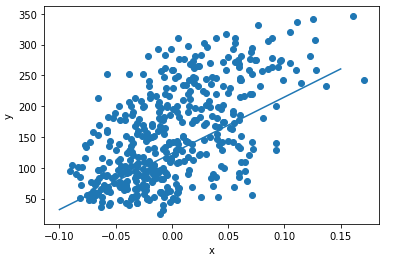
1. 사이킷런 당뇨병 환자 데이터 준비

import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()

plt.scatter(diabetes.data[:, 2], diabetes.target)
plt.xlabel('x')
plt.ylabel('y')
plt.show()

x축 : diabetes.data의 세 번째 특성
y축 : diabetes.target
x축과 y축의 정비례 관계

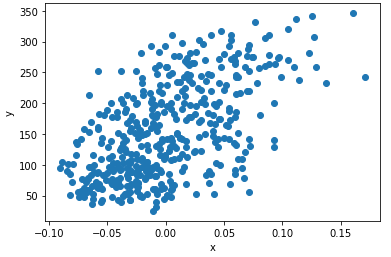
훈련데이터 준비

x = diabetes.data[:, 2]
y = diabetes.target

2. 경사하강법

모델이 데이터를 잘 표현할 수 있도록 기울기를 사용하여 모델을 조금씩 조정하는 최적화 알고리즘

훈련 데이터에 맞는 w와 b값 찾기

w = 1.0
b = 1.0

y_hat = x[0] * w + b

w_inc = w + 0.1
y_hat_inc = w_inc * x[0] + b

w_rate = (y_hat_inc - y_hat) / (w_inc - w)

w_new = w + w_rate

b_inc = b + 0.1
y_hat_inc = x[0] * w + b_inc

b_rate = (y_hat_inc - y_hat) / (b_inc - b)

b_new = b + 1

err = y[0] - y_hat
w_new = w + w_rate * err
b_new = b + 1 * err

y_hat = x[1] * w_new + b_new
err = y[1] - y_hat
w_rate = x[1]
w_new = w_new + w_rate * err
b_new = b_new + 1 * err

for x_i, y_i in zip(x, y):
    y_hat = x_i * w + b
    err = y_i - y_hat
    w_rate = x_i
    w = w + w_rate * err
    b = b + 1 * err

그래프 확인

plt.scatter(x, y)
pt1 = (-0.1, -0.1 * w + b)
pt2 = (0.15, 0.15 * w + b)
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
plt.xlabel('x')
plt.ylabel('y')
plt.show()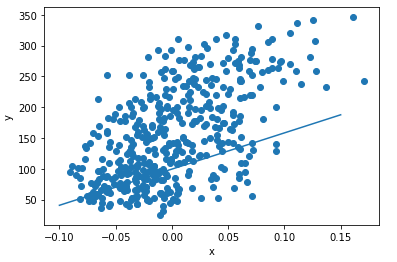

에포크 반복

for i in range(1, 100):
    for x_i, y_i in zip(x, y):
        y_hat = x_i * w + b
        err = y_i - y_hat
        w_rate = x_i
        w = w + w_rate * err
        b = b + 1 * err

plt.scatter(x, y)
pt1 = (-0.1, -0.1 * w + b)
pt2 = (0.15, 0.15 * w + b)
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
plt.xlabel('x')
plt.ylabel('y')
plt.show()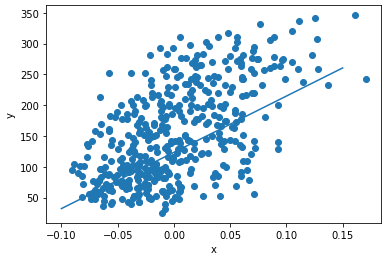

모델로 예측하기

x_new = 0.18
y_pred = x_new * w + b

plt.scatter(x, y)
plt.scatter(x_new, y_pred)
plt.xlabel('x')
plt.ylabel('y')
plt.show()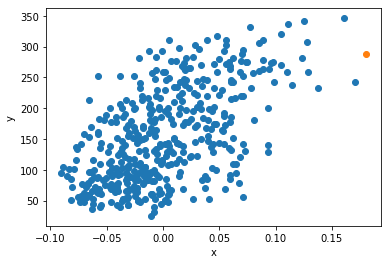

3. 선형회귀를 위한 뉴런 만들기

class Neuron:
    
    def __init__(self):
        self.w = 1.0     # 가중치를 초기화합니다
        self.b = 1.0     # 절편을 초기화합니다
    
    def forpass(self, x):
        y_hat = x * self.w + self.b       # 직선 방정식을 계산합니다
        return y_hat
    
    def backprop(self, x, err):
        w_grad = x * err    # 가중치에 대한 그래디언트를 계산합니다
        b_grad = 1 * err    # 절편에 대한 그래디언트를 계산합니다
        return w_grad, b_grad

    def fit(self, x, y, epochs=100):
        for i in range(epochs):           # 에포크만큼 반복합니다
            for x_i, y_i in zip(x, y):    # 모든 샘플에 대해 반복합니다
                y_hat = self.forpass(x_i) # 정방향 계산
                err = -(y_i - y_hat)      # 오차 계산
                w_grad, b_grad = self.backprop(x_i, err)  # 역방향 계산
                self.w -= w_grad          # 가중치 업데이트
                self.b -= b_grad          # 절편 업데이트

neuron = Neuron()
neuron.fit(x, y)

뉴런을 활용한 모델의 직선 그래프

plt.scatter(x, y)
pt1 = (-0.1, -0.1 * neuron.w + neuron.b)
pt2 = (0.15, 0.15 * neuron.w + neuron.b)
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
plt.xlabel('x')
plt.ylabel('y')
plt.show()