Transformer Summary

Previous RNN/CNN based models vs Transformer

• RNN/CNN based models connect encoder/decoder through attention mechanism (Previous)

Factor symbol position of input & output sequences
Parallization almost impossible
Cannot handle dependencies among long sequential input (linear/log increase of operations when trying to relate signals from distant two positions)

• Transformer (New)

Only based on "Attention Mechanism" (omitting RNN/CNN structure from model)
More paralizable (faster training & better quality)
Generalize well in other task (even in extreme cases "large/scarce data)

• One of the biggest difference
  Attention (not consider distance of I/O sequence) vs Self-Attention (Consider positions of single sequence when computing representation)

Model Architecture

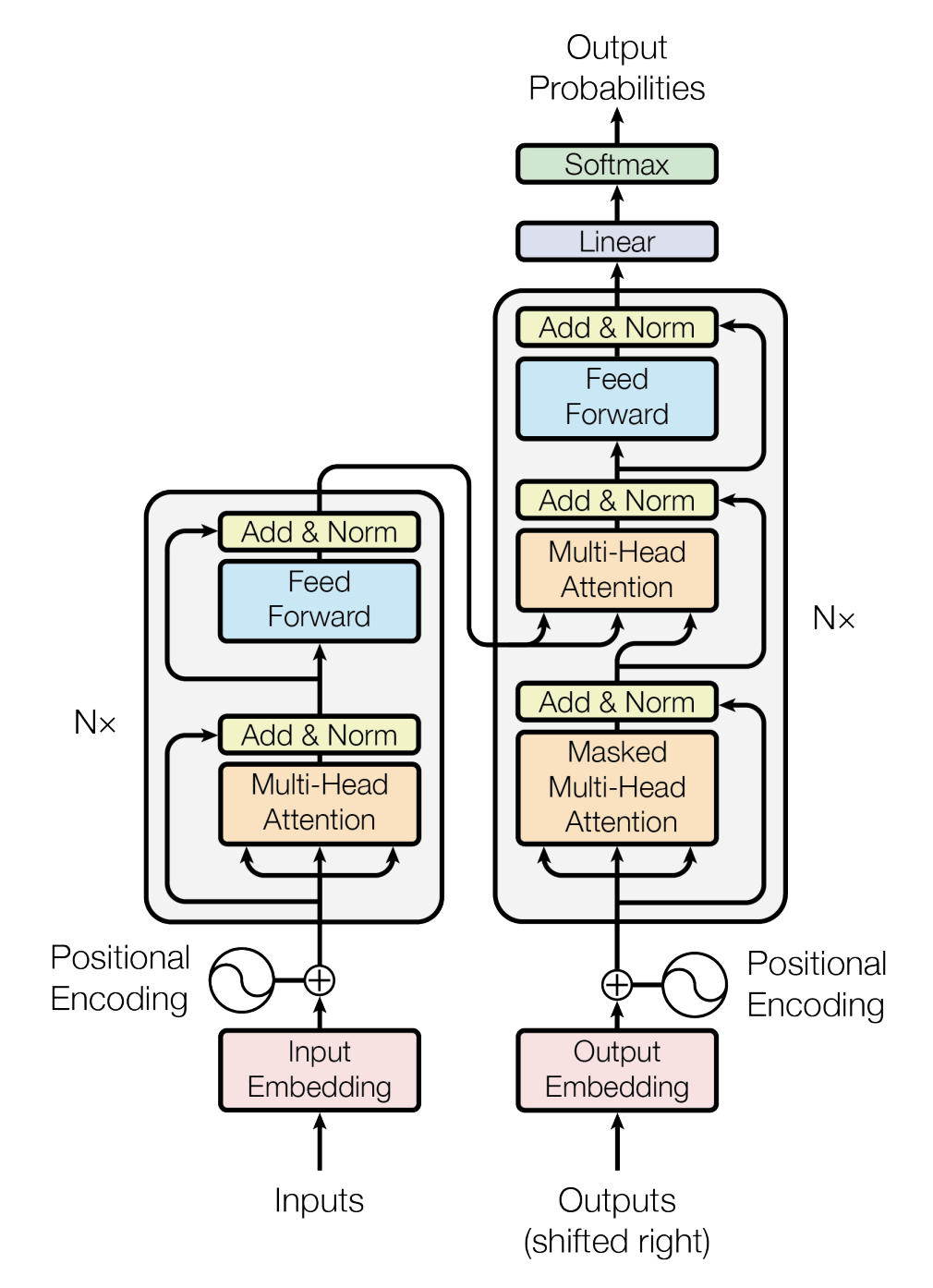
• Stacked self-attention and point-wise
• Fully connected layers for Encoder/Decoder

Encoder (left of the provided figure)

• Stack of 6 identical layer of the following

1 layer -> 2 sub-layer -> [multi-head self-attention mechanism] + [position wise fully connected FFN]

Each sub layer -> Residual Connection +
Normalization

Output:
LayerNorm(x + Sublayer(x))
Dimension: 512

• Sublayer(x) = function implemented by sublayer itself

Decoder (right of the provided figure)

• Stack of 6 identical layer of the following

1 layer -> 2 sub-layer (from above) + 1 sub-layer

Each sub layer -> Residual Connection +
Normalization

Plus one sublayer ->
-Masking added on self attention sub layer to prevent positions from attending to subsequent positions
-Ensure prediction for a position to only depend on known outputs of previous positions

Attention in Transformer (multi-head)

1. Encoder-Decoder Attention Layers
   Input: Q (query from decoder), K (memory keys) V (encoder output values)
   Serves purpose of encoder-decoder mechanism from 'previous' mainstream models

2. Self-Attention Layer in Encoder
   Input: K,V,Q (output of previous encoder layer)
   Each position in encoder can access all position from previous layer

3. Self-Attention Layer in Decoder
   Allow access of all previous positions within decoder (including current)
   Scaled Dot-Product attention implemented by masking input values of softmax to prevent "Leftward information flow"

---

What is Attention?
Attention Function map query and set of key-value pairs (vectors) to all outputs (vectors)
Output = Weighted Sum of Values

There are two methods calculating the weighted sum

1. Dot-Product Attention (used in Transformer)
2. Additive Attention
   -Dot-product attention tend to be much faster and space-efficient during performance
   -Possible to work with small values of dk (keys of dimension)
   -Additive approach performs better in case of large values of dk

Scaled Dot-Product Attention
Input: Q (Queries), dk (Keys of Dimesion), dv (Values of Dimension)

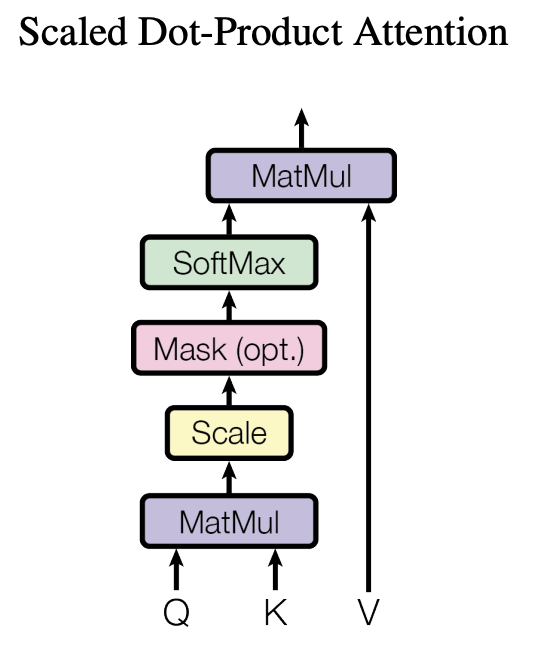
Attention(Q,K,V) =
Softmax(Dot_product(query, all_keys) / sqrt(dk))

Multi-Head Attention
Linearly projecting Q, K, V (h times) with different 'previously learned' linear projections to dk, dk, dv dimension

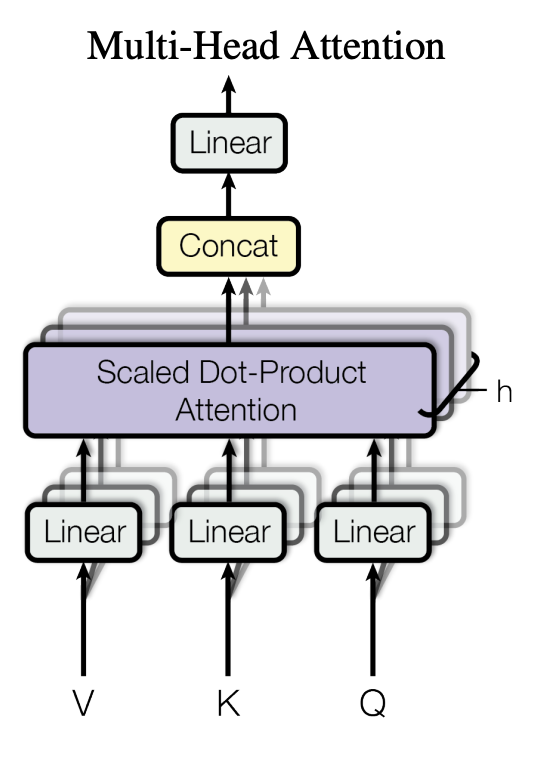
• Improvement over single-head:
  Allow model to gain access to information from differently represented subspaces at different positions

• Projected Q,K,V
  -> Allow attention function to perform in parallel manner
  -> Output = dv dimensional
  -> Each concatenated and re-projected
  -> return final values

Self-Attention
Connect all position with constant number of sequentially executed operations

Best performance when sequence length is smaller than representation dimensionality (which accounts for most of the case)

For improving performance on very long sequence, self-attention could be restricted to only consider certain neighborhood size on input sequence

Why Self-Attention was chosen for Transformer?

1. Total computational complexity per layer
2. Parallizable amount of computation
3. Shorter path between positional combination in input & output sequence, which allows long-range dependencies

---

Fully Connected Feed-Forward Network (inside each layer of encoder & decoder)

Made up of three parts

• 1 linear transoformation (xW1 + b1) = A
• ReLU Activation max(0, A) = B
• 1 linear transformation BW2 + b2

I/O Dimension = 512
Inner layer dimension (dff) = 2048

Embedding and Softmax

Usage of learned embedding

• convert I/O tokens to vectors

Learned linear transformation & softmax

• I: decoder output
• O: predicted next token probabilities

  Embedding weight matrix * sqrt(dmodel) == linear transformation matrix used right before softmax

Positional Encoding
Purpose:
Add positional encodings using sine and cosine functions of different frequencies to input embeddings at the bottom of the encoder and decoder stacks (to make up for not using Recurrence/Convolution)

Why use Sinusoid?
Sinusoid allow model to extrapolate to sequence length longer than 'other' versions that were tested (ex. linear)

Training Details

• WMT 2014 English-German Dataset (4.5 mil sentence pairs)
• 8 NVIDIA P100 GPU
• Optimizer: Adam
• Residual Dropout on output of each sub-layer