다중 회귀분석에서는 주어진 독립변수들로 종속변수를 잘 예측하는 회귀식을 구하기 위해 최소제곱법(Least Squares Method)을 사용
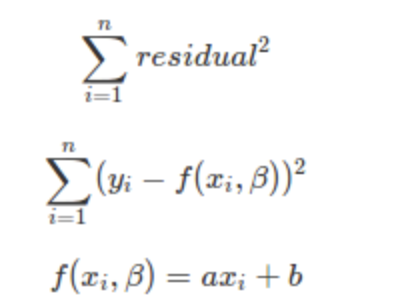
Residual 합의 최소값이 되는 a,b는 a 와 b 를 편미분하여서 도출
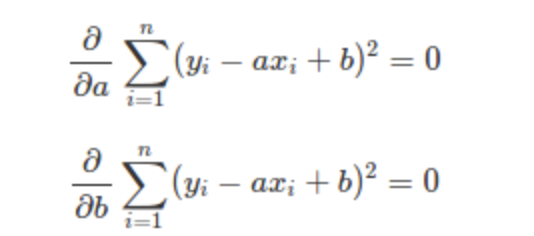
일반화선형모형(GLM), 로지스틱 회귀분석, Cox의 비례위험모형에서는 Maximum likelihood method (최대우도법)을 이용해서 회귀식을 추정
우도, 가능도 (Likelihood)
우도: 어떤 특정한 값을 관측할 때, 이 관측치가 어떠한 확률분포에서 나왔는가에 관한 값
확률(Probability) : 고정된 확률분포에서 어떠한 관측값이 나타나는지에 대한 확률
우도(가능도, Likelihood) : 고정된 관측값이 어떠한 확률분포에서 어느정도의 확률로 나타나는지에 대한 확률
Maximum likelihood method (최대우도법)
모수적인 데이터 밀도 추정 방법으로 파라미터로들로 구성된 어떤 확률밀도함수에서 관측된 표본 데이트들에서 파라미터들을 추정하는 방법
어떤 확률변수에서 표집한 값들을 토대로 하여 확률변수의 모수(parameter)를 구하는 것이 핵심!! 어떤 모수가 주어졌을 때, 원하는 값들이 나올 우도 (Likelihood)를 최대로 만드는 모수를 선택한다:)

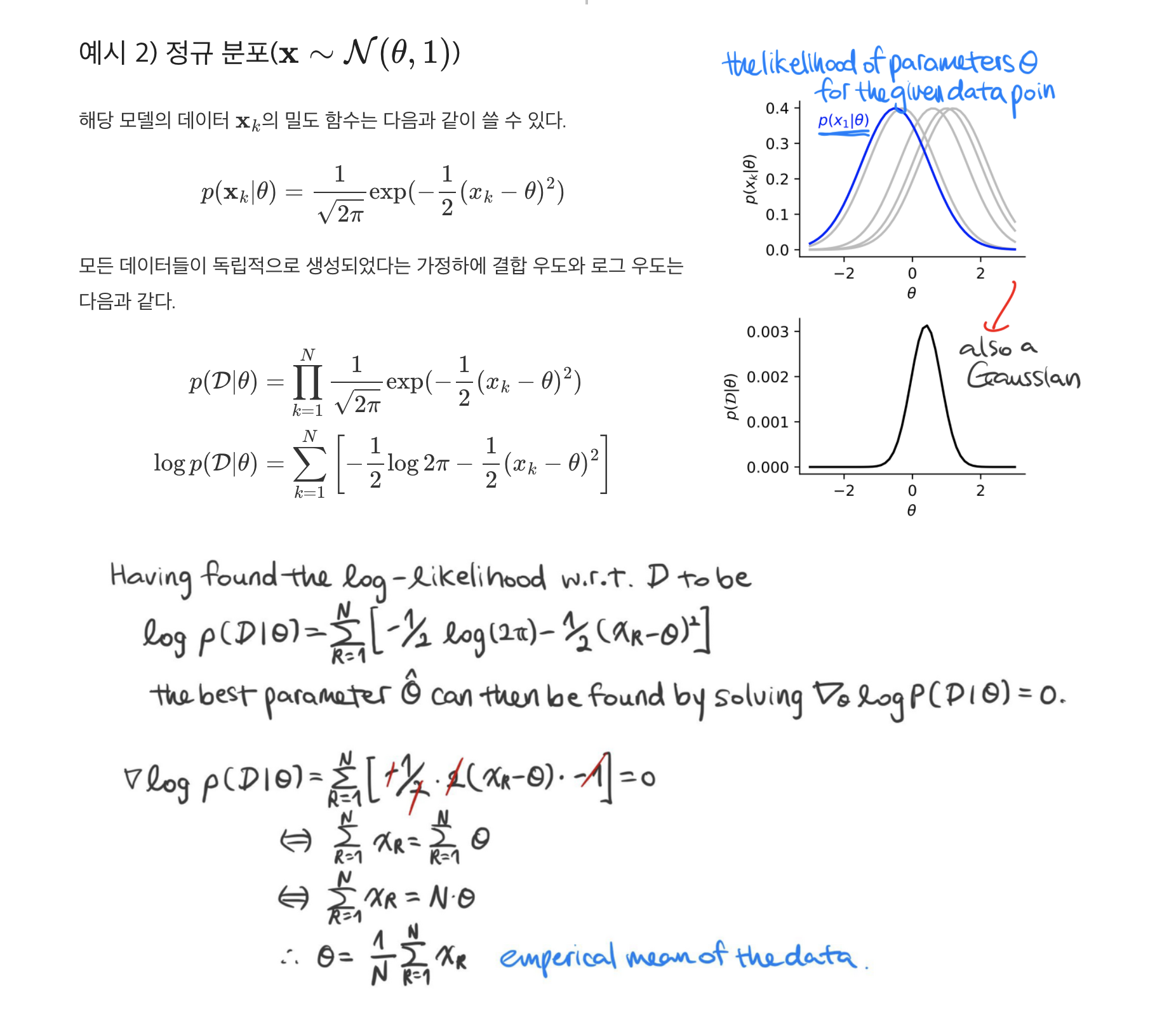
EX)
데이터를 관찰하여 이 데이터가 추출되었을 것으로 생각되는 분포의 특성을 추정가능-> 추출된 분포가 정규분포라고 가정하고, 분포의 특성 중 평균 추정
Likelihood function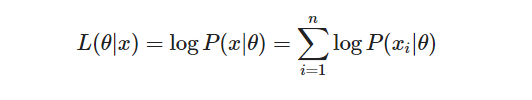
Likelihood(가능도)를 계산하는 방법:
각 데이터의 샘플에서 분포에 대한 높이(Likelihood 기여도)를 계산하여 모두 곱하는 형태
자연로그를 활용해 log-likelihood function을 이용한하면 계산이 좀더 편리한 이점을 갖는다:)
MLE는 Likelihood function의 최댓값을 찾는 방법으로 파라미터에 대하여 편미분해서 그 값이 0이 되도록 θ값을 찾는다
MLE의 예시로 표본 평균과 표본 분산을 이용하여 Likelihood function에서 모평균과 모분산의 추정도 가능함~
우도비 검정 (Likelihood ratio test)
-회귀모형에 변수를 하나 추가 또는 제거하면서 두 우동의 비를 통하여 회귀계수의 유의성을 검정하는 방법
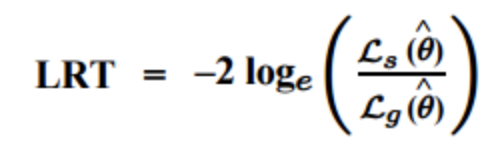
두개 모델의 우도비 비를 통해
우도비 검정 값: -2log(s모델의 우도/g모델의 우도)
자유도 1인 chi-squared 분포에 의하여 p-value를 계산하여 회귀계수의 유의성을 판단한다
References
https://www.statisticshowto.com/likelihood-ratio-tests/
https://angeloyeo.github.io/2020/07/17/MLE.html#%EC%B5%9C%EB%8C%80%EC%9A%B0%EB%8F%84%EB%B2%95%EC%9D%98-%EC%A0%95%EC%9D%98
https://minicokr.com/14
