Biostatistics
1.Biostatistics 통계 분석 Basic - (1)
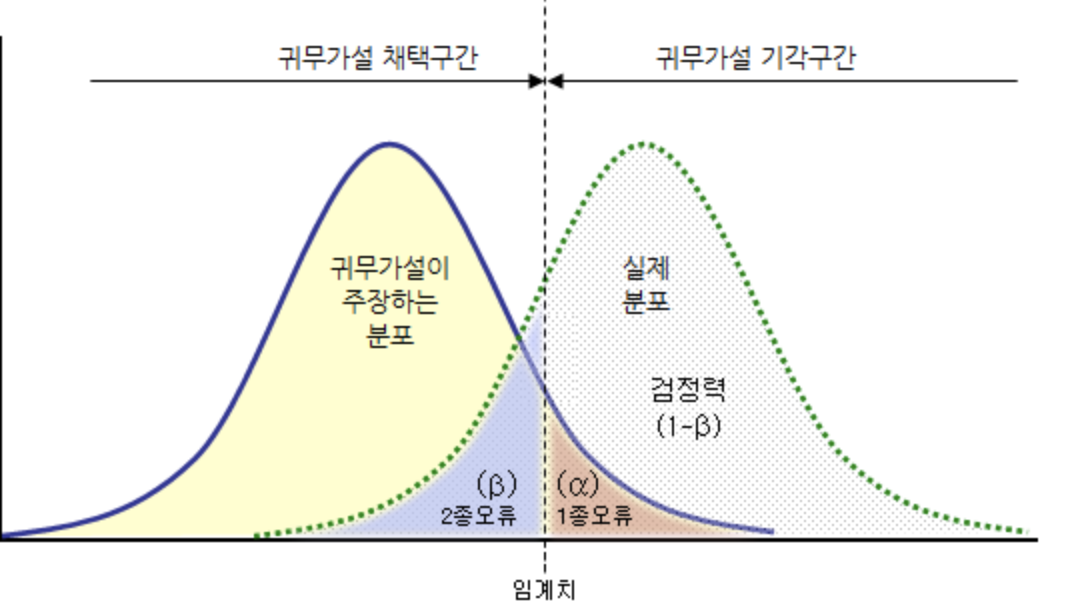
1종 오류: 실제로는 귀무가설이 참이나 기각한 경우 즉, 실제로는 평범하지만 특별하다고 판단한 경우 ^^;2종 오류 (Beta error): 실제로는 대립가설이 참이나 입증을 못하는 경우실제는 특별하지만 평범하다고 판단한 경우 EX) 효과가 없는 약의 경우 1종 오류에
2.Biostatistics 통계 분석 Flow-(a)

의학 통계에서 필요한 전체적 연구 통계 분석 flow를 정리해보겠습니다. 통계 분석에 활용할 수 있는 R코드도 조금이나마 간단하게 설명했습니다. 두 개 또는 그 이상의 집단을 무작위로 나눠서 집단이 동질하게 가정을 한 후에 주요 결과 변수에 관해 알아보는 방법입니다
3.Biostatistics 통계 분석 Flow-(b)
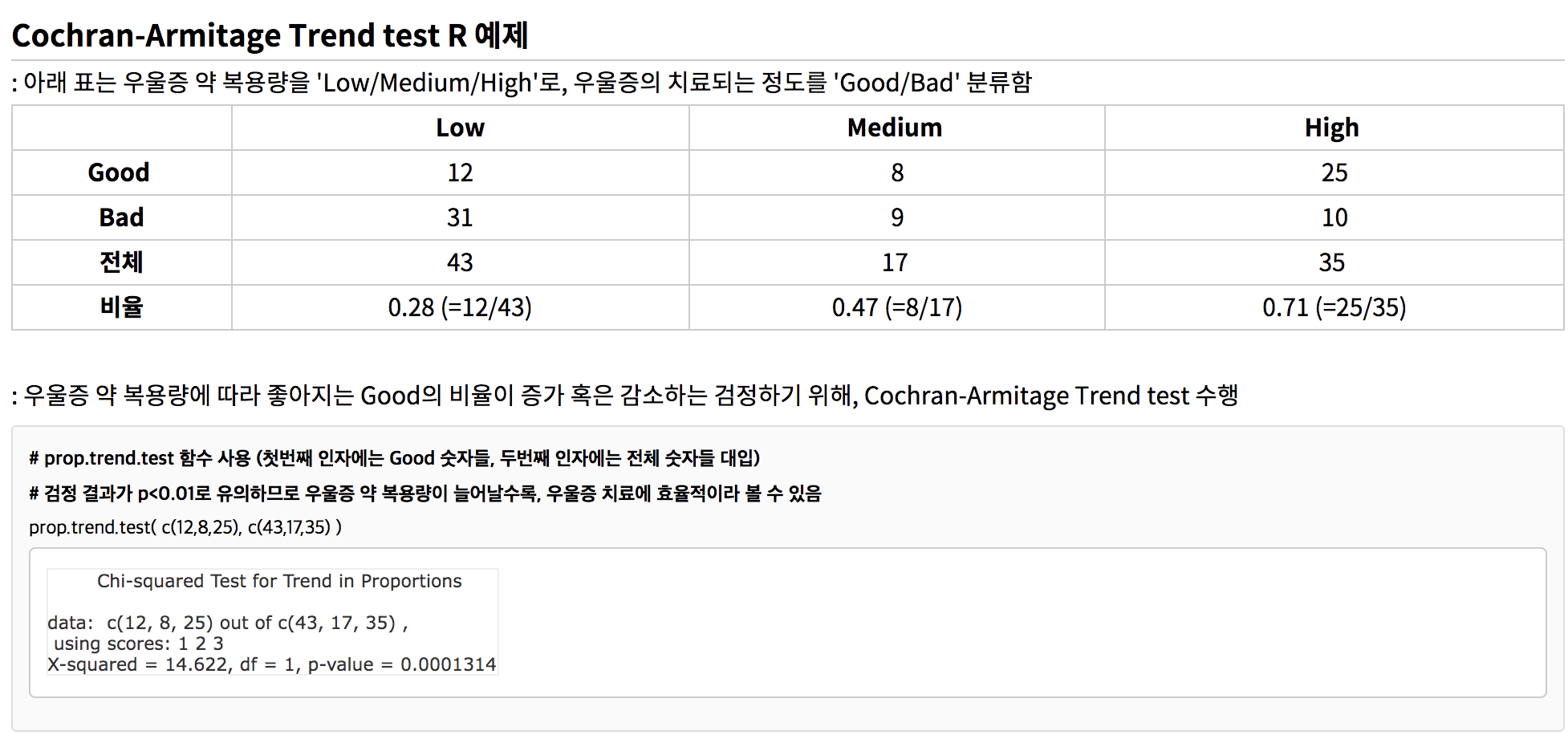
의학 통계에서 필요한 전체적 연구 통계 분석 flow를 저번 포스트에 이어 추가적으로 정리해보겠습니다.이번 편 역시 저번과 마찬가지로, 통계 분석에 활용할 수 있는 R코드도 조금이나마 간단하게 설명했습니다.짝을 이룬 자료의 비교 (paired data,repeated,
4.Biostatistics 통계 분석- Likelihood(우도)
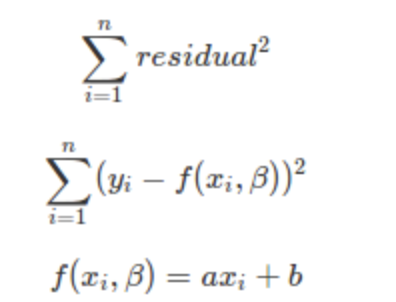
다중회귀분석에서는 주어진 독립변수들로 종속변수를 잘 예측하는 회귀식을 구하기 위해 최소제곱법(Least Squares Method)을 사용Residual 합의 최소값이 되는 a,b는 a 와 b 를 편미분하여서 도출일반화선형모형(GLM), 로지스틱 회귀분석, Cox의 비
5.Biostatistics 통계 분석- Bootstrapping (부트스트랩)
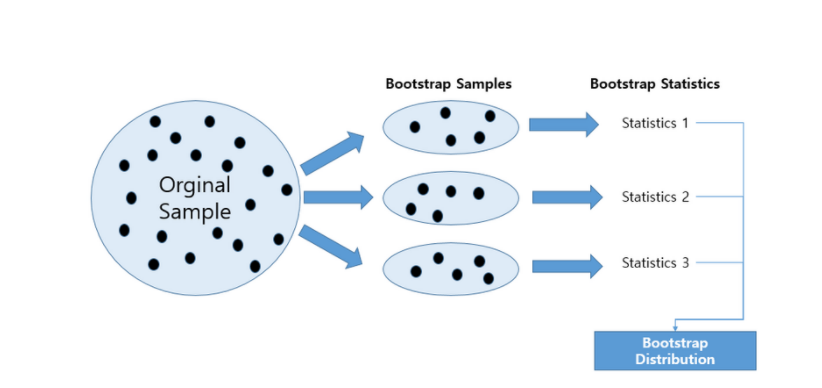
통계학에서의 bootstrap은 비모수 추정 방법으로 가설 검증을 하기 전에 random sampling을 적용하는 방법을 말합니다.예시를 들어보면 어떤 집단에서 값을 측정할 때, 임의로 100개를 뽑아 평균을 구하는 예가 있을 수 있습니다.측정된 n개의 표본 데이터
6.Biostatistics - ROC curve
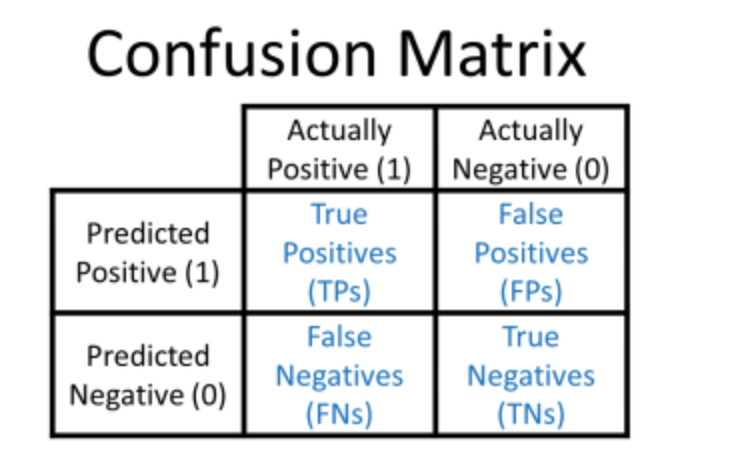
TP,FP,FN,TN 등 헷갈리는 경우가 있는 데 용어 개념 내용을 정리해보겠습니다. 앞에 나오는 True/Negative: 판단이 맞는 경우에는 TRUE, 판단이 다른 경우에는 NEGATIVEPositivie/Negative: 의사가 양성 진단하는 case (EX.
7.Biostatistics 통계 분석- 선형 회귀분석(Linear Regression)

Assumption of Regression -선형성 (Linearity): predictor(예측치)와 실제 값의 관계가 선형 plot(model)을 진행했을 때-> no fitted pattern 빨간 색 선이 0에 전체적으로 가까워야 함 -독립성 (Indepen
8.Biostatistics 통계 분석- 로지스틱 회귀분석 (Logistic Regression Analysis)
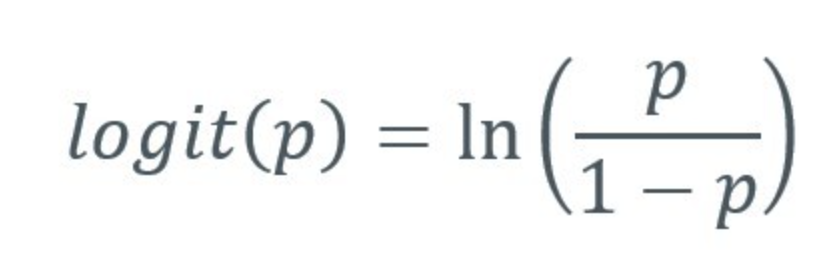
로지스틱 회귀분석: 특정 질병의 유무에 영향을 미치는 요인을 밝히는 통계 분석\-> 교란변수의 영향을 제거하고 여러 위험인자들이 관련되는 정도를 하나의 모형으로 설명 가능 Logit transformation을 통하여 < p는 각 수준에 따른 질병이 있을 확률,0
9.Biostatistics 통계 분석- 일반 선형 모델 GLM 확장 (General Linear model, Generalized Linear model, Generalized Estimating Equations)

\-결과 변수가 연속형 변수에 한정되어있고 정규 분포 가정을 따른다\-일반 선형 모형(General Linear Model)은 종속변수와 독립변수가 모두 연속변수인 분산 분석(ANOVA,ANCOVA,MANOVA,MANCOVA등) 아우르는 종합적인 버젼 모델을 구하는 수
10.Biostatistics 통계 분석- Propensity Score matching

Propensity score 성향점수 \-연구 대상이 특정 공변량에 의해 대조군이 아니고 실험군에 포함될 확률Propensity Score matching을 적용한 이후에는 bias를 좀 완화할 수 있는 model을 형성할 수 있음 기본 가정1) conditional
11.Biostatistics 통계 분석- 주성분 분석(Principal Component Analysis, PCA)

주성분 분석(Principal Component Analysis): 서로 상관관계를 갖는 많은 변수를 상관관계가 없는 소수의 변수로 변환하는 차원축소 기법변환에 사용하는 소수의 변수를 주성분(Principal component)라고 일컫고 성분이라고도 함주성분은 변수들
12.Biostatistics 통계 분석- ANCOVA (Analysis of Covariance)

ANCOVA의 목적: 실험이 적절하게 통제되서 종속변수의 변동을 설명하는데 문제가 없으면 t-test나 분산분석을 진행하는 경우가 best이나, 여러가지 다른 변인들을 적절하게 통과되어 조사하고자 하는 변수만의 효과를 알아야하는 경우가 있을 수 있다. 통제가 안되는 연
13.Biostatistics 통계 분석- 반복 측정 자료 연구 (1)

같은 개체를 여러 시점에서 반복하여 측정된 자료를 뜻함!장점:)1\. 동일한 개체에 대한 차료의 효과를 비교하는 것이어서 개체 간의 변동이 커도 개체 내의 작은 변동을 분석할 수 있음2\. 각 개체 내의 시간에 따른 변화를 측정할 수 있어서 연구의 정밀도가 높아짐 하나
14.Biostatistics 통계 분석- 반복 측정 자료 연구, Repeated Measures ANOVA 설명 및 개념(2)

정규성 가정과 등분산 가정이라는 분산분석 기본 가정 따름\-정규성: 개체 수가 크다면 무리 없다고 판단\-구형성(Sphericity assumption): 두 시점 사이의 측정치의 차이의 분산이 일정+각 군에 분산 구조가 같다는 동일성 가정 (the assumption
15.Biostatistics 통계 분석- Repeated measures ANOVA 실습

본 데이터의 예저는 UCLA Advanced Research Computing에서 제공하는 tutorial과 데모 데이터를 참고해서 작성하였습니다. 이전 포스트에서 Repeated Measures ANOVA를 간단하게나마 설명했기에 R코드와 결과 값을 기반으로 한 해석
16.Biostatistics 통계 분석- 반복 측정 자료 연구, 선형혼합모형(3)(Linear Mixed effect Model: LMM)

고정 효과(Fixed Effects): 종속/반응 변수에 영향을 미칠 것으로 예상되는 변수 표준 선형 회귀에서 설명 변수무작위 효과(Random Effects, 그룹화 변수로 생각):일반적으로 통제하려는 그룹화 요인 (항상 범주형 요인만 가능) 모든 가능성의 샘플인 경
17.Biostatistics 통계 분석- 임상연구에서 연구 표본 수의 선정 (Calculation of Sample Size in Clinical Trials)

임상 시험 수행 전 표본의 수를 먼저 정하고 임상 연구를 진행하는 게 일반적이므로 필요한 연구 대상자 수의 산출이 중요한 문제! 통계적 가설검정과 오류 먼저 통계적 가설검정과 오류의 개념을 복습해보면... 제 1 종의 오류 (Type I error) 귀무가설이 참인
18.Biostatistics 통계 분석-동등성

임상실험의 목적 -우월성 Treatment A has more therapeutic effect than B coclusion: A>B -동등성 Two treatments A and B have equal therapeutic effect coclusion: A=
19.Biostatistics 통계 분석-연관성의 검정 or 범주형 자료 분석

두 변수의 연관성에 통계적 가설 검정 방법 1. 카이제곱 검정 동질성 검정 (Homogenity Test) EX) 실험 약 집단과 위약 집단에서 심장 병이 발병할 확률이 같은지 검정을 수행할 때 하는 검정:) 귀무가설은 독립성 검정 (Independent Test)
20.Biostatistics 통계 분석-ANOVA (분산분석)

One-way ANOVA 설명변수가 연속형 대신 이산형인 회귀분석이라고 생각하면 되고, two sample t-test의 확장으로 세 그룹 이상의 평균이 모두 같은 지 검정 수행 F-test 그룹 간 변동량과 그룹 내 변동량의 비로, 세 그룹 평균의 차이들의 제곱합인