두 변수의 연관성에 통계적 가설 검정 방법
1. 카이제곱 검정
동질성 검정 (Homogenity Test)
EX) 실험 약 집단과 위약 집단에서 심장 병이 발병할 확률이 같은지 검정을 수행할 때 하는 검정:)
귀무가설은
독립성 검정 (Independent Test)
예를 들어 흡연(X)과 심근경색(Y)의 관계를 연구하는 경우 두 사건이 모두 확률적인 사건이라고 보고 수행하는 가정:)
두 가지 가설을 엄격하게 구별할 이유가 없고
->만약, 귀무가설이 기각되면 두 변수의 연과성은 유의하다고 결론을 내릴 수 있음
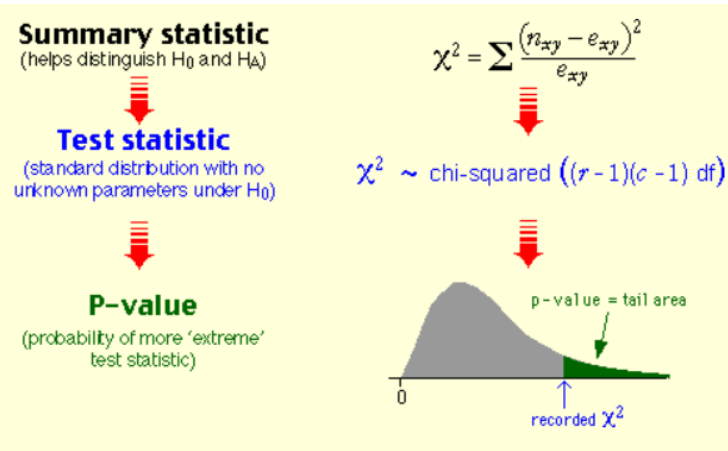

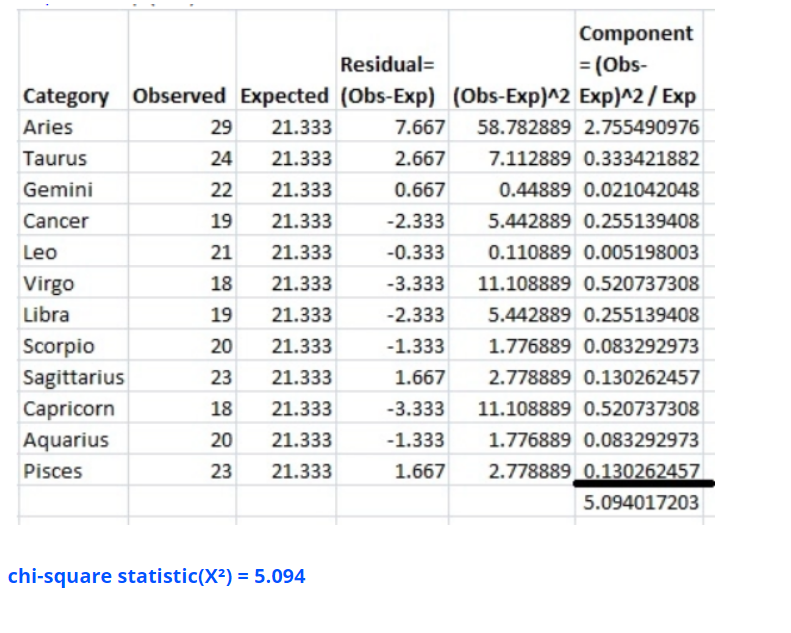
2. 코크란-맨텔-헨젤 검정
범주형 자료에서 RR, OR을 구할 때, 혼란 변수를 보정하는 방법
예를들어, age가 혼란 변수로 의심되어 나이에 따라 Stratification(층화) 진행!
Stratification 후에 각각 계산된 OR 값을 통해 혼란 변수로 인해 OR 값이 과추정 되는 경우가 종종 발생하는데, 이런 두 OR 값을 합쳐서 보정하기 위하여
->코크란-멘텔-헨젤 방법을 통해 공통 OR을 구하는 것!!!
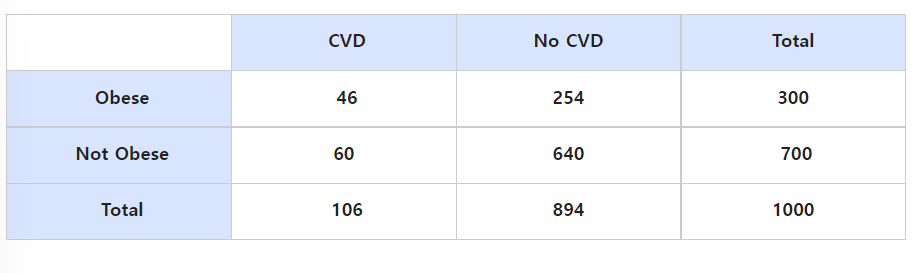
Odds ratio를 구하면 odds(비만)/odds(비만x)
=>46/254 / 60/640 =1.93
나이가 혼란변수로 작용할 수 있어 층화를 진행하고 나이는 50을 기준으로 한다.

동일한 방법으로
Age < 50 : OR = (10/90) / (35/465) = 1.476
Age >= 50 : OR = (36/164) / (25/175) = 1.53
계산됨을 알 수 있고 OR 값이 혼란변수땜에 과추정되었음을 알 수 있다.
그래서 코크란 멘텔 헨젤 방법을 적용하면

이와 같이 보정이 가능하고, 굳이 50이 아닌 다양하게 세분화하여 보정을 적용해 볼수도 있다:)

3. 맥나마 검정
짝 지은 명목형 데이터에서 사용하는 경우
예를 들어, 눈병 치료에 사용되는 A약과 B약의 효과를 비교하기 위하여
각각의 약을 환자의 오른쪽 눈과 왼쪽 눈에 처치를 하고
치료의 여부를 관측하는 case!

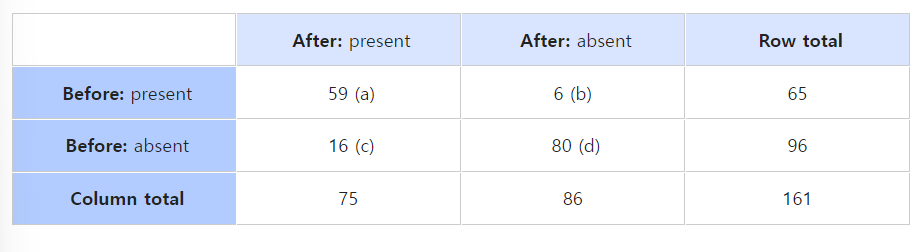
표의 예시를 보면 약물의 처방 전 후의 표:)
검정 통계량을 계산해보면, b=6 c=16 이므로 검정통계량이 100/22=4.55 이고 카이제곱분포에서 p-value계산을 하면 0.33이므로 marginal prob이 같다는 귀무가설 기각 가능!!
출처:
https://3months.tistory.com/230?category=743476
https://3months.tistory.com/229
