자료 출처
오늘은 시계열 데이터를 공부할 예정입니다. 저는 'Forecasting: Principles and Practice'이란 온라인으로 올라온 교재 자료를 보고 오늘 공부를 시작하려고 합니다.

교재는 이렇게 생겼습니다. 줄여서 FPP라고 부르기도 하나 봅니다. 번역판은 나오지 않았지만 이것을 누군가 2017년도에 원서를 한글로 옮기는 작업을 해주셨습니다. 약 2년 동안 번역하셨다고 합니다.
수학 원서는 공부해보신 분은 아시겠지만, 정말 오번역이 많죠! 하지만 이 자료를 읽으며 번역 때문에 이해가 안 가는 일은 없을 것 같습니다. 이해가 안 간다면 내 머리를 탓하리😓 그분이 어디 계신지 모르지만 일단 감사 인사 올리고 공부 시작합니다.
시계열 시리즈
목차
- 예측될 수 있는 것?
- 시계열
- 정상성 시계열
- 차분
- 확률 보행
- 2차 차분
예측될 수 있는 것?
'정상성'과 '차분', 들어본 적 있으신가요? 전 진짜 처음 들어봅니다. 그렇다면 '시계열'은 어떠신가요? 시계열 데이터란 무엇을 의미하나요? 그렇다면 이런 건 도대체 왜 필요한 걸까요? 🤷♀️
일상 생활에서 많은 경우에 예측이 필요합니다. 향후 5년 안에 어떤 발전소를 더 지어야 할지 말지 를 결정하는데도 미래의 수요를 예측해야 합니다.
회사에서도 몇 명의 사원을 더 뽑을 지도 업무량을 파악해서 예측해야 할 것이고(갑자기 떠오른 건데 그러면 Man Month도 시계열 데이터일까요?), 내일 해가 몇 시에 뜰 것인지, 당장 다음 달 생활비를 얼마나 써야 할 지도 예측이 필요합니다!
예측은 쉬운 것도 어려운 것도 있습니다. 오늘 새벽 몇 시 쯤에 환경 미화원이 도착할 지 예측하는 건 쉽겠지만, 로또 번호 예측 같은 건 어럽죠.
어쩄든 예측하는 일은 시간 범위에 따라 실제 결과를 결정하는 요인에 따라 데이터의 패턴 종류에 따라 그리고 그 밖의 많은 양상에 따라 달라집니다.
예측은 어떤 데이터를 사용할 수 있느냐에 따라 예측 기법이 달라집니다. 예측에 상관없는 데이터라면 정성적인 예측 기법을 사용해야겠지만, 정량적인 예측을 사용할 수도 있습니다.
- 과거 수치 정보를 사용할 수 있을 때
- 과거 패턴의 몇 가지 양상이 미래에도 계속될 것이라 가정하는 것이 합리적일 때
대부분의 정량적인 예측 문제는 (시간에 따라 일정한 간격으로) 모든 시계열이나 횡단면(cross-sectional) 데이터를 사용한다고 합니다. 어쨌든 미래 데이터를 예측하는 일이 오늘의 주제이니 시계열 영역에 집중하려고 합니다!
횡단면 데이터란?
동일한 시간, 동일 기간에 여러 변수에 대하여 수집된 데이터를 말합니다.
시계열(Time Series)
시계열(Time-Series)는 시간 순서대로 발생한 데이터의 수열을 뜻합니다. 간단한 수식으로는
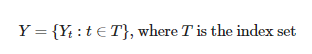
이렇게 표현할 수 있습니다. T는 시간이고 곧 시간이 index가 되는 데이터를 뜻하는 것 같습니다. 꼭 시간일 필요도 없습니다. 날짜도 시계열 데이터가 될 수 있습니다.
시계열 데이터 자료의 예시를 볼까요?
- IBM 일별 주가
- 월별 강우량
- Amazon의 분기별 판매 결과
- Google의 연간 수익
위와 같이 시간에 따라 순차적으로 관측된 것을 시계열로 다룰 수 있습니다. 예를 들면, 시간별, 일별, 주별, 월별, 분기별, 연간 등 일정한 시간 간격이 있는 데이터도 시계열 데이터라 볼 수 있습니다. 시계열 데이터를 예측할 때, 목표는 관측값의 수열이 미래에 계속될 것인지 예측하는 것입니다.
시계열 예측용 모델에는 분해 모델, 지수 평활, ARIMA 모델 등이 있습니다. 제가 오늘 배워야 할 모델은 ARIMA 모델이죠!
시계열 데이터는 이정도 정리하고 넘어가겠습니다.
정상성 시계열(Stationary Time-Series)
노드에서는 Stationary를 이해를 돕기 위해 '안정성'이란 번역을 선택한 것 같습니다. 저는 오늘 개념 이해를 위해 다른 자료를 참고하여 정리할 예정이기 때문에 '정상성'의 번역을 선택하겠습니다.
정상성(Stationary)
정상성(stationarity)을 나타내는 시계열은 시계열의 특징이 해당 시계열이 관측된 시간에 무관합니다.
즉, {Yt}가 정상성을 나타내는 시계열이라면, 모든 s에 대해 (Yt, ..., Yt+s)의 분포에 t가 무관합니다.
이 말은 추세나 계절성이 있는 시계열은 정상성을 나타내는 시계열이 아니라는 점입니다. 그래서 이를 '안정성'이 있다고 설명했던 것 같습니다.
추세와 계절성은 서로 다른 시간에 시계열의 값에 영향을 주기 때문입니다. 그래서 정상성을 나타내는 시계열을 '백색잡음(white noise)'라고 하기도 한답니다. 언제 관찰하든, 시간이 어떻든 똑같이 보이기 때문입니다.
여기서 슬슬 헷갈리기 시작합니다. 앞서는 '일정한 간격'이 있는 데이터라고 시계열 데이터를 설명했는데요. 하지만 주기성 행동을 가지고 있는 시계열은 정상성을 나타내는 시계열입니다.
왜냐하면 주기가 고정된 길이를 갖고 있지 않기 때문에, 시계열을 관측하기 전에 주기의 고점이나 저점이 어디일지 확실하게 알 수 없습니다.
일반적으로 정상성을 나타내는 시계열은 장기적으로 볼 때, 예측할 수 있는 패턴을 나타내지 않을 것입니다. 어떤 주기적인 행동이 있을 지라도요. 시간 그래프는 시계열이 일정한 분산을 갖고 대략적으로 평평하게 될 것을 나타낼 것입니다.
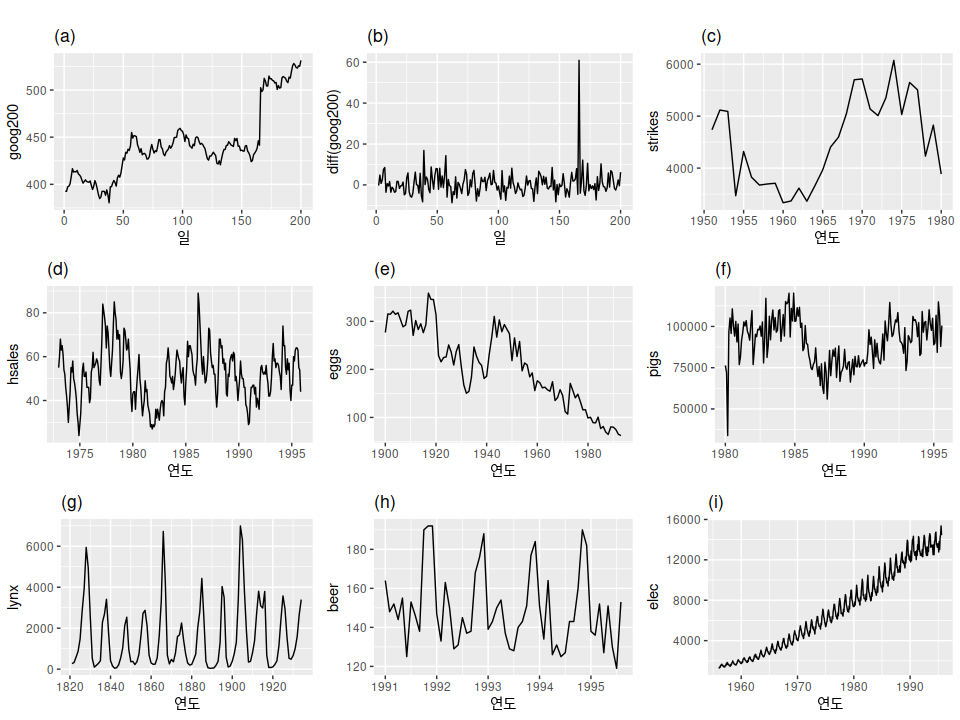
위의 그래프를 통해 어떤 것이 정상성을 나타내는 시계열인지 맞춰봅시다.
(a) 200 거래일 동안의 구글 주식 가격
(b) 200 거래일 동안의 구글 주식 가격의 일일 변동
(c) 미국의 연간 파업 수
(d) 미국에서 판매되는 새로운 단독 주택의 월별 판매액
(e) 미국에서 계란 12개의 연간 가격(고정 달러)
(f) 호주 빅토리아 주에서 매월 도살한 돼지의 전체 수
(g) 캐나다 북서부의 맥킨지 강 지역에서 연간 포획된 스라소니의 전체 수
(h) 호주 월별 맥주 생산량
(i) 호주 월별 전기 생산량
어떤 것이 계절성이 보이나요? 제 눈에는 (d), (h), (i)가 보입니다. 또한, 추세가 있고 꾸준히 변화하는 (a), (c), (e), (f)도 후보가 되지 못합니다. 그렇다면 남는 모델이 (b)와 (g)만 정상성을 나타내는 시계열 후보가 되겠습니다.
그런데 솔직히 (g)는 뭔가 주기성이 있어보이지 않나요? 여기도 주기(cycle)이 있긴 하지만 이 주기가 불규칙적이기 때문에 정상성이 있다고 본다고 합니다.
저는 주식 가격의 변동은 예측할 수 없기 때문에 정상성 시계열이라 생각했는데, 추세가 있기 때문에 시계열에서 제외된다고 하니 좀 놀랐습니다!
차분(differencing)
아까 위의 그림에서 '(a) 200 거래일 동안의 구글 주식 가격'이 정상성을 나타내는 시계열이 아니었습니다. 하지만 '(b) 200 거래일 동안의 구글 주식 가격의 일일 변동'은 정상성 시계열 데이터였습니다!
교재에서는 이 사실에 주목❗ 해달라고 하네요.
아래의 이미지는 정상성을 나타내지 않은 시계열을 정상성을 나타내도록 하는 한 가지 방법을 보여주고 있습니다.
그 방법은 연이은 관측값들의 차이를 계산하는 것입니다. 이것을 '차분(differencing)'이라합니다. 수열에서 연속하는 두 항의 차라고 이해하면 되겠습니다.
로그 변환은 시계열의 분산 변화를 일정하게 만드는데 도움이 될 수 있습니다.
차분(differencing)은 시계열의 수준에서 나타내는 변화를 제거하여 시계열의 평균 변화를 일정하게 만드는 것을 돕는다고 합니다!
결과적으로 추세나 계절성이 제거(또는 감소)되는 것입니다.
정상성을 나타내지 않는 시계열을 찾아낼 때, 데이터의 시간 그래프를 살펴보는 것만큼 ACF 그래프도 유용하다고 합니다. ACF는 자기 상관 함수를 뜻합니다!
ACF는 어떤 무작위의 신호가 두 시각에 취하는 값의 상관계수를 나타내는 함수입니다.
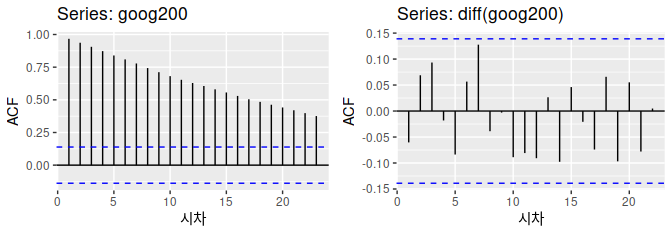
[Figure: 구글 주식 가격의 ACF (왼쪽) 그리고 일별 변동 (오른쪽).]
정상성을 나타내지 않는 데이터에서는 ACF가 느리게 감소하지만, 정상성을 나타내는 ACF가 비교적 빠르게 0으로 떨어질 것입니다. 그리고 정상성을 나타내지 않는 데이터에서는 종종 큰 양수 값을 갖기도 합니다.
참조
Box.test(diff(goog200), lag=10, type="Ljung-Box")
#>
#> Box-Ljung test
#>
#> data: diff(goog200)
#> X-squared = 11, df = 10, p-value = 0.4차분을 구한 구글 주식 가격의 ACF는 단순히 백색잡음(white noise) 시계열처럼 생겼습니다. 95한계 바깥에 자기상관 값이 없고, 0.355라는 p- 값을 같습니다. 이 결과는 구글 주식 가격의 일일 변동이 기본적으로 이전 거래일의 데이터와 상관이 없는 무작위적인 양이라는 것을 뜻합니다.
확률보행
차분(difference)를 구한 시계열은 원래의 시계열에서 연이은 관측값의 차이이고,
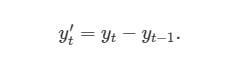
이렇게 씁니다. 첫 번째 관측값에 대한 차분 y1'을 계산할 수 없기 때문에 차분을 구한 시계열은 T-1개의 값만을 가집니다.
차분을 구한 시계열이 정상성이면 원래 시계열에 대한 모델은 아래와 같이 씁니다.
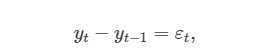
여기서 εt은 백색잡음(white noise)을 의미합니다. 이것을 정리하면 '확률보행(random walk)' 모델을 얻습니다.
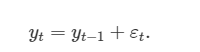
확률보행(random walk) 모델은 정상성을 나타내지 않는 데이터, 특별히 금융이나 경제 데이터를 다룰 때 널리 사용됩니다. 확률보행에는 아래와 같은 두 가지 특징이 있습니다.
- 누가 봐도 알 수 있는 긴 주기를 갖는 상향 또는 하향 추세가 있습니다.
- 갑작스럽고 예측할 수 없는 방향 변화가 있습니다.
미래 이동을 예측할 수 없거나 위나 아래로 갈 확률이 정확하게 같아서 확률보행 모델에서 낸 예측값은 마지막 관측값과 같다고 볼 수 있습니다. 이 모델은 단순(naive) 예측값을 뒷받침합니다.
밀접하게 연관된 모델은 차분값이 0이 아닌 평균값을 갖게 합니다.
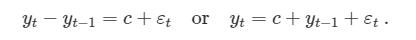
c값은 연이은 관측값의 차이의 평균입니다. c가 양수이면, 평균 변화는 yt 값에 따라 증가합니다.
그래서 yt는 위쪽 방향으로 이동하는 경향을 나타냅니다. 하지만 c가 음수이면, yt는 아래쪽 방향으로 이동하는 경향을 나타내겠죠.
2차 차분
가끔 차분(difference)을 구한 데이터가 정상성이 없다고 보일 수 있습니다. 정상성을 나타내는 시계열을 얻기 위해서 어떻게 해야할까요?
데이터에서 한 번 더 차분을 구하는 작업이 필요할 수 있습니다.
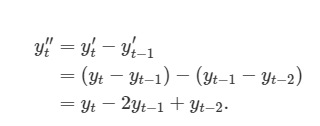
이 식을 보니까 2차 차분이 어떤 것인지 이해가 되시나요? 원래의 차분은
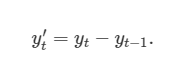
아래와 같았죠.
이 경우에는 yt''는 T-2개의 값을 가지게 될 것입니다. 그러면, 원본 데이터에서 '변화에서 나타나는 변화'를 모델링하게 됩니다. 실제로는 2차 차분 이상으로 구해야하는 경우가 많지 않다고 합니다.
E14를 공부하면서 어떤 것부터 공부를 해야 할 지 감이 안 왔습니다. 일단 진도를 크게 한 번 훑은 다음에 시계열 데이터, 정상성, 차분에 대해 먼저 정리를 해야겠다 싶어서 포스팅을 하게 되었습니다. 다른 분들께도 도움이 되면 좋겠습니다!
