0. reference

• https://preventionyun.tistory.com/31

• 
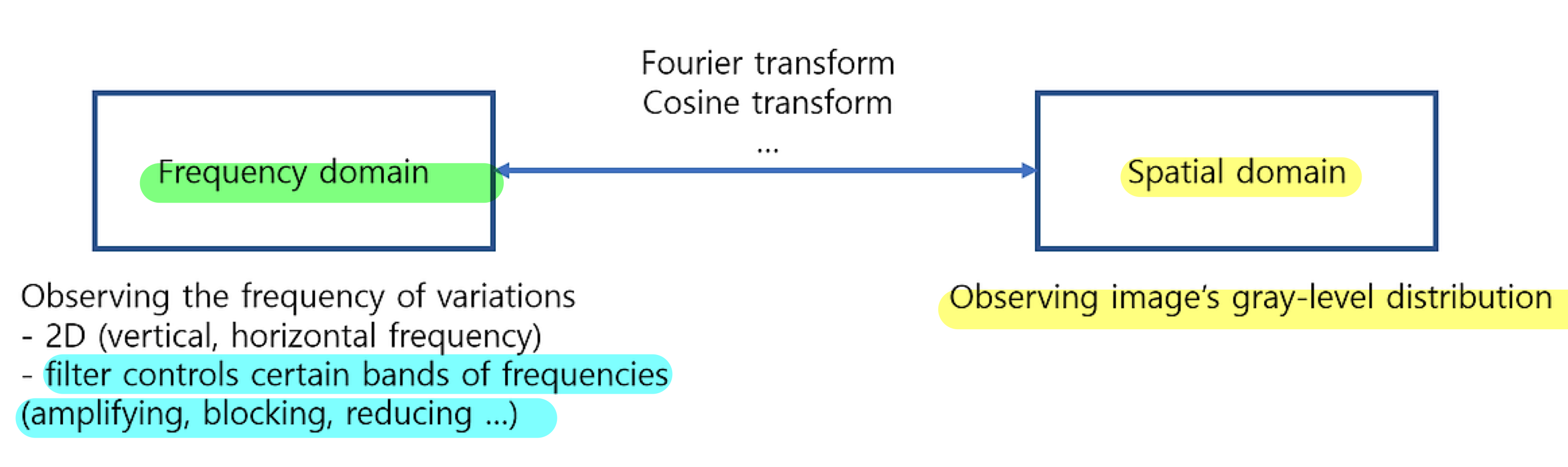
• 우선 filtering에 앞서 신호 및 시스템의 관점에서 frequency와 spatial domain이 무엇인지 살펴보자.
• 영상의 픽셀은 0 ~ 255(8bit, gray scale 기준)의 밝기로 이루어져 있다.
• 이것의 모임이 우리가 보는 영상이 되는 것인데, 신호 관점에서 바라볼 수도 있다.
  • 하늘과 같은 영역은 신호가 대부분 변하지 않는 영역이며,
  • 작은 물체들이 있는 scene의 경우는 신호가 급격하게 변하는 구간이다.
• Frequency domain과 spatial domain의 전환은 Fourier transform과 같은 방식을 통해 전환할 수 있으며,
  • spatial domain에서는 gray-level의 분포를 관찰하는 것이며,
  • frequency domain에서는 variation(변화)의 frequency(빈도)를 관찰하는 것
• 영상의 경우 2차원이기 때문에 frequency 또한 2차원으로 생각하며,
• filter를 사용하여 특정 주파수 대역의 증폭, blocking, 감소를 할 수 있다.

1. low pass filter

• 신호 변화(gradient)의 진폭을 줄이기 위해서 사용
• 즉, 큰 graident를 작게 만든다!

1.1. Mean filter

• 신호 변화의 진폭을 줄이기 위해서 간단한 방법으로는,
  • 큰 graident에 해당하는 픽셀의 값을 주위 픽셀의 평균 값으로 대체하는 방식
• 
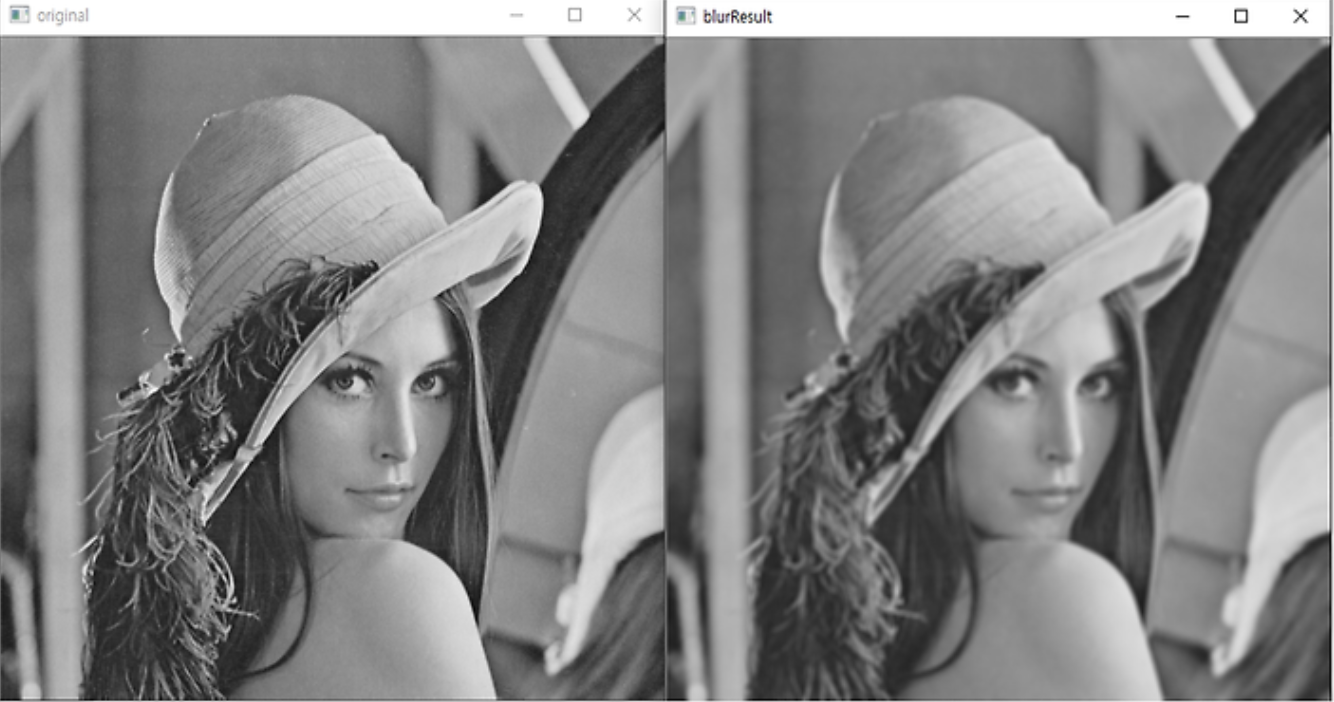
• openCV에서는 blur라는 함수를 제공
• 
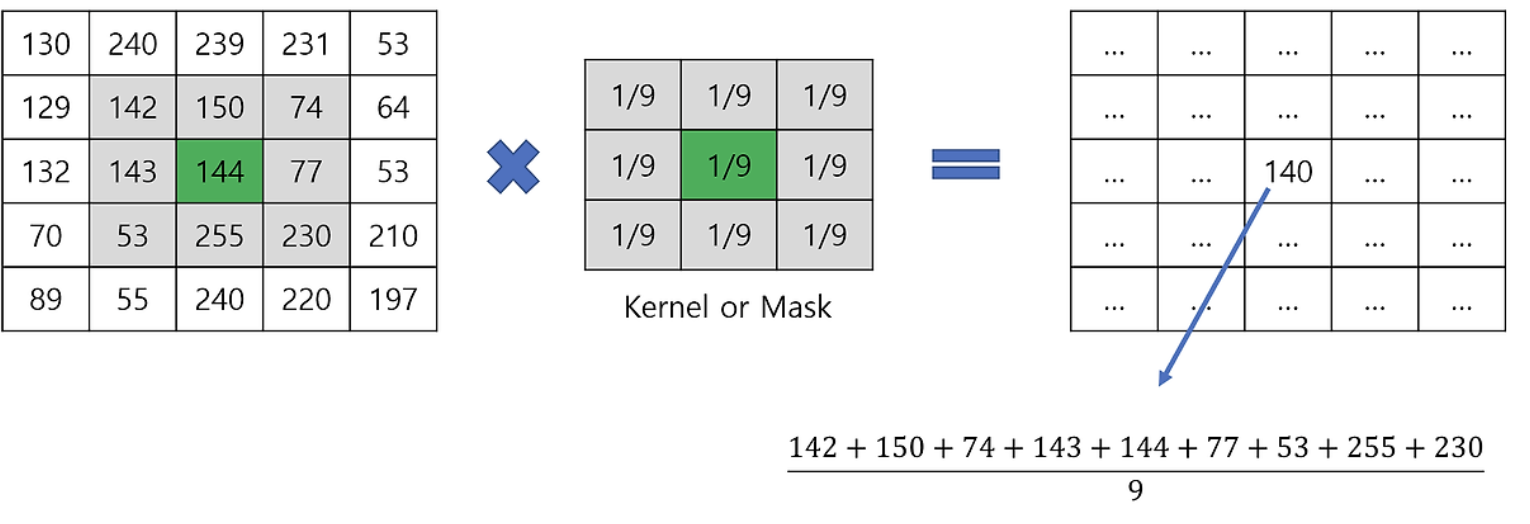
• Mean filter의 경우 weight가 모두 동일하며, 위 그림과 같이 계산이 된다.

1.2. Gaussian filter

• 
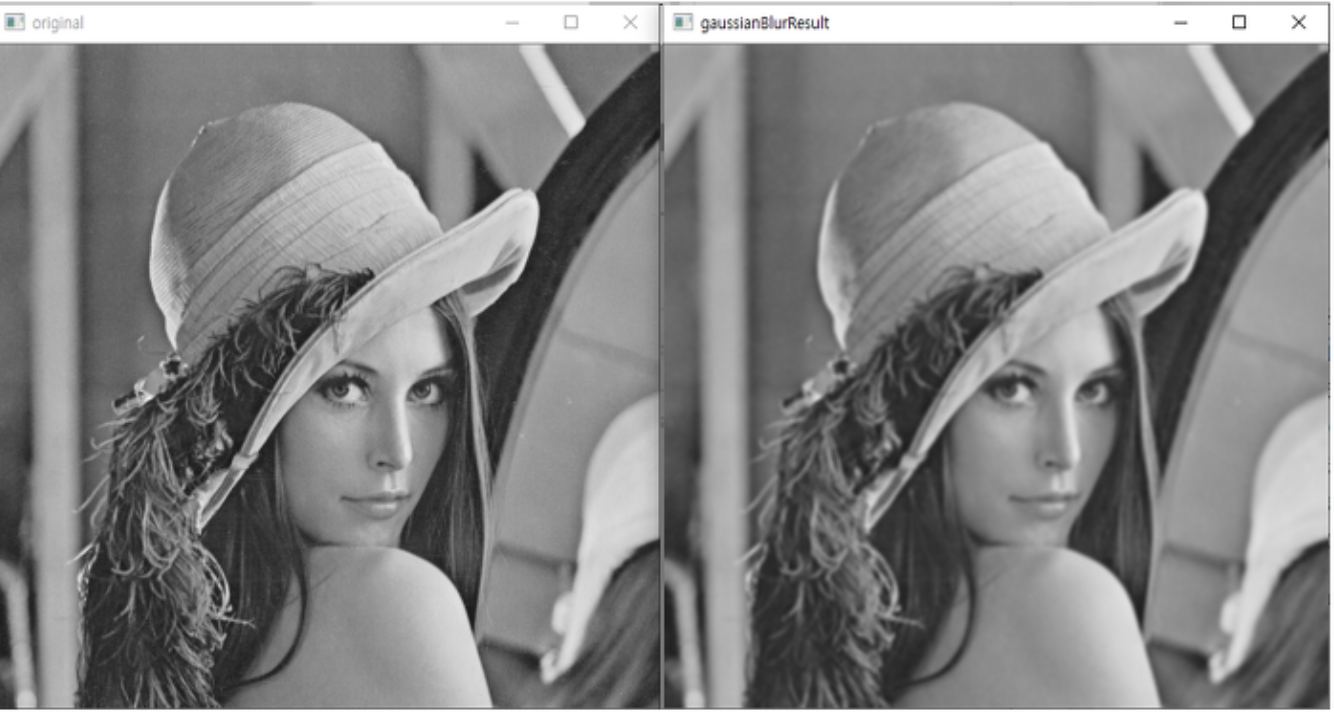
• Gaussian filter의 경우 Gaussianblur 함수를 통해 사용할 수 있다. 사용법 또한 비슷하며, sigma value가 추가된다.
• 
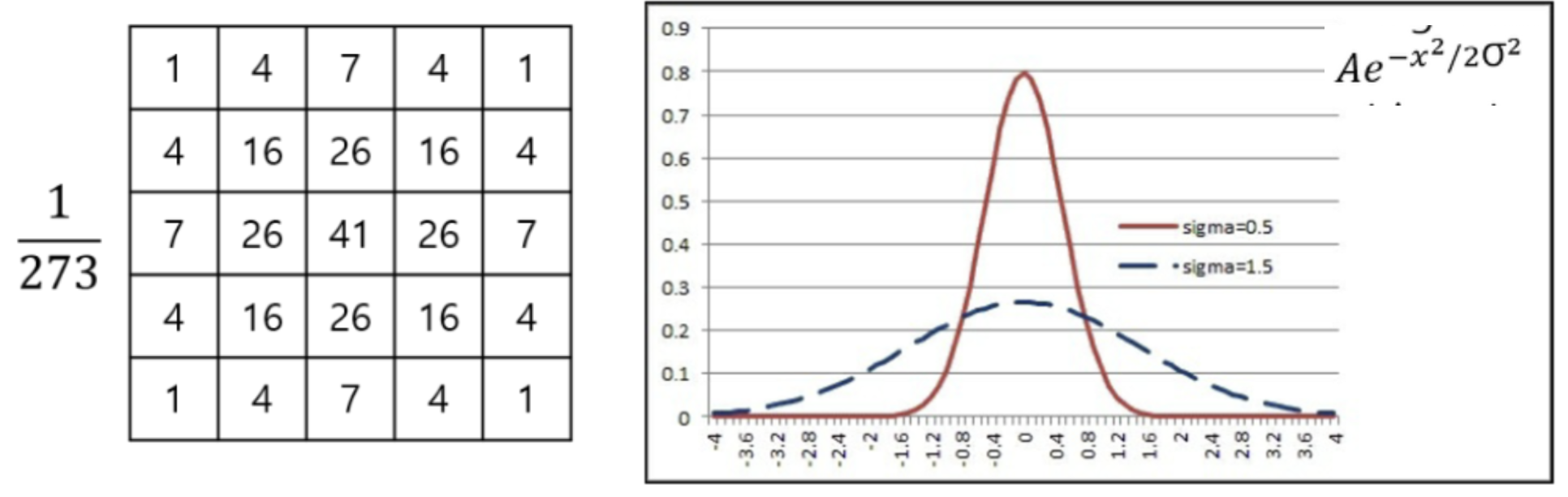
• gaussian distribution은 중심을 기준으로 대칭을 이루며, 면적은 1(확률 및 통계)이 된다.
• 여기서 그래프는 중심에 더 집중된 것(빨강)과 더 넓게 분포된 것(파랑) 모양이 존재할 수도 있는데, 이것을 sigma value를 통해 조절하는 것
  • sigma가 클수록, 더 평평하게 분포한다.
• getGaussianKernel 함수를 통해 size와 data type, sigma를 지정하여 kernel을 생성할 수 있다.
• mean filter와 다르게, gaussian의 경우 중심에 더 많은 weight를 주고 거리가 멀어질 수록 weight가 감소하는 kernel임을 확인할 수 있다.

1.3. Mean VS Gaussian

• Mean filter의 경우 detail이 조금 더 떨어지는 것을 볼 수 있다.
• Gaussian filter
  • center에서 멀어질 수록 weight를 감소시켜
    • pixel간 transition이 조금 더 smooth
• Mean filter
  • 같은 weight로 해당 신호를 주위 신호의 평균으로 대체해버리기 때문에 급격한 변화가 발생
  • frequency 관점에서 mean filter는 모든 high frequency components를 제거하지 못했다고 볼 수 있다.
• 이해가 잘 안된다면 흑과 백이 양쪽으로 존재하는 영역에서 filter를 적용한다고 생각해보자.
  • Mean filter의 경우 경계선에서 흑과 백의 평균인 회색으로 나타날 것이며,
  • Gaussian filter의 경우 좀 더 smooth하게 변하는 결과가 보여질 것이다.