[2025 ICCV] Scheduling Weight Transitions for Quantization-Aware Training

Hyungseop Lee·2025년 12월 30일

[Paper Review] Model Compression - Quantization, etc

목록 보기
6/6
post-thumbnail

Paper Info.

https://openaccess.thecvf.com/content/ICCV2025/papers/Lee_Scheduling_Weight_Transitions_for_Quantization-Aware_Training_ICCV_2025_paper.pdf

Abstract

(background: QAT 학습 과정?)

  • QAT는 학습 과정 중에 quantization process를 simulate하여 weights/activations의 bit-precision을 낮추는 방법이다.
    QAT는 latent weights를 updating 함으로써 간접적으로 quantized weights를 학습한다.
    즉, full-precision inputs을 quantizer에 입력하여, gradient-based optimizers를 통해 학습한다.

(문제 제기: QAT에서 LR scheduling 방식이 적합하지 않다.)

  • "We claim that coupling a user-defined learning rate (LR) with these optimizers is sub-optimal for QAT."
    Quantized weights는 대응되는 latent weights가 transition point를 통과할 때에만 quantizer의 discrete levels로 transit한다.
    이 transition point는 quantizer가 discrete states를 변경하는 위치이다.
    이는 quantized weights의 변화가 latent weights에 적용되는 LR 뿐만 아니라, latent weights의 distributions에도 영향을 받는다는 것을 의미한다.
    따라서 learning rate를 manually scheduling하는 것만으로는 quantized weights의 변화 정도를 제어하기 어렵다.

(가설 및 제안: weight transition 횟수를 scheduling하자.)

  • 우리는 QAT에서의 parameter 변화의 정도가 discrete levels 간 transiting을 발생시키는 quantized weights의 개수와 밀접하게 관련되어 있다고 가정한다.
    이를 바탕으로, quantized weights의 transition 횟수를 명시적으로 제어하는 Transition Rate (TR) scheduling 기법을 제안한다.
    latent weights에 대한 LR을 scheduling하는 대신, quantized weights의 target TR을 scheduling하고,
    이에 맞추어 Transition-Adaptive Learning Rate, TALR을 사용해 latent weights를 update한다.
    이를 통해 QAT 과정에서 quantized weights의 변화 정도를 직접 considering할 수 있다.

motivation이 뭔데?

1. Introduction

(B.G.: QAT 과정)

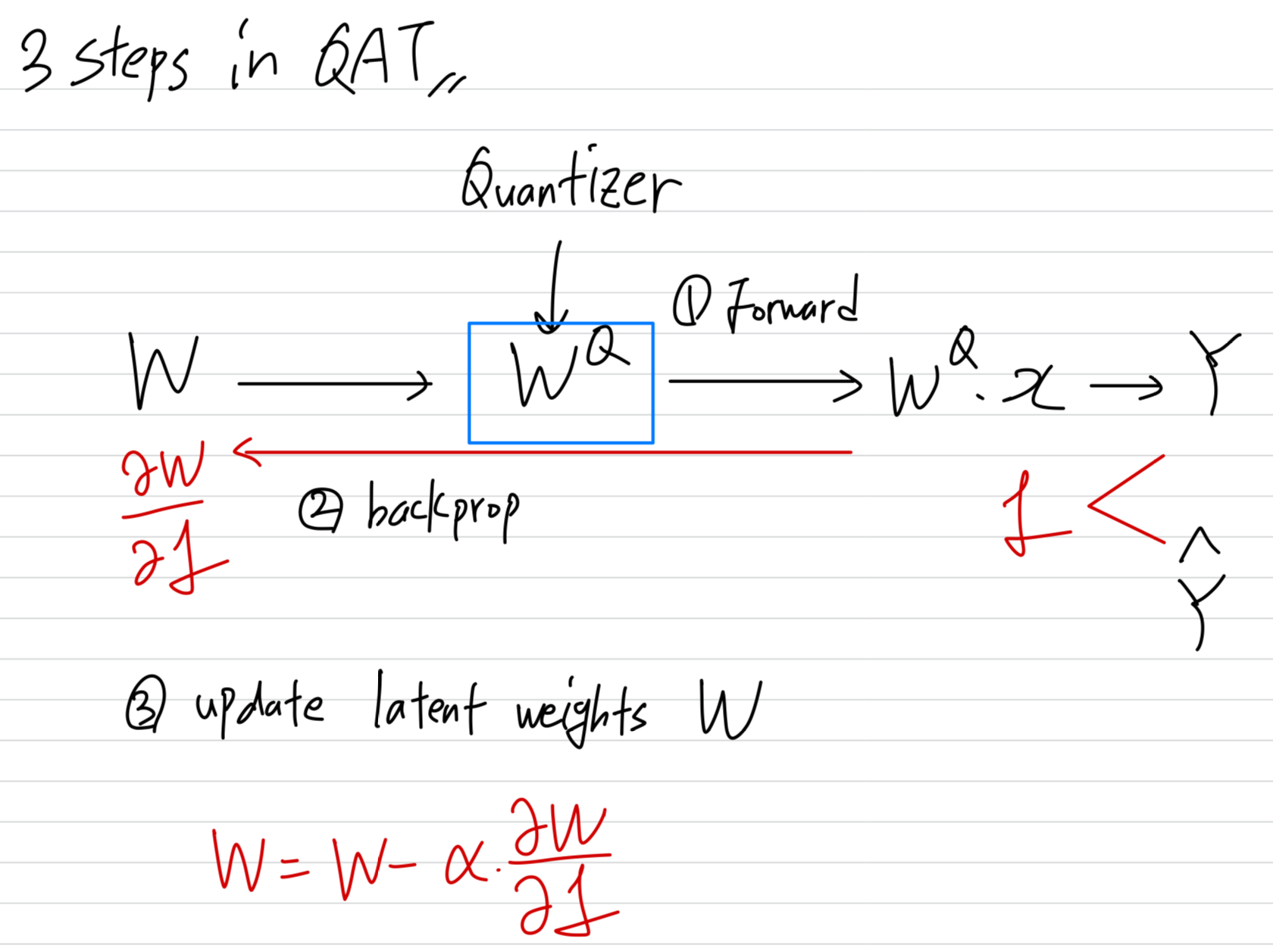
  • QAT mainly consists of three steps:
    1. In a forward propagation step,
      full-precision latent weights are converted to quantized weights using a quantizer,
      and the quantized weights are used to compute an output
      (quantizer로 full-precision latent weights를 quantization함.
      quantized weights로 prediction)
    2. In a backward propagation step:
      Gradients w.r.t an objective function are then back-propagated to the latent weights.
      (full-precision latent weights에 대한 gradient를 back-propagation함)
    3. In an optimization step:
      the latent weights are updated with the gradients.
      (back-prop으로 구한 gradients로 full-precision latent weights를 update)

(이전 연구의 한계점)

  • 이전 연구들은 quantizers를 designing함으로써 forward and backward propagation steps에 집중했고
    quantizer에서 deiscretization function으로 인해 발생하는 a vanishing gradient problem을 해결하려 했다.
    이들은 optimization step에 대해서 pay attention하지 않았고,
    단순히 latent weights를 update하기 위해,
    SGD or Adam과 같은 gradient-based optimizers with a user-defined learning rate(LR)을 사용    했다.

  • 하지만 이러한 optimization strategy는 full-precision models을 training하기 위해 designed되었고,
    quantized weights가 얼만큼 변하는지는 고려하지 않았다.
    이는 QAT에서 sub-optimal을 초래한다.
    (질문: 결국 우리가 optimize해야 할 것은 quantized weights인데,
    이전 연구들은 full-precision model을 training하기 위해 design했으니 suboptimal하다고 주장하는 것인가? 내가 제대로 이해한건가..?)
    (질문: 왜 quantized weights의 변화 횟수를 고려해야 되는데?)

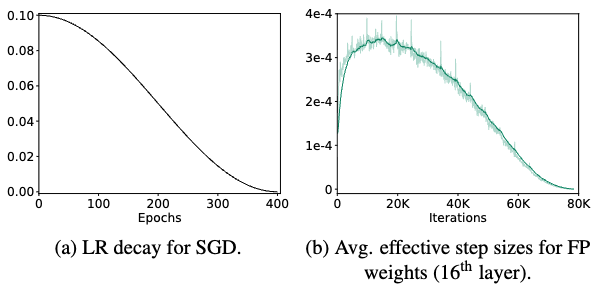
(FP model에서 LR과 effective step size의 높은 correlation)

  • gradient-based optimizer로 full-precision model을 training시킬 때,
    우리는 일반적으로 LR을 progressively decay시켜 weight를 coarse-to-fine으로 update하며,
    이를 통해 model의 convergence를 보장한다.
    즉, a single parameter change(변화)의 magnitude(크기)인 이른바 effective step size가
    LR과 높은 correlation을 가지므로, LR scheduling을 통해 weights의 변화 정도를 수동으로 제어할 수 있다.
    예를 들어, weight 변화의 정도를 정량화한 average effective step size는 small LR에서가 large LR에서보다 작다.
    (내가 이해한 내용: full-precision model에서는 effective step size(=weight update 크기=ΔW\Delta W)가 당연히 LR과 매우 높은 correlation을 가짐.
    W=W−α×ΔWW=W-\alpha\times \Delta W 이니까.)

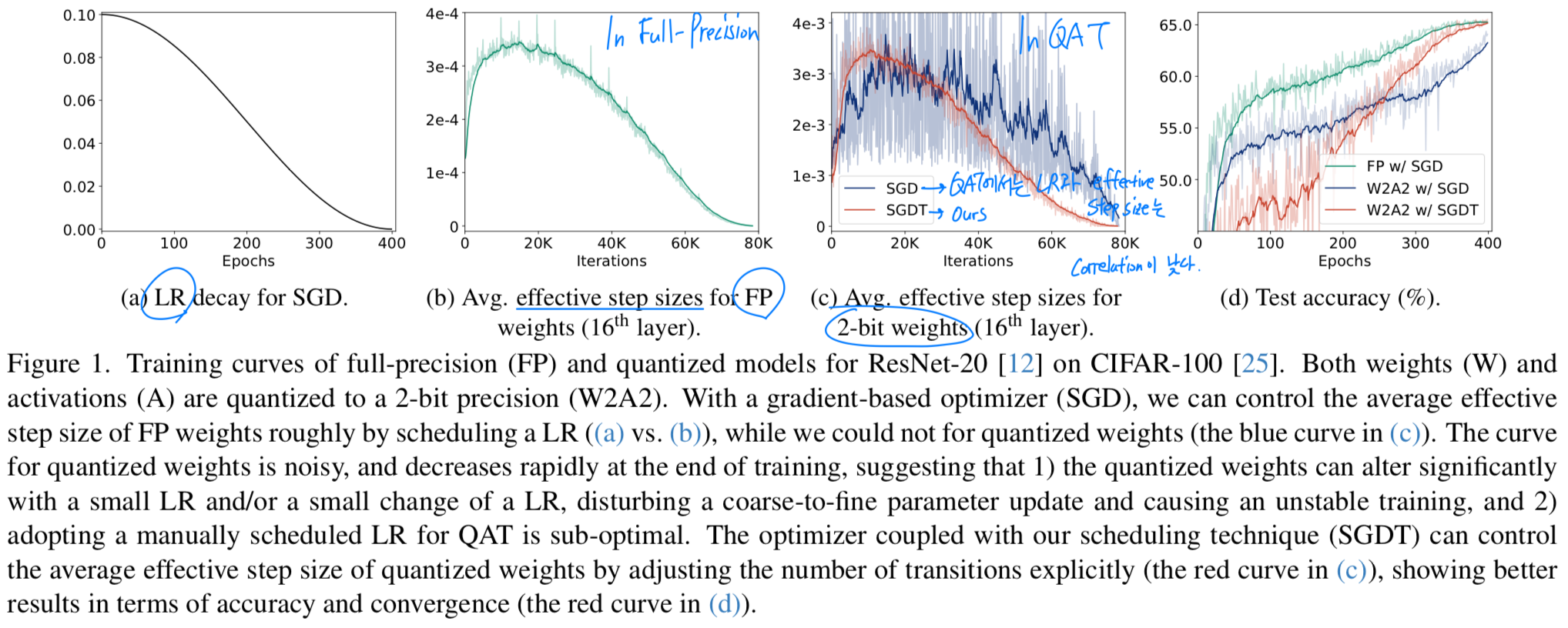
(QAT에서 LR과 effective step size의 낮을 수 밖에 없는 correlation)

  • 그러나 이러한 특성은 QAT(Quantization-Aware Training)에서 LR과 결합된 optimizers를 적용할 경우에는 성립하지 않는다는 점을 발견했다.
    QAT는 latent weights와 quantizer를 통해 quantized weights가 indirectly update되기 때문에,
    quantized weights의 average effective step size는 latent weights보다 LR과 less correlated    된다.
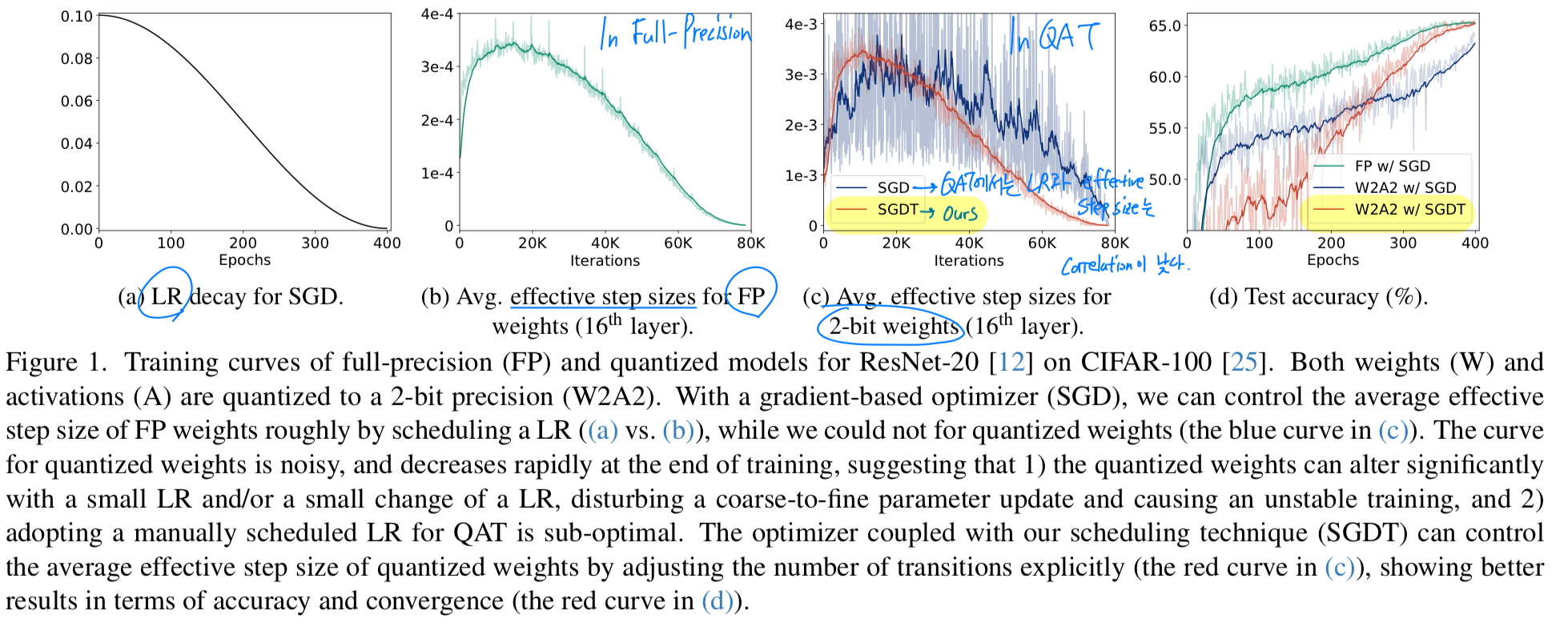
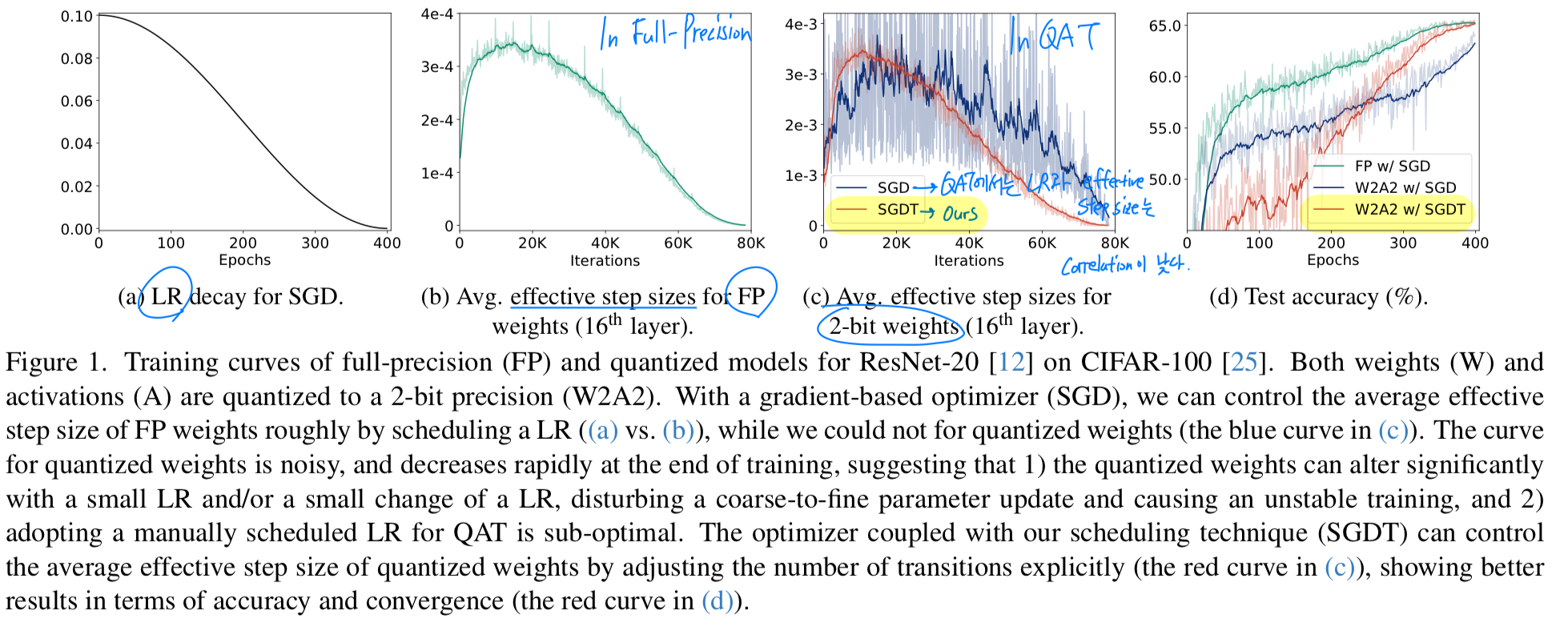
    (Fig. 1a와 Fig. 1c의 blue curve 비교)

  • 보다 구체적으로 말하면,
    full precision weights와 달리,
    quantized weights는 해당 latent weights가 discrete states를 변경하는 지점, 즉 transition point을 pass할 때에만 discrete levels이 바뀐다.
    이를 transitions이라 부른다.
    이로 인해 LR을 조정하는 것만으로 average effective step size of quantized weights를 조절하는 것은 어려워지며,
    이는 training 전반에 걸쳐 거친 단계에서 coarse-to-fine parameter updates를 방해하고,
    training의 후반에도 model의 convergence를 방해할 수 있다. (Fig. 1d의 blue curve)
    예를 들어, latent weights가 transition point에 집중되어 있는 경우, 매우 작은 LR에서도 해당 transition point를 쉽게 통과하게 되어,
    quantized weights에 significant changes가 생길 수 있다.
    (→\to 이게 QAT에서 oscillation 문제를 말하는 듯)

(제안: transition rate=TR scheduling)

  • 이 연구에서, 우리는 QAT를 위한 a transition rate (TR) scheduling technique을 제안한다.
    TR scheduling은 quantized weights의 transitions을 명시적으로 고려하면서 latent weights를 update할 수 있도록 한다.
    우리는 quantized weights의 TR을 각 interation마다 discrete levels이 변경된 quantized weights의 개수를 전체 weights 개수로 나눈 값으로 정의한다.
    quantized weight의 effective step size는 0이거나 a discrete value (two quantization levels 간의 거리) 중 하나이므로,
    quantized weight의 average effective step size는 #(transitions)에 의해 주로 결정    된다.
    이에 따라 우리는 #(transitions)이 quantized weights에서 parameter changes의 정도를 제어하는 key라고 가정한다.

(제안: transition-adaptive learning rate = TALR)

  • 이러한 관찰에 기반하여,
    우리는 latent weights에 대한 LR을 scheduling하는 대신, quantized weights의 target TR을 scheduling하고,
    이에 맞춰 quantized weights의 TR을 adjust할 수 있도록
    a novel transition-adaptive learning rate (TALR)을 사용하여 latent weights를 update한다.
    TALR 현재 quantized weights의 TR이 target TR과 일치하도록 adaptively 변화한다.
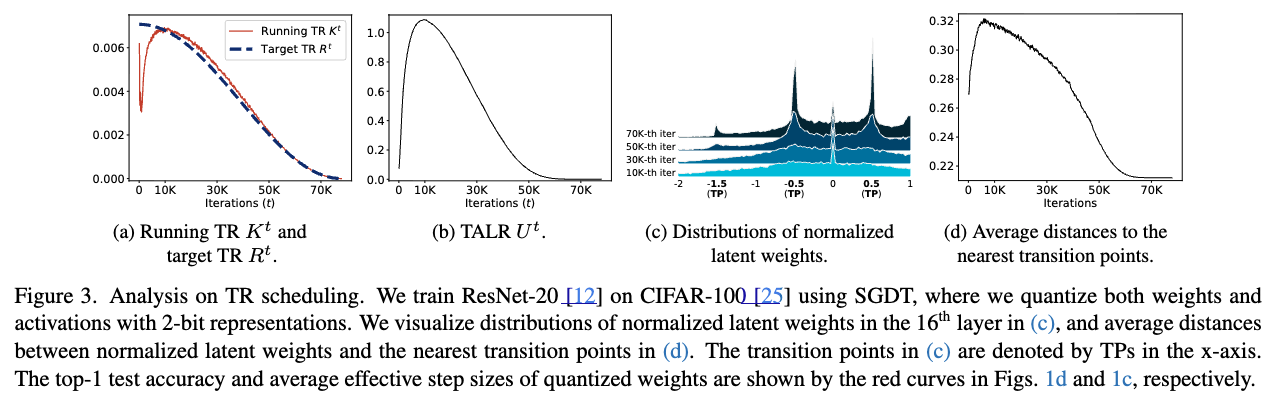
    target TR을 scheduling함으로써, 우리는 quantized weights의 average effective step size를 직접적으로 조절할 수 있으며 (Fig. 1c의 red curve),
    이를 통해 quantized weights를 coarse-to-fine manner로 optimize할 수 있고, stable training process를 달성할 수 있다 (Fig. 1d의 red curve)

  • 우리가 아는 한, a full-precision training에서와 같이 LR을 scheduling하는 대신 QAT에서 TR을 scheduling하는 접근은 기존 연구에서 시도된 바 없다.
    우리는 다양한 network architectures에서 여러 optimizers (SGD, Adam, and AdamW)을 사용하여,
    제안한 TR scheduling 기법이 plain LR scheduling보다 우수함을 실험적으로 입증한다.

2. Related Work

QAT

  • QAT의 연구 흐름 (fixed quantizer, learnable quantizer...)과 한계점

  • QAT의 oscillation 문제와 관련 연구, 한계점

  • osciilation 문제와 관련 연구 PQT와 한계점

...

Optimization Methods

skip

3. Preliminary

Quantizer


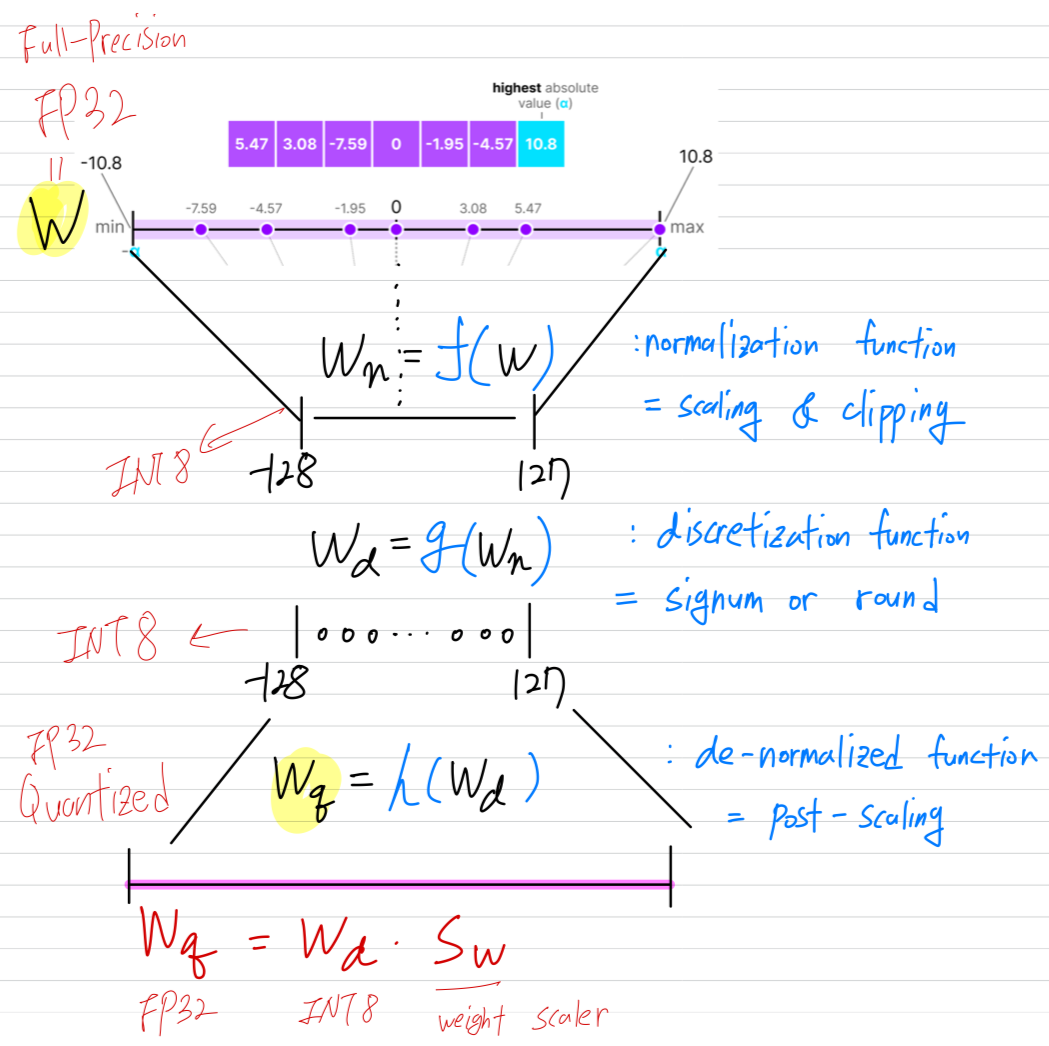
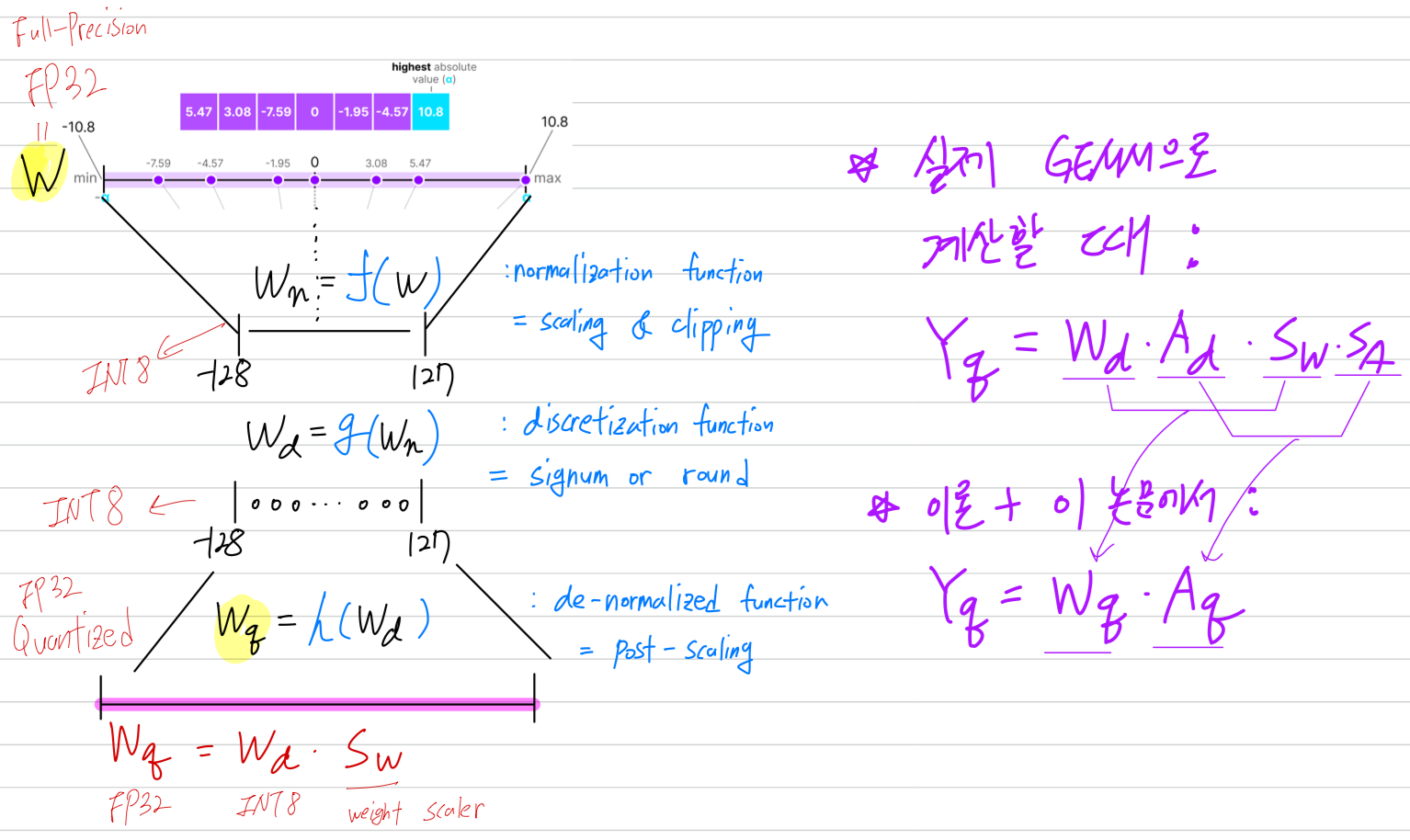
GEMM vs. 이론

  • GEMM (GEneral Matrix Multiplication)으로, GPU 또는 TPU 같은 AI accelerator의 tensor core는
    한 CLK에 GEMM 연산을 한 번에 수행하도록 설계 됨.
    DL model이 inference할 때, 내부적으로 GEMM 연산을 수십억 번 반복하는 것임...
  • 아래는 실제 GEMM 구현과 이론(paper)에서 나타내는 수식의 순서가 다르다는 것을 보여줌.
    왜 이렇게 다르게 쓰지? quantization 연구하는 연구실 동기의 답변: "논문에서 설명하기 편하니까"

Optimizer

4. Method

4.1. Empirical analysis

  • full-precision model에서는 weights가 continuous values이기 때문에,
    LR은 weights를 update하는 데에 즉각적으로 영향을 준다.
    반면, 심지어 small LR이더라도 quantized weights는 급격하게 변한다.
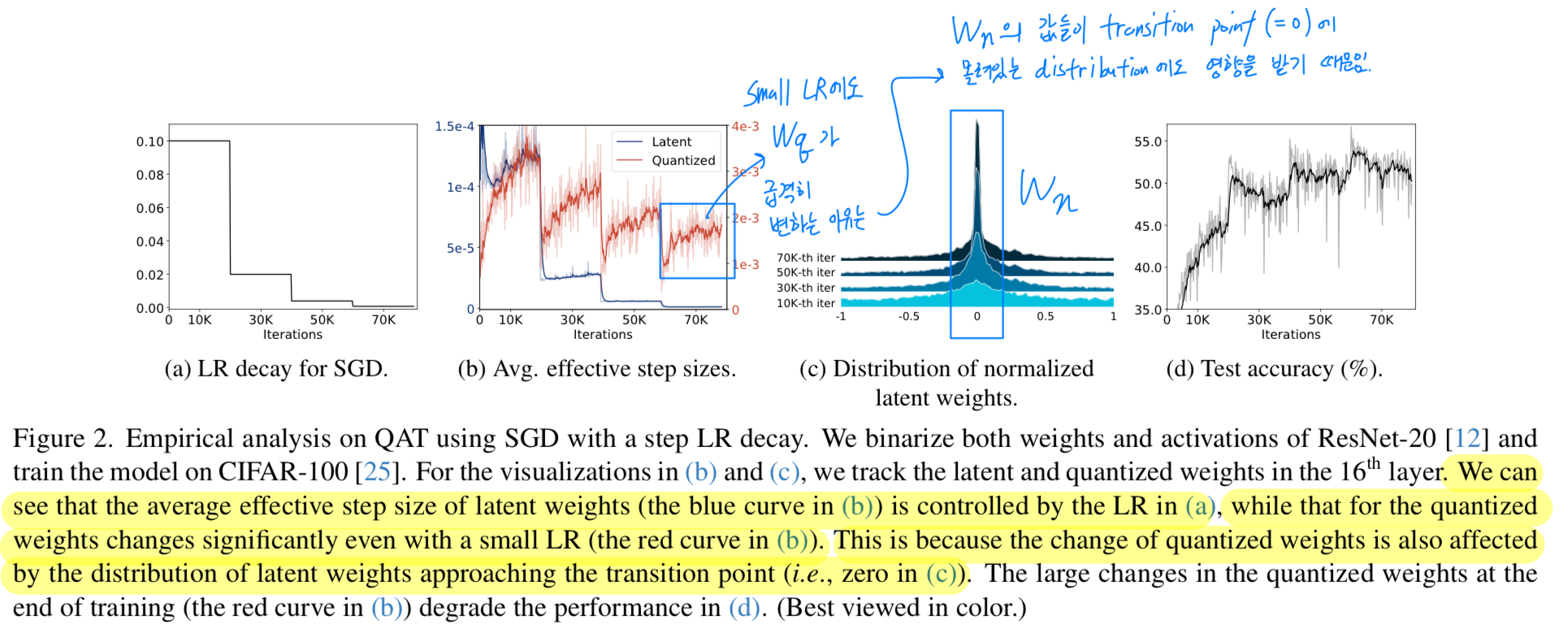
    "the large changes of quantized weights at the end of training make a training process unstable (Fig.2d)"

  • 이 문제를 깊게 파보기 위해, training loss를 최소화하기 위해
    quantized weights가 discrete level을 변경해야 하는 상황을 가정해보자 (from a negative value to a positive one in the binary quantization).
    이때 대응되는 latent weight는 transition point를 향해 이동하기 위해 gradient를 계속 accumulating하게 되며,
    일단 transition이 발생한 이후에는 latent weight가 그 transition point 근처에 머무를 수 있다.
    Fig. 2에서 확인할 수 있듯이, the normalized latent weights (wnw_n)는 iterations 횟수가 증가함에 따라 점진적으로 transition point (zero in this case)를 향해 가까워진다.
    그 결과, 학습 후반부에서는 small LR을 사용하더라도 quantized weights가 adjacent discrete levels 사이에서 oscillate할 가능성    이 커진다
    (Fig. 2c의 70K-th iteration에서 나타나는 high peak)

  • This analysis indicates that
    1) the average effective step size of quantized weights is largely affected by the distribution of latent weights, and
    2) the reason why the LR is not a major factor for controlling the average effective step size in QAT

4.2. TR scheduler

  • 우리는 effecitve step size와 quantized weights의 transitions 간의 relationship을 나타낸다.

TR of quantized weights

  • 우리는 update 이후에 discrete weights (wdw_d in Eq. (2))가 changed했는지? not changed했는지?를 관찰함으로써
    the number of transitinos을 count    할 수 있다.

  • 우리는 TR = #(transitions) / #(total quantized weights)을
    다음과 같이 정의    할 수 있다:

Relation between an effective step size and a transition

  • transition 횟수를 조절하는 것은 effective step size를 조절하는 것에 중요함.

TR scheduler

  • 우리는 latent weights를 update하기 위해 a transition-adaptive learning rate (TALR)을 도입함으로써
    optimization process에 TR scheduling techinque을 적용했다.
    TALR은 target TR에 대해서 TR of quantized weights를 수동적으로 조절할 수 있다.

  • 이를 위해 매 iteration 마다 세 가지 주요 연산을 수행한다:

    1. momentum estimator
    • 구체적으로, 우리는 먼저 iteration tt에서의 quantized weights의 running TR을
      momentum mm을 갖는 exponential moving average로 계산한다.
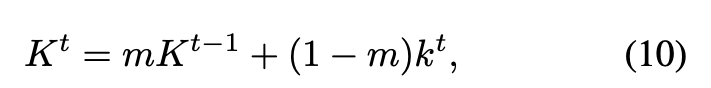      여기서 KtK_t는 running TR (즉, 현재의 TR)을 의미한다.
    1. adjusting a TALR w.r.t a target value
      그리고나서, 우리는 running TR KtK^t와 target TR에 기반한 TALR을 조절한다:
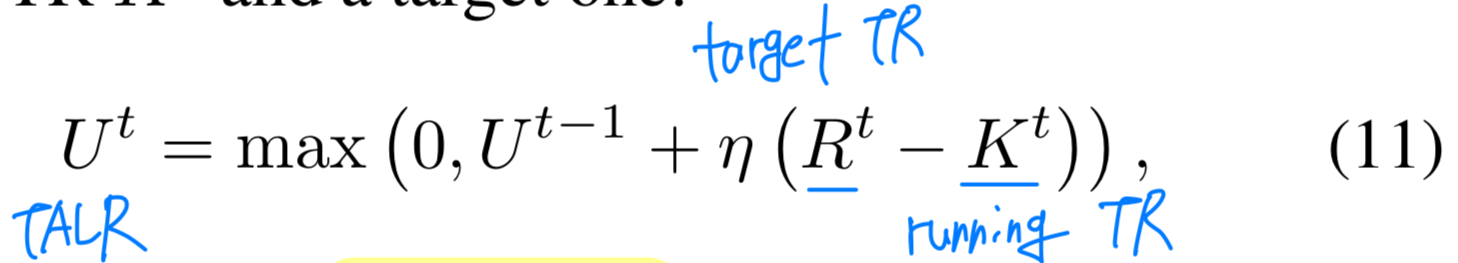      여기서 UtU^t는 iteration step tt에서의 TALR이고
      RtR^t는 iteration step tt에서의 target TR이다.
      η\eta는 TALR update의 크기를 조절하는 hyperparameter이다.
      Target TR RtR^t는 일반적인 scheduler (예: step decay)를 사용해 조정할 수 있으며, 이는 기존의 LR scheduling technique와 유사하다.
    2. updating latent weights
      이렇게 계산된 TALR UtU^t를 이용해 Latent weight wtw^t를 다음과 같이 update한다:
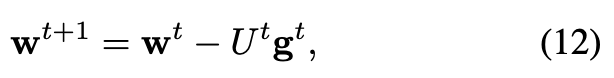      여기서 gtg^t는 사용되는 optimizer에 따라 계산되는 gradient term이다.
      TALR UtU^t를 통해 latent weight를 update함으로써,
      quantized weights의 running TR KtK^t를 target TR RtR^t에 맞게 제어할 수 있다.
      예를 들어, 현재 running TR KtK_t가 target TR RtR_t보다 작다면, Eq. (11)에 따라 TALR UtU_t가 증가하게 된다.
      그 결과 Eq. (12)에서 latent weight가 이전 iteration보다 더 크게 update되며,
      이는 더 많은 latent weight가 quantizer의 transition point를 통과할 수 있도록 유도한다.
      이에 따라 다음 iteration에서 TR이 증가하게 된다.
      반대로, KtK_t가 RtR_t보다 클 경우 TALR은 감소하여 TR은 줄어들게 된다.

정리하자면 아래 그림과 같음.
target TR RtR^t를 조절함에 따라 latent weight의 update 크기가 adaptive하게 결정되고,
그 결과 TR (transition 횟수) 또한 자연스럽게 많아짐.

4.3. Quantization scheme

Skip

5. Experiments

5.1. Experimental settings

5.2. Results

Image classification

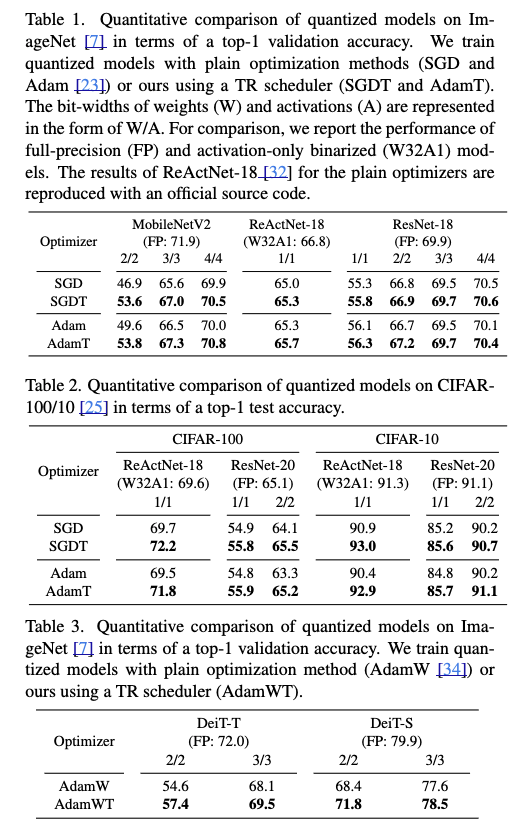
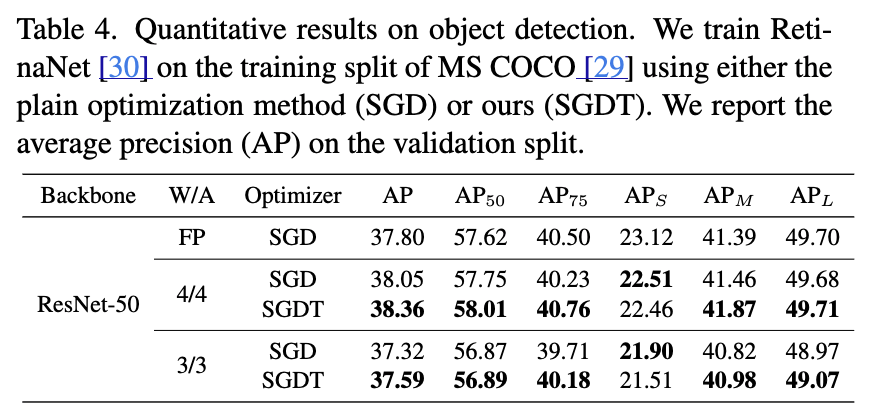
Object detection

5.3. Analysis

Topics discussed during the seminar

  1. QAT에서 full-precision latent weights를 없앨 수는 없는걸까?
    기존의 (1) latent weights, (2) quantized weights (latent weights quantized by quantizer)
    에서 (1)을 없애고 딱 quantized weights만 남기도록.
  1. 저자들이 설계한 TR scheduling은 PID(Proportional Integral Derivative) controller의 원리와 유사함.
    여기서, η\eta 값이 매우 민감하고 중요할텐데... η\eta 값은 hyperparameter로 작용함.
    사실상 Learning rate tuning하는 것과 동일한 hand-designed 요소임.
    →\to Hyper-parameter 의존도는 아직도 존재하는 한계로 생각됨.
  1. 저자들은 TR scheduling을 cosine annealing으로만 했음.
    과연 이 scheduling을 step function으로 했다면 결과가 어땠을까?
    TR scheduling에서 target TR이 step function에서는 1/10배 1/100배씩 크게 감소하므로,
    그 근방에서 feedback control이 불안정했다가 서서히 안정화될 것이라 생각이 드는데,
    이러한 실험도 같이 보여줬으면 더 좋았을 것 같다.
profile
Hyungseop Lee
Efficient Deep Learning
이전 포스트

[2020 ICLR] LEARNED STEP SIZE QUANTIZATION

0개의 댓글