[2020 ICLR] LEARNED STEP SIZE QUANTIZATION

Hyungseop Lee·2025년 3월 27일

[Paper Review] Model Compression - Quantization, etc

목록 보기
5/5

Paper Info.

https://arxiv.org/pdf/1902.08153

Absract

  • Deep networks는 inference 시 low precision operations을 사용하면
    high precision에 비해 power and space advantages를 제공하지만,
    precision이 낮아질수록 high accuracy를 유지하는 것이 challenge이다.

  • 본 논문에서는 이러한 (low precision operations) network의 training을 위한 방법인 Learned Step Size Quantization을 제안하며,
    이를 통해 다양한 architectures의 model에서 weights and activations을 2-, 3- or 4-bits로 quantize할 때
    ImageNet dataset에서 현재까지 highest acc를 달성했다.
    또한, 3-bit models을 학습하여 full precision baseline acc에 도달할 수 있었다.

  • 구체적으로,
    각각의 weight and activation layer의 quantizer step size에서 task loss gradient를 estimate하고 scale하는 새로운 방법을 도입하여,
    이를 network의 다른 parameters와 함께 학습할 수 있도록 한다.

    • quantizer step size란? 양자화(실수값을 정수값으로 변환)할 때 사용하는 간격을 의미.
      양자화는 일반적으로 다음과 같이 수행됨:
      Q(x)=clip(round(xs),qmin,qmax)×sQ(x)=clip(round(\frac{x}{s}), q_{min}, q_{max}) \times s
      (여기서 xx는 real value,
      ss는 step size,
      round(⋅)round(\cdot),
      Q(x)Q(x)는 quantized value,
      clip(z,qmin,qmax)clip(z, q_{min}, q_{max})는 값 zz를 qminq_{min} 이상, qmaxq_{max} 이하로 제한하는 함수이다.)
    • quantizer step size에 따라 quantized 결과가 달라질텐데, 그 step size를 학습한다는 아이디어인듯
  • 이는 기존 학습 코드에 간단한 수정만으로 적용이 가능하다.

1. Introduction

(background 및 related works 소개)

  • forward and backward 동안 high precision weights와 activations을 stochastic gradient descent를 통해 updaing함으로써,
    low precision networks가 trained될 수 있었다.

  • 우리는 task performance를 maximize하기 위해 each quantized layer를 mapping하고 싶은데,
    이거를 어떻게 optimally 달성할 수 있는지에 대한 질문은 여전히 남아있다.

    • 지금까지 대부분 a single step size parameter를 활용하여,
      uniform quantizers를 통해 low precision networks를 학습하고 있다.
    • 추가로, more complex nonuniform mappings이 고려되고 있다.
      (그림 출처)
      왼쪽 그림은 uniform quantization
      오른쪽 그림이 nonuniform quantization (예를 들어, 데이터 분포가 0에 몰려있는 경우 절대값이 작은 값들에 대해 더 세밀한 정보 표현을 위해 logarithmic quantization과 같은 nonuniform quantization을 사용함)
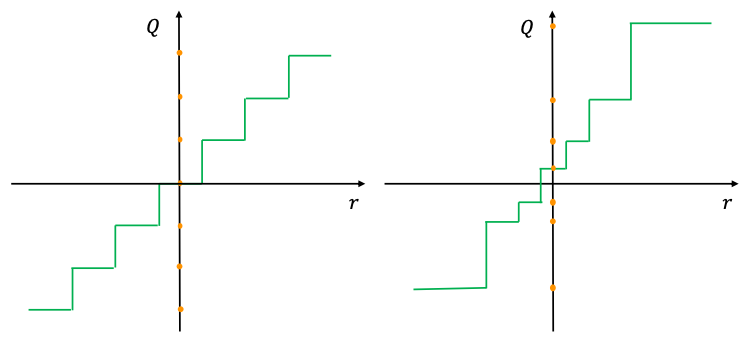
    • low precision deep networks는 a simple fixed configuration for the quantizer를 사용했다.
    • 이후에는 data에 fitting하거나 data distribution의 statistics에 기반한 quantizer에 집중했다.
    • 또는 training 동안에 quantization error를 minimze하는 방법을 찾았다.
    • 가장 최근에는, task loss를 minimizes하는 a quantizer를 학습하기 위해 SGD로 backpropagation을 사용하는 데에 초점을 맞추고 있다.

(문제 제기)

  • 그들의 simplicity의 매력에도 불구하고, user settings에 기인한 fixed mapping schemes는
    network performance를 optimizing한다는 보장을 제공하지 않는다.
    또한, quantization error를 minimization schemes은 quantization error를 perfectly optimize할 수는 있지만,
    다른 quantization mapping이 실제로 task error를 minimize한다면 still be not optimal이다.
    (해석: quantization error를 minimization하는 방법은 딥러닝 관점이 아니라 정보이론? 관점에서 정말 숫자의 정보 손실을 최소화하는 방향으로 변환하는 것이지만, 딥러닝 관점에서 양자화는 실제값이 갖고 있는 정보가 손실되더라도 전체 task error를 minimize하는 것이 목표가 되어야 한다.)

  • 우리는 quantization mapping을 학습하여 task loss를 minimize하는 방법에 주목하는데, 이는 우리가 관심을 가지는 주요 metric를 직접적으로 향상시키려는 접근 방식이기 때문이다.
    하지만, quantizer는 그 자체로 discontinuous하므로, 이러한 접근 방식에서는 gradient를 approximating하는 것이 필요하다.
    기존 연구들은 이를 상대적으로 coarse manner (거친 방식)으로 다루었으며, quantized states 간 transition의 impact는 무시했다.

    • quantizer가 discontinuous하다는 것은 뭐고, 왜 gradient를 approximating해야 할까?
      입력 값 (real value)에 아주 작은 변화가 생기면 출력 값 (quantized value)이 갑자기 크게 변함.
      그래서 대부분의 구간에서 gradient는 0 이거나 정의되지 않는다.
      이렇게 되면, step size를 어떻게 update해야 loss가 줄어드는지에 대한 정보를 얻을 수 없다.
      따라서, discontinuous quantizer를 통과하는 동안 gradient가 "흐르도록"하기 위해 gradient를 approximating하는 방법이 필요하다.
      이 논문에서 언급하는 "straight through estimator (STE)"는 대표적인 gradient approximate 방법 중 하나이다.

(제안)

  • 여기서, 우리는 deep network의 각 layer에 대해 quantization mapping을 학습하는 새로운 방법인 Learned Step Size Quantization (LSQ)를 소개하며,
    기존 연구보다 two key contributions을 제시한다.

    1. 우리는 quantized state transitions에 sensitive하게 반응하여, step size의 gradient를 approximate하는 a simple way를 제시한다.
      이를 통해, step size를 model parameter로써 학습할 때 finer grained optimization (더 정밀한 최적화)가 가능하다.

    2. step size updates의 magnitude (크기)가 weight updates의 magnitude와 더 잘 균형을 이루도록 하는 a simple heuristic을 제안하며,
      이를 통해 convergence가 개선되었다.

2. Method

(notation)

  • vv는 real value
    ss는 quantizer step size
    QPQ_P는 #positive quantization levels
    QNQ_N는 #negative quantization levels
    vˉ\bar{v}는 a quantized and integer scaled representation of the data (vv)
    v^\hat{v}는 a quantized representation of the data at the same scale as vv
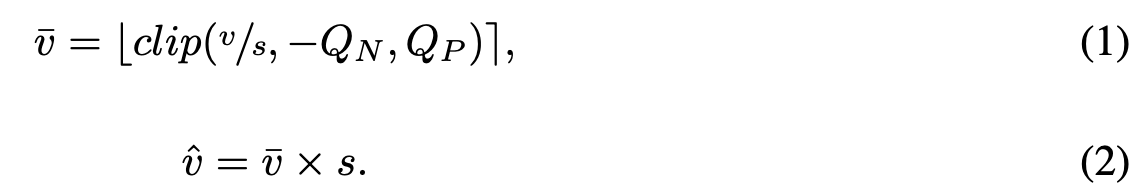    여기서,
    clip(z,r1,r2)clip(z, r_1, r_2)은 r1r_1 이하 값들은 r1r_1, r2r_2 이상 값들은 r2r_2로 return
    ⌊z⌉\lfloor z \rceil는 zz를 the nearest integer로 return
    bb bits로 encoding한다고 가정했을 때,
    unsigned data (activations) QN=0Q_N=0이고 QP=2b−1Q_P=2^b-1 (2-bit 양자화면, 0 3)
    signed data (weights) QN=−2b−1Q_N=-2^{b-1}이고 QP=2b−1−1Q_P=2^{b-1}-1 (2-bit 양자화면, -2 1)

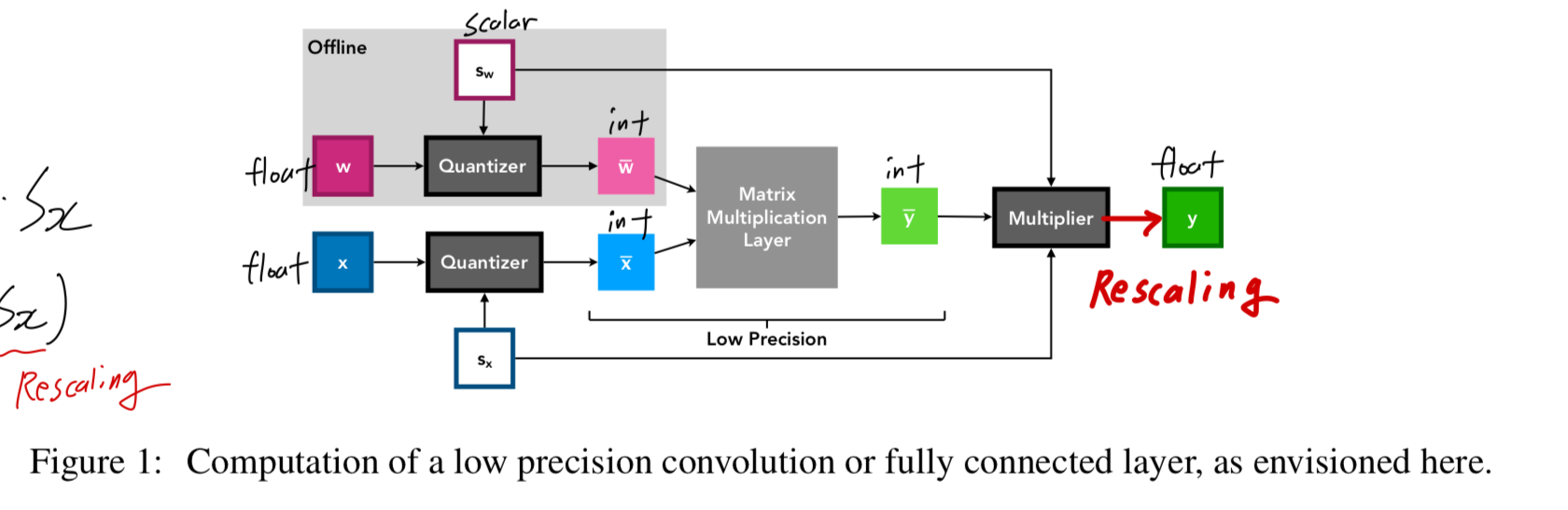
  • inference 동안에,
    wˉ\bar{w}와 xˉ\bar{x} values는 low precision integer matrix multiplication units의 input으로 사용될 수 있다.
    그 후, 이러한 layer의 output을 step size를 사용하여 rescaling하는데,
    이는 상대적으로 low cost인 high precision scalar-tensor multiplication 연산으로 수행될 수 있다.
    또한, 이 과정은 batch normalization 등의 다른 연산과 algebraically merged (대수적으로 병합)될 가능성이 있다.

2.1. Step Size Gradient

  • LSQ는 다음과 같은 gradient를 quantizer를 통해 step size parameter로 전달함으로써,
    training loss에 기반하여 ss를 학습할 수 있는 방법을 제공한다.

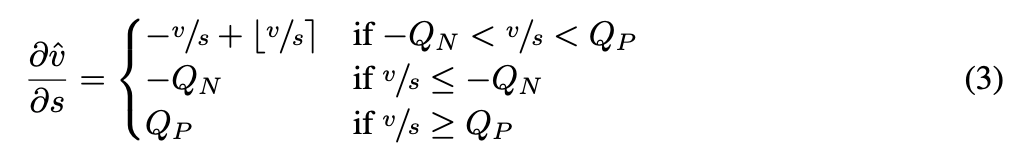
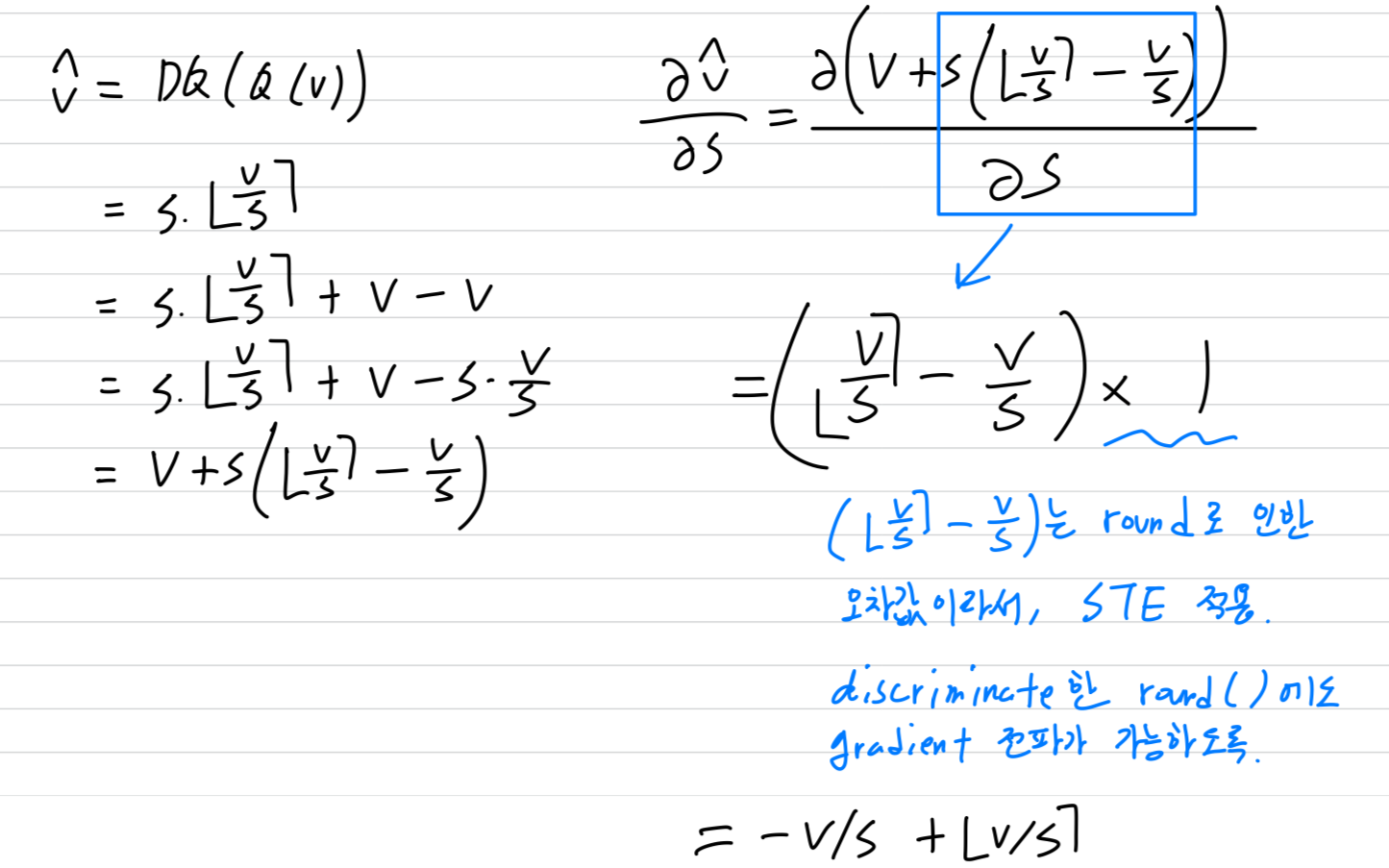
  • 이 gradient는 straight-through estimator (STE)를 사용하여
    round function의 gradient를 pass-through operation으로 근사함으로써 유도    된다.
    즉, round operations을 그대로 유지하여 후속 연산들의 미분 과정에는 영향을 주지 않도록 하면서, 나머지 모든 연산 (Eq 1과 Eq 2)은 정상적으로 미분한다.

  • 이 gradient는 기존의 approximations들과는 차이가 있다. (Figure 2)

    • QIL (Jung et al., 2018)은 discretization (양자화?) 이전에 data의 transformation을 학습하는 방식을 사용했다.
    • PACT (Choi et al., 2018b;a)는 round 연산을 forward 식에서 제거하고, 대수적으로 항을 소거한 후 미분하여 특정 구간 −QN<v/s<QP-Q_N < v/s < Q_P에서 ∂v^∂s=0\frac{\partial{\hat{v}}}{\partial{s}}=0이 되도록 만드는 방식을 사용했다.

  • QIL, PACT 두 연구에서는, vv가 양자화된 상태 간 transition point에 얼마나 가까운지가 quantization parameters의 gradient에 영향을 주지 않는다.
    하지만 직관적으로 보면, vv가 a quantization transition point에 가까울수록,
    ss가 조금만 변해도 quantization bin (vˉ\bar{v})가 바뀌기 쉽고,
    그 결과 a large jump in v^\hat{v}를 만든다.
    따라서, vv가 transition point 경계에 가까울수록 ∂v^∂s\frac{\partial{\hat{v}}}{\partial{s}}값이 커질 것으로 예상되며, 실제로 LSQ gradient에서 이러한 관계를 관찰할 수 있다.
    이 gradient는 our simple quantizer formulation과 round function에 대한 STE 적용만으로 자엽스럽게 도출된다.

  • 이 연구에서는, 각 weights layer와 activations layer마다 서로 다른 step size를 사용하며, 이는 fp32 value로 표현된다.
    step size 초기화는 2<∣v∣>QP\frac{2<|v|>}{\sqrt{Q_P}}로 되는데,
    여기서 vv는 weights 또는 activations을 나타내며,
    weights는 the initial weights values을 기반으로,
    activations은 the first batch of activations을 기반으로 계산된다.

2.2. Step Size Gradient Scale

  • training 동안에 network의 all weight layers에서 average update 크기와 average parameter 크기의 비율이 대략 동일할 때
    good convergence를 보인다는 것이 입증    되었다.
    learning rate가 적절하게 설정되면, 이는 모든 udpate가 너무 커서 local minima를 overshooting하는 경우를 방지하고,
    반대로 너무 작아서 불필요하게 long convergence time을 초래하는 경우를 방지하는 데 도움을 준다.

  • 이와 같은 개념을 확장하여, 각 step size 역시 weight와 유사한 ratio로 update 크기와 parameter가 조정되어야 한다고 가정한다.
    따라서, 어떤 loss function LL에 대해 훈련된 network에서 다음의 ratio가 평균적으로 1에 가까워야 한다.
    그러나 precision이 증가할수록 (즉, data가 더 세밀하게 양자화될수록) step size parameter는 더 작아질 것으로 예상되며,
    반대로 양자화된 항목의 개수가 많아질수록 (즉, gradient를 계산할 때 더 많은 items들이 합산됨) step size updates는 더 커질 것으로 예상    된다. (?)
    (precision이 높다는건 더 촘촘하게 표현해야 하므로 step size가 작아질 것이라는 뜻인듯)
    이를 보정하기 위해, gradient of step size에는 gradient scale gg를 곱해준다.
    weight step size를 위한 g=1NWQPg=\frac{1}{\sqrt{N_WQ_P}}, activation step size를 위한 g=1NFQPg=\frac{1}{\sqrt{N_FQ_P}}를 곱해준다.
    NWN_W는 #weights in a layer
    NfN_f는 #features in a layer 이다.

3. Results

내가 이해한 내용, 기여

기존에는 step size를 수동으로 정해 task performance를 minimize하는게 아니라 정보이론의 측면에서 정보 손실을 최소화하는 방향으로 연구가 되었는데,
여기서의 양자화는 task performance minimize로 목표로 하여 step size가 network의 loss를 최소화할 수 있도록 SGD를 통해 학습 가능하게 만듦.
그래서 step size에 대한 gradient를 정의함.
정의하는 과정에서 round() 함수에 의해 생기는 transition point에 대한 vv의 민감도를 고려하는 gradient를 정의함.

profile
Hyungseop Lee
Efficient Deep Learning
이전 포스트

[ICML 2017] How Do Adam and Training Strategies Help BNNs Optimization?

0개의 댓글