DETR variants들의 흐름과 해당 논문들에 대한 내용을 요약
DETR
-
object detection은 object의 (bounding box, category label)이라는 set을 예측하는 것.
이전의 object detector들은 이러한 set prediction task를 간접적으로 다룸.
간접적으로 다룬다?
➡️ large set of proposal, anchors, or window centers에 대한 regression 및 classification 문제를 정의함으로써 set prediction이 이루어짐.
➡️ 따라서 object detection의 성능은 post-processing(NMS), anchor set 설계, target box를 anchor에 할당하는 heuristic에 의해 크게 영향을 받음. -
위와 같은 문제를 해결하기 위해 DETR은 Transformer encoder-decoder architecture를 이용한
direct set prediction approach를 제안하여 training pipeline을 간소화함.
➡️ 즉, anchor or NMS와 같은 hand-designed 요소들을 제거함으로써 detection pipeline을 간소화함. -
DETR의 direct set prediction을 위한 두가지 주요 구성이 있다.
- a set prediction loss that forces unique matching between predicted and ground truth boxes
(set prediction loss는 predicted box와 GT box가 중복 없이 1:1 matching을 할 수 있도록 학습된다) - an architecture that predicts(in a single pass) a set of object and models their relation.
- a set prediction loss that forces unique matching between predicted and ground truth boxes
3.1. Object detection set prediction loss
-
training시에 loss는 predicted box와 GT box 간의 optimal bipartite matching을 만들어내고,
object-specific losses를 optimize한다.
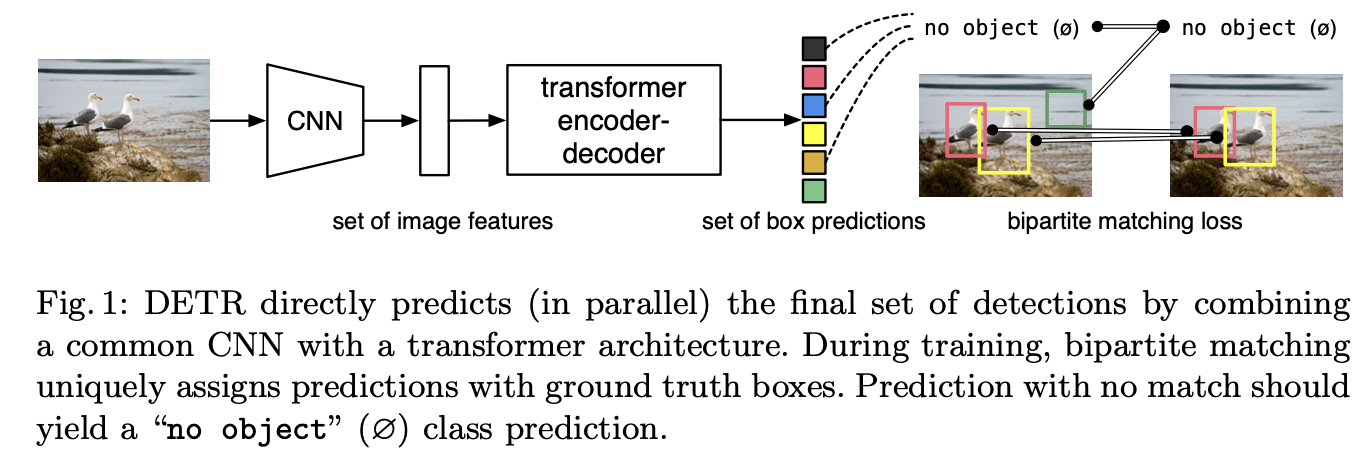
- bipartite matching(이분 매칭)이란?
training 과정에서 predicted box와 GT box를 1:1 matching하여,
같은 object를 중복 prediction하지 않도록 한다.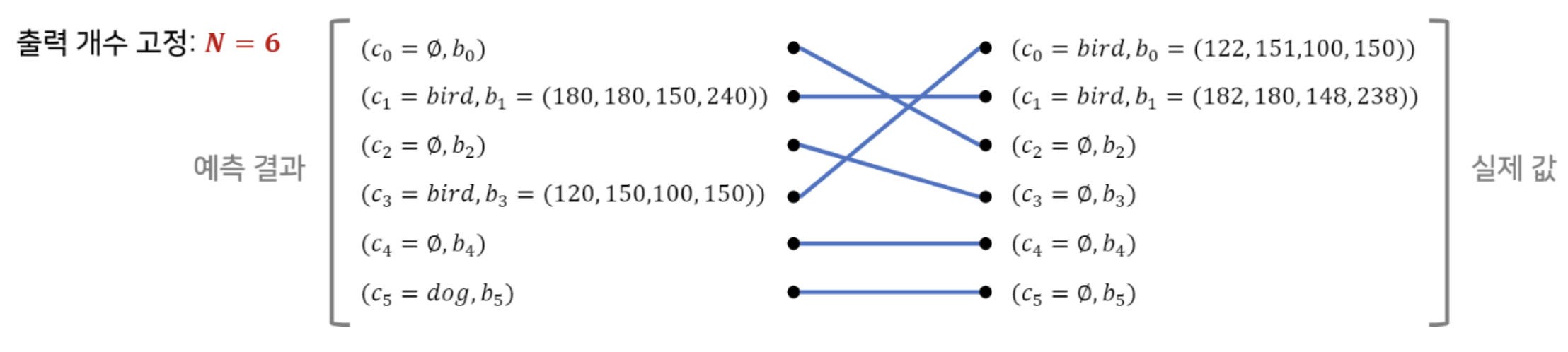 DETR은 decoder의 single pass를 통해 fixed-size 개의 prediction set을 출력함.
DETR은 decoder의 single pass를 통해 fixed-size 개의 prediction set을 출력함.
은 한 image에서 일반적으로 가지는 object의 개수보다 큰 값으로 설정함.
(예를 들어, coco2017 dataset에서 한 image에 object 개수가 가장 많은 image가 11개라고 가정했을 때,
은 11 이상의 값으로 설정해야 함. 그래야 bipartite matching이 가능해지기 때문) - bipartite matching은 hungarian algorithm으로 효율적으로 계산될 수 있다.
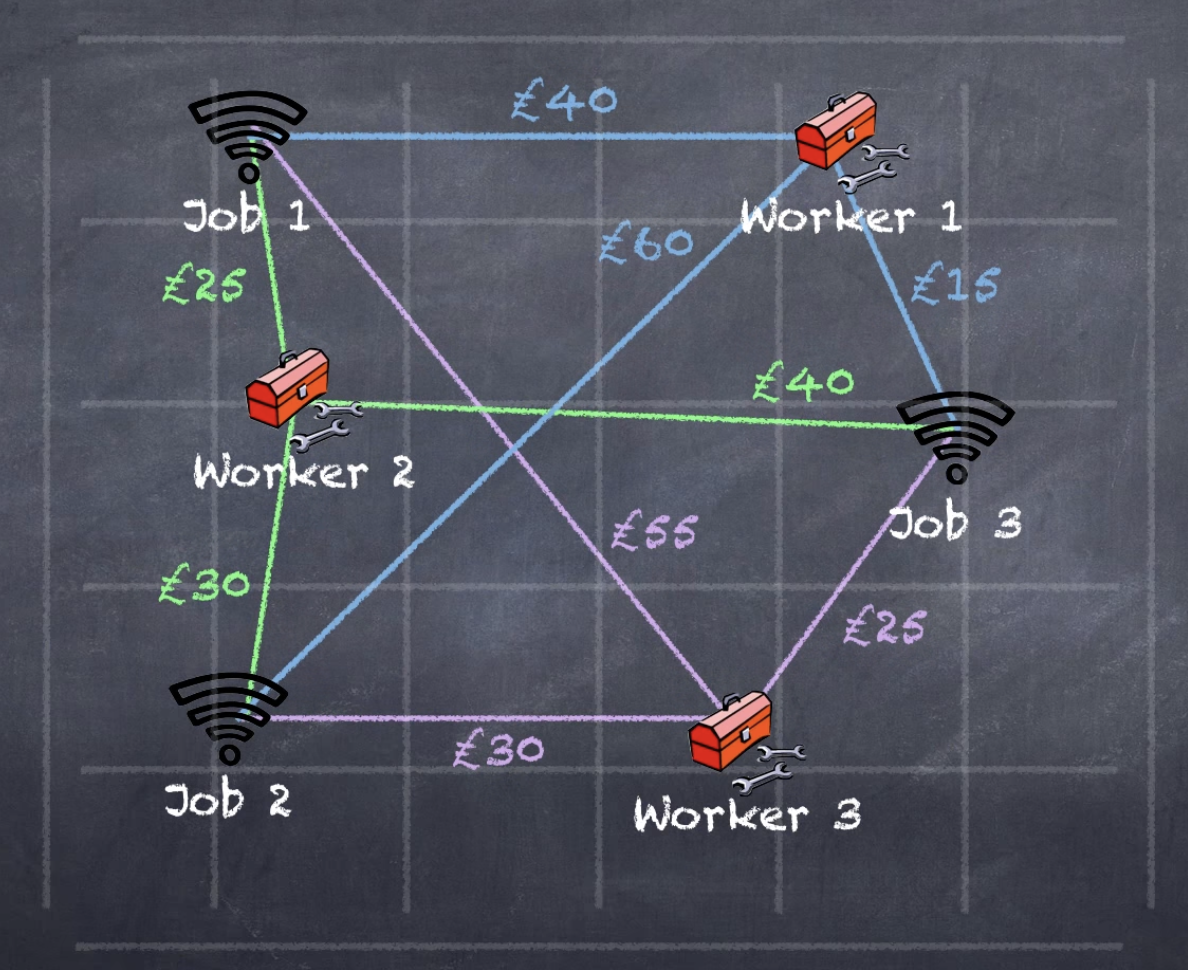 어떤 worker를 어떤 Job에 할당시켜야 cost를 최소화할 수 있는지 계산하는 algorithm.
어떤 worker를 어떤 Job에 할당시켜야 cost를 최소화할 수 있는지 계산하는 algorithm. (알고리즘 설명 참고 : https://www.youtube.com/watch?v=cQ5MsiGaDY8&t=309s)
(알고리즘 설명 참고 : https://www.youtube.com/watch?v=cQ5MsiGaDY8&t=309s)
- hungarian algorithm으로 optimal bipartite matching을 완료.
이때, optimal matching을 라고 하자.
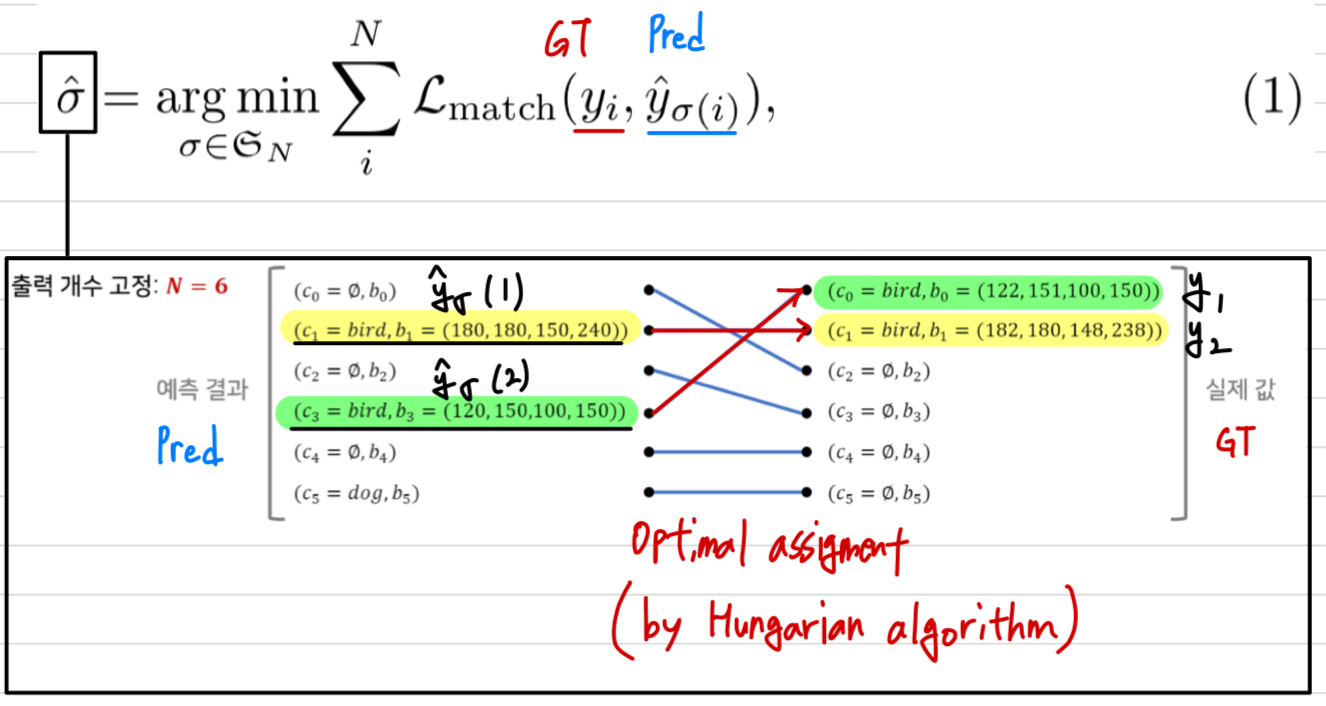
- 이제 hungarian algorithm으로 찾은 optimal matching()에 대한 loss를 구해야 함.
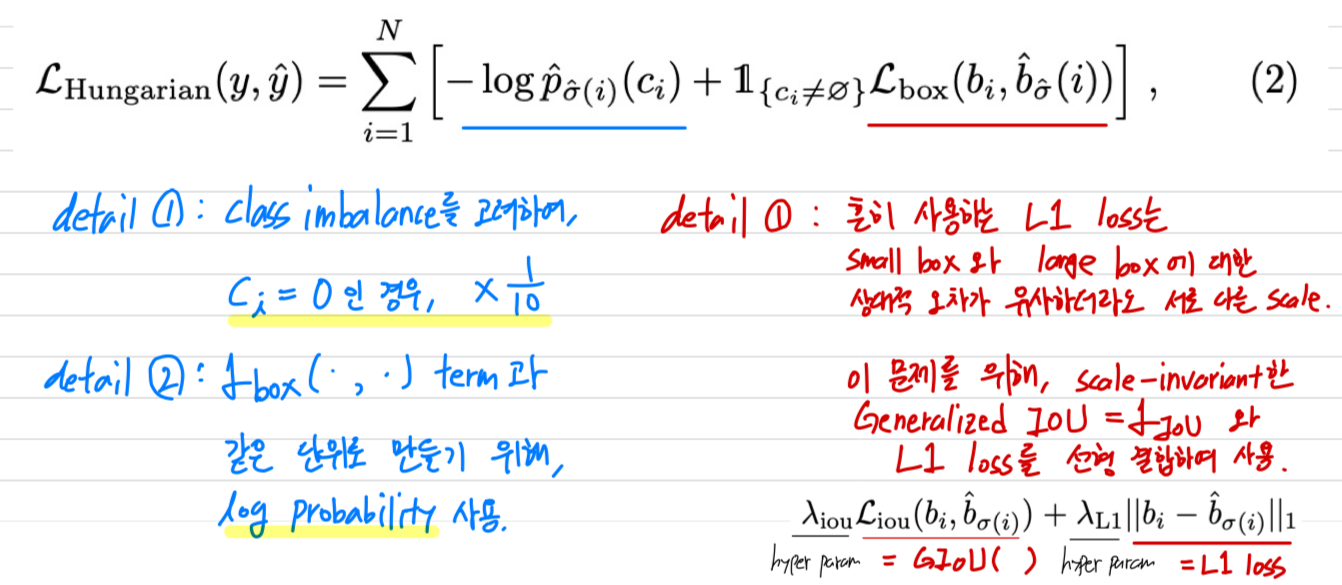
- bipartite matching(이분 매칭)이란?
-
논문에서는 위에서처럼
step 1) hungarian algorithm을 사용해서 optimal assignment()을 찾고나서,
step 2) 해당 assignment에 대한 loss만을 구했는데
하지만 코드를 분석해보니,
실제 구현에서는 hungarian algorithm을 사용할 때 만들어지는 cost matrix가 loss값들임.
다시 말해,
step 1) 각각의 matching 경우의 수(N=100)에 대한 loss값을 전부 구함.
N=100이지만 GT box 개수에
step 2) step1의 loss값으로 cost matrix를 만들어 hungarian algorithm을 수행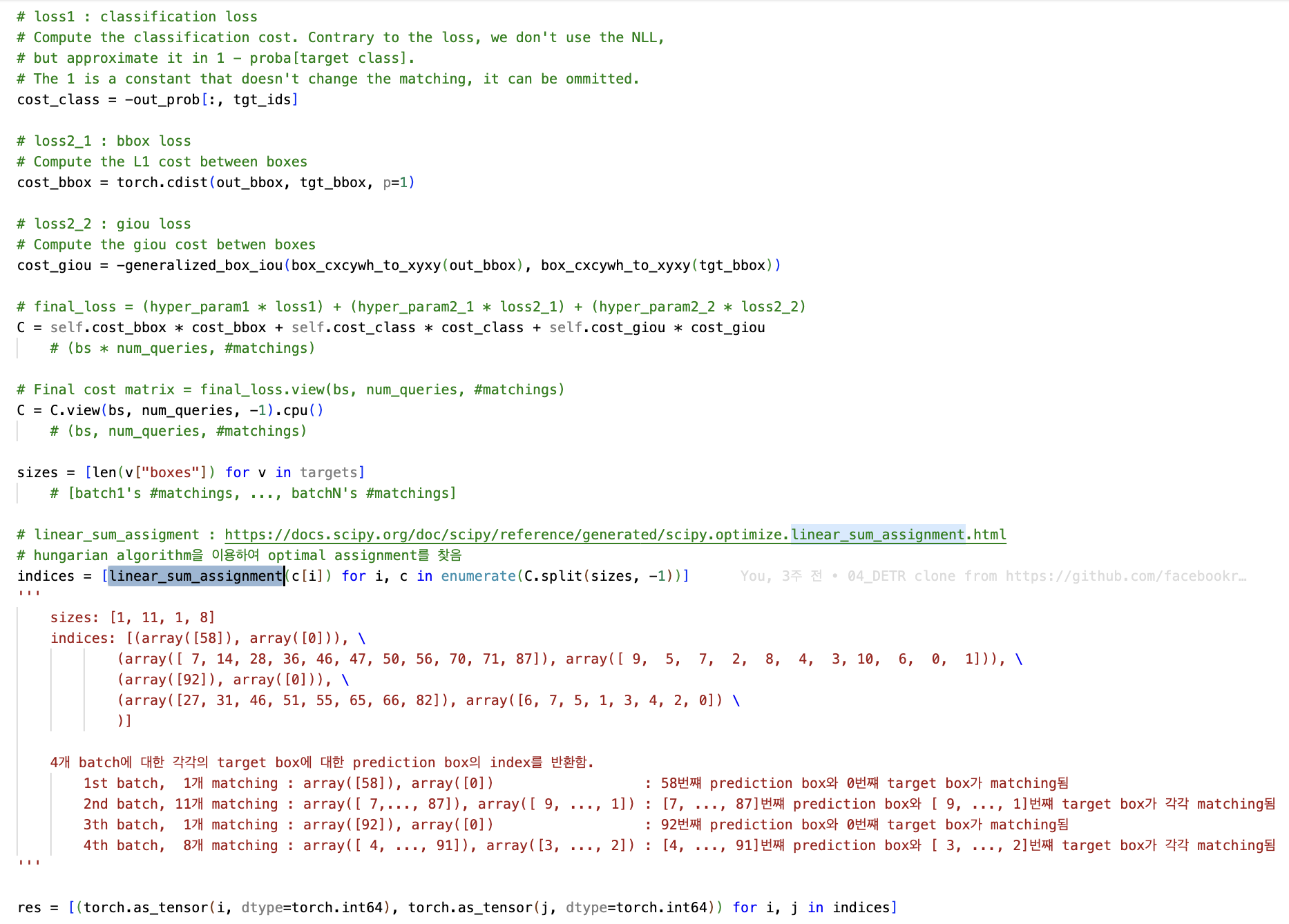
-
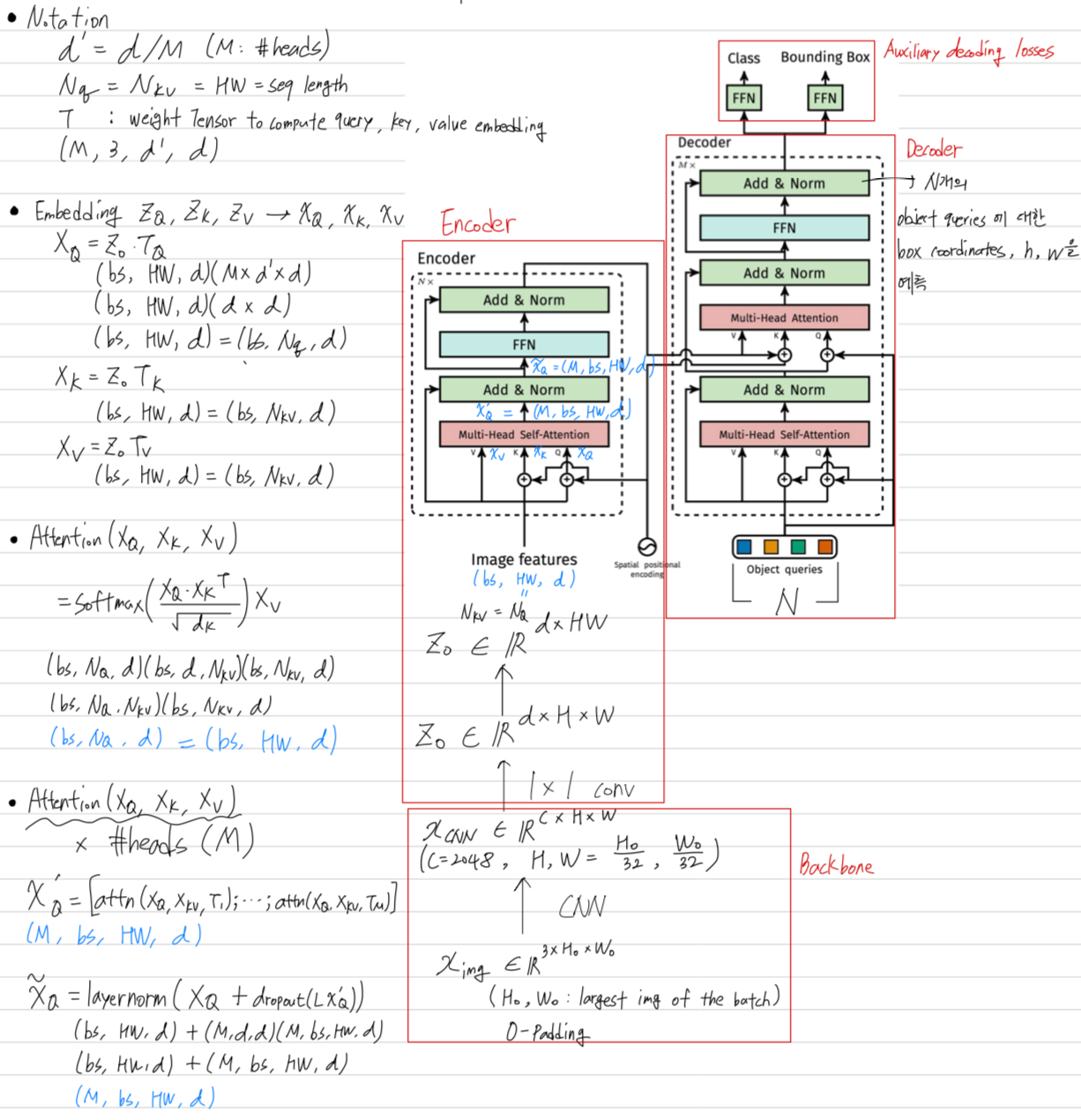
그림으로 간단하게 요약하자면,
다음과 같이 CNN backbone을 거친 image feature가 transformer의 encoder-decoder architecture에 들어가게 되고,
코드에서는 default로 num_queries=100이었으니, 100개의 object queries가 decoder에 입력된다. 따라서 100개의 set of box predictions이 생성이 되는데,
따라서 100개의 set of box predictions이 생성이 되는데,
100개의 box prediction과 (e.g.)2개의 GT box와의 hungarian algorithm을 통해
bipartite matching을 진행하여 최종 2개의 set of box predictions이 matching되어
해당하는 matching에 대한 loss로 parameter를 update함.

3.2 DETR architecture
paper with code
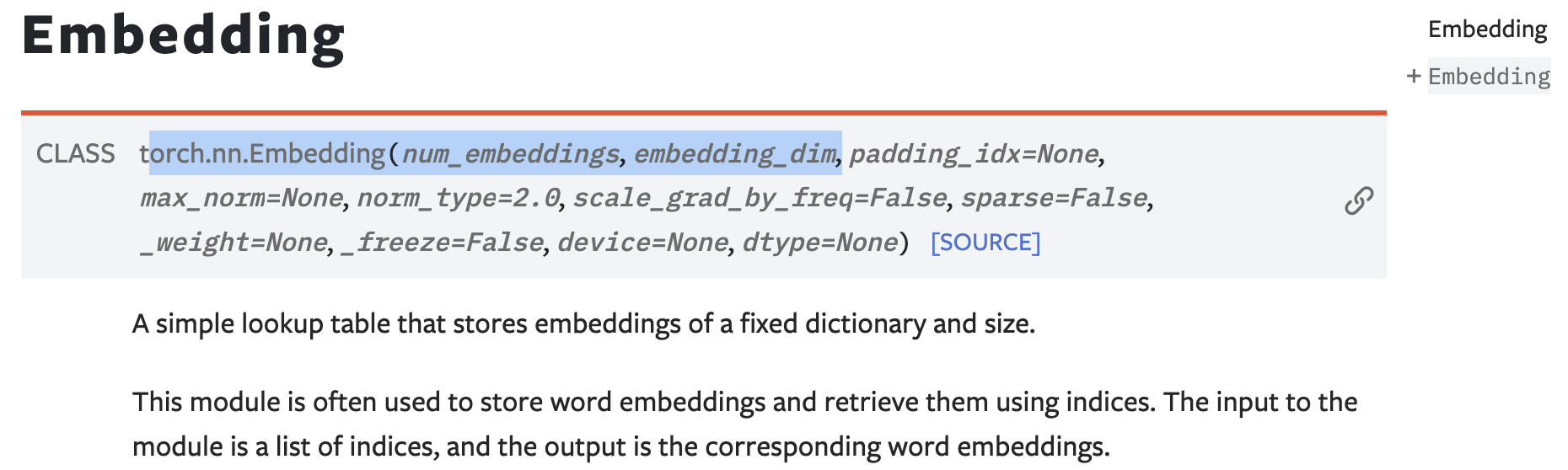
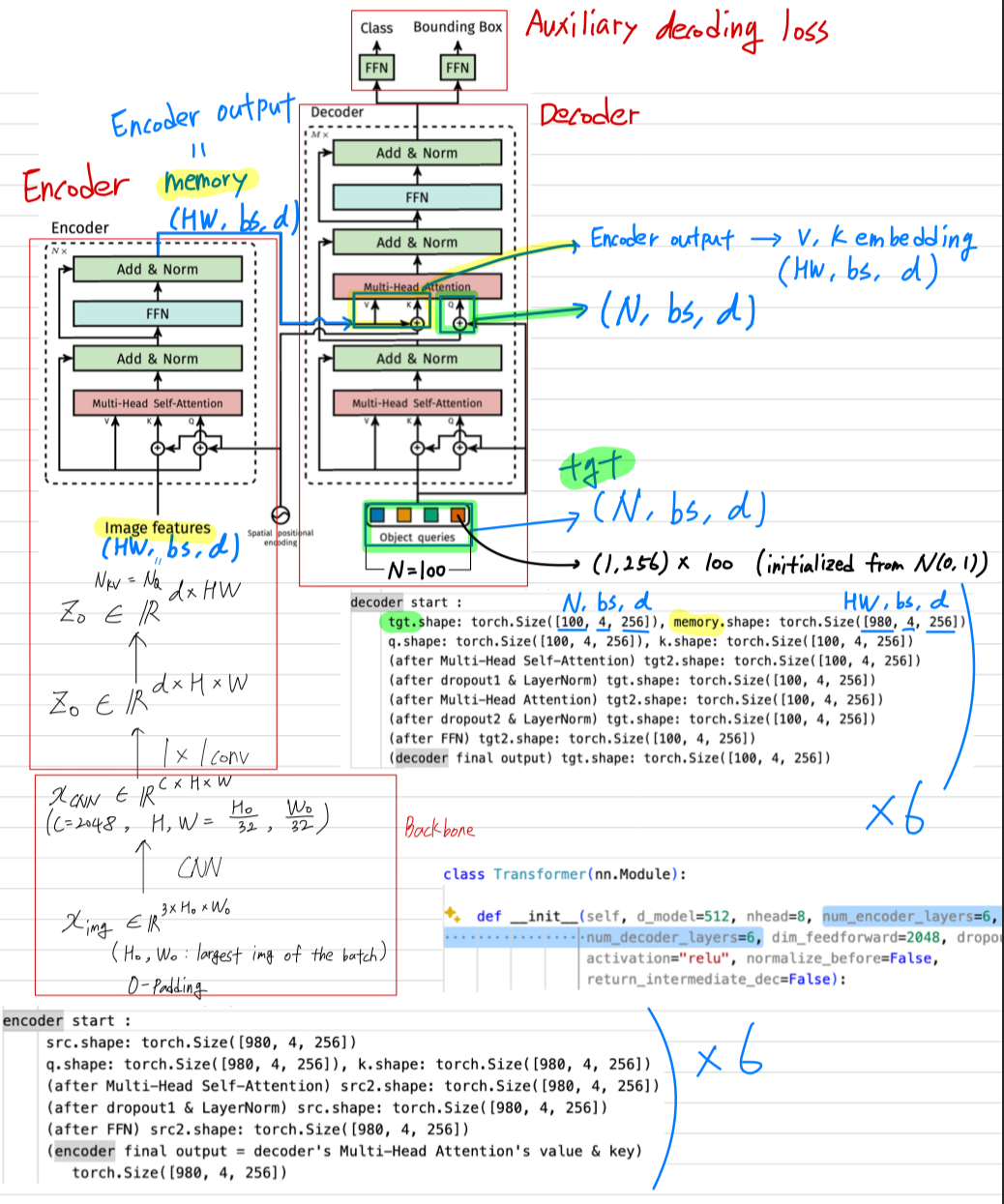 Object queries는 로 initialization되는 learnable parameter이다.
Object queries는 로 initialization되는 learnable parameter이다.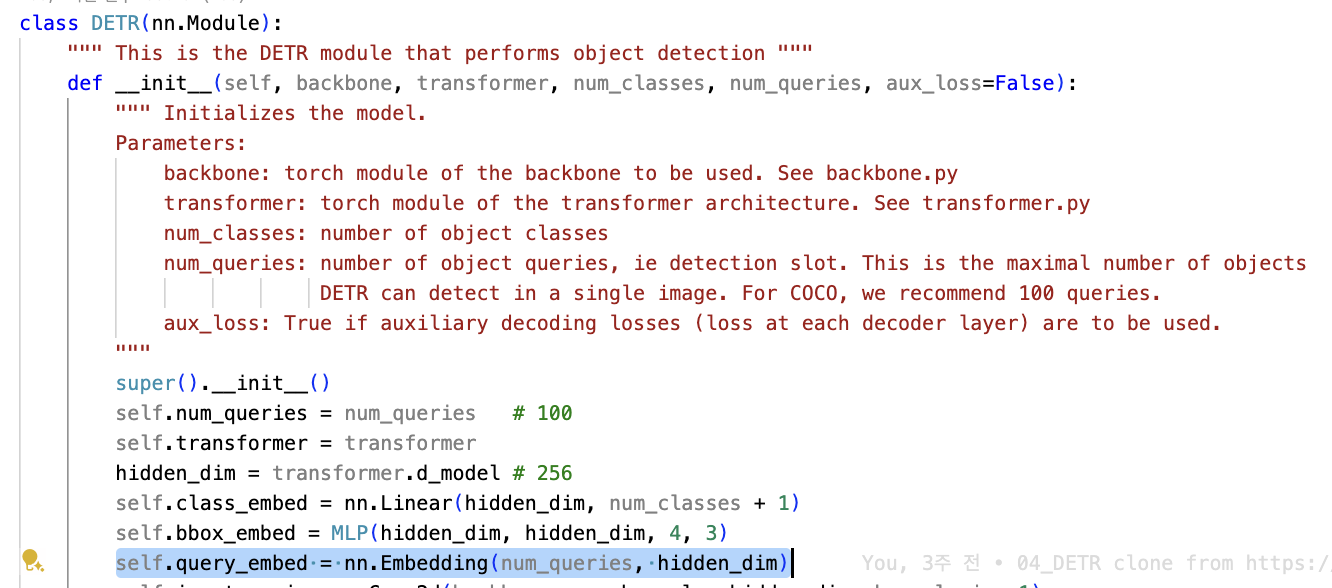
 + auxiliary decoding loss를 추가한 이유는 올바른 object 수를 출력하는 데에 도움이 되었다고 함
+ auxiliary decoding loss를 추가한 이유는 올바른 object 수를 출력하는 데에 도움이 되었다고 함
- encoder forward
# src : image features (HW, batch_size, hidden_dim)
def forward_post(self,
src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
print(f"encoder start :")
print(f"\t src.shape: {src.shape}")
'''
src : image features
(HW, batch_size, hidden_dim = 256)
'''
q = k = self.with_pos_embed(src, pos)
print(f"\t q.shape: {q.shape}, k.shape: {k.shape}")
'''
q : query
(HW, batch_size, hidden_dim = 256)
k : key
'''
src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
'''
src2 : Multi-Head Self-Attention output
(HW, batch_size, hidden_dim = 256)
'''
print(f"\t (after Multi-Head Self-Attention) src2.shape: {src2.shape}")
src = src + self.dropout1(src2)
src = self.norm1(src)
'''
src : dropout(+Add) & LayerNorm
(HW, batch_size, hidden_dim = 256)
'''
print(f"\t (after dropout1 & LayerNorm) src.shape: {src.shape}")
src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
'''
src2 : FFN output
src :
(HW, batch_size, hidden_dim = 256)
-> linear1 : (hidden_dim = 256, dim_forward = 2048)
(HW, batch_size, dim_forward = 2048)
-> linear2 : (dim_forward = 2048, hidden_dim = 256)
(HW, batch_size, hidden_dim = 256)
'''
print(f"\t (after FFN) src2.shape: {src2.shape}")
src = src + self.dropout2(src2)
src = self.norm2(src)
print(f"\t (encoder final output = decoder's Multi-Head Attention's value & key)")
print(f"\t\t{src.shape}")
return src- decoder forward
# tgt : object queries, memory : encoder output
def forward_post(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
print(f"decoder start :")
print(f"\t tgt.shape: {tgt.shape}, memory.shape: {memory.shape}")
'''
tgt : object queries
(num_queries = 100, batch_size, hidden_dim = 256)
memory : encoder output
(HW, batch_size, hidden_dim = 256)
'''
# query, key + positional embedding
q = k = self.with_pos_embed(tgt, query_pos)
print(f"\t q.shape: {q.shape}, k.shape: {k.shape}")
'''
q : query
(num_queries = 100, batch_size, hidden_dim = 256)
k : key
(num_queries = 100, batch_size, hidden_dim = 256)
'''
# Multi-Head Self-Attention
tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
print(f"\t (after Multi-Head Self-Attention) tgt2.shape: {tgt2.shape}")
'''
tgt2 : Multi-Head Self-Attention output
(num_queries = 100, batch_size, hidden_dim = 256)
'''
# dropout(+Add) & Norm 1
tgt = tgt + self.dropout1(tgt2)
tgt = self.norm1(tgt)
print(f"\t (after dropout1 & LayerNorm) tgt.shape: {tgt.shape}")
'''
tgt : dropout(+Add) & LayerNorm
(num_queries = 100, batch_size, hidden_dim = 256)
'''
# Multi-Head Attention = Cross-Attention (encoder output = memory, decoder output = tgt)
tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
key=self.with_pos_embed(memory, pos),
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
print(f"\t (after Multi-Head Attention) tgt2.shape: {tgt2.shape}")
'''
tgt2 : Multi-Head Attention output
(num_queries = 100, batch_size, hidden_dim = 256)
'''
# dropout(+Add) & Norm 2
tgt = tgt + self.dropout2(tgt2)
tgt = self.norm2(tgt)
print(f"\t (after dropout2 & LayerNorm) tgt.shape: {tgt.shape}")
'''
tgt : dropout(+Add) & LayerNorm
(num_queries = 100, batch_size, hidden_dim = 256)
'''
# FFN
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
print(f"\t (after FFN) tgt2.shape: {tgt2.shape}")
'''
tgt2 : FFN output
tgt :
(num_queries = 100, batch_size, hidden_dim = 256)
-> linear1 : (hidden_dim = 256, dim_forward = 2048)
(num_queries = 100, batch_size, dim_forward = 2048)
-> linear2 : (dim_forward = 2048, hidden_dim = 256)
(num_queries = 100, batch_size, hidden_dim = 256)
'''
# dropout(+Add) & Norm 3
tgt = tgt + self.dropout3(tgt2)
tgt = self.norm3(tgt)
print(f"\t (decoder final output) tgt.shape: {tgt.shape}")
'''
tgt : dropout(+Add) & LayerNorm
(num_queries = 100, batch_size, hidden_dim = 256)
= decoder output
'''
return tgt

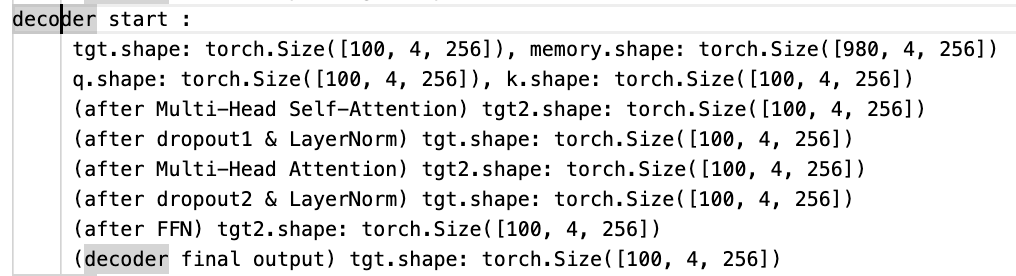
최종적으로 decoder output에 class_embed와 bbox_embed 연산을 적용하여
classification과 bbox를 prediction함.


Deformable DETR
- Deformable DETR에서는 DETR의 치명적인 두가지 단점을 지적.
- It requires much longer training epochs to converge than the existing object detectors.
- DETR delivers relatively low performance at detection small objects.
현대 object detector들은 high-resolution feature map으로부터 small objects를 detection하기 위해 multi-scale features를 사용한다.
하지만, DETR에 high-resolution feature maps을 사용하는 것은 unacceptable complexity를 유발한다.
-
위 두가지 문제점은 image feature maps을 처리하는 Transformer components의 결함에 기인한다.
- initialization할 때, attention module은 image feature map의 모든 pixel에 균일한 weight를 적용한다.
➡️ attention weight가 sparse meaningful location에 집중하도록 학습되기 위해서는 긴 training epoch이 필요하다. - Transformer encoder에서 attention weights computation은
pixel 수에 대해 quadratic computation을 요한다.
따라서 high-resolution feature maps을 처리하는 것은 매우 높은 computational and memory complexities를 갖는다.- (내가 이해한 내용)
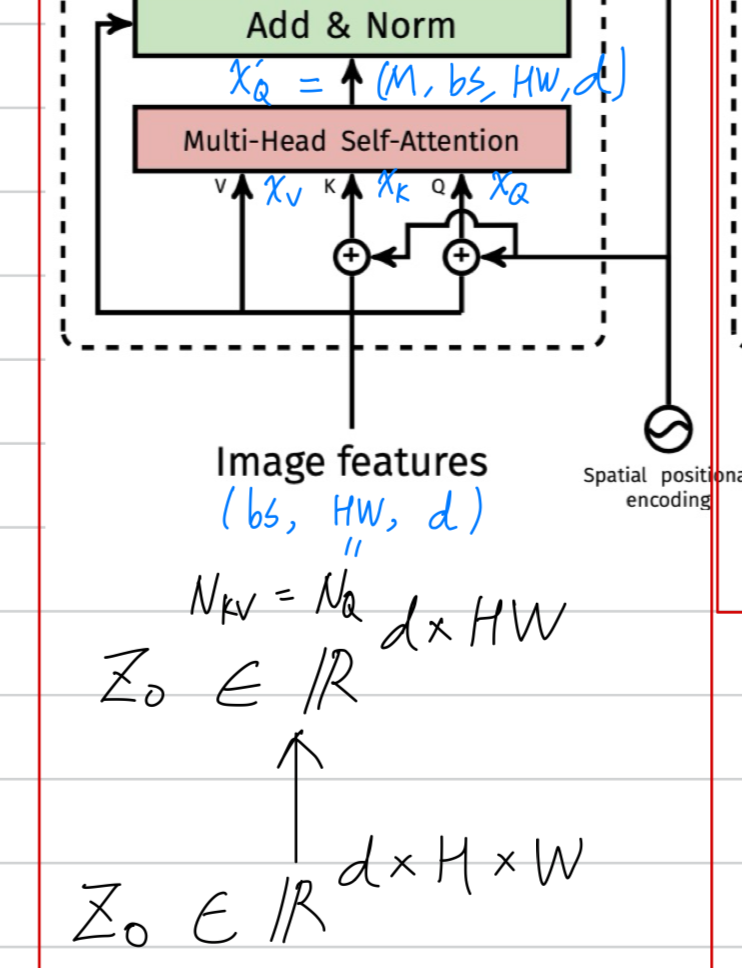 간략화하여, batch_size 차원을 빼면 아래 그림에서 다음과 같다.
간략화하여, batch_size 차원을 빼면 아래 그림에서 다음과 같다.
attention value를 얻기 위해서 중간에 tensor가 만들어진다.
만약 high-resolution feature maps에 대한 self-attention이었다면 이는 pixel 수에 대해 quadratic computation을 요하기 때문에
높은 computational complexities(초록 형광)와
memory complexities(노란 형광)를 갖게 될 것이다.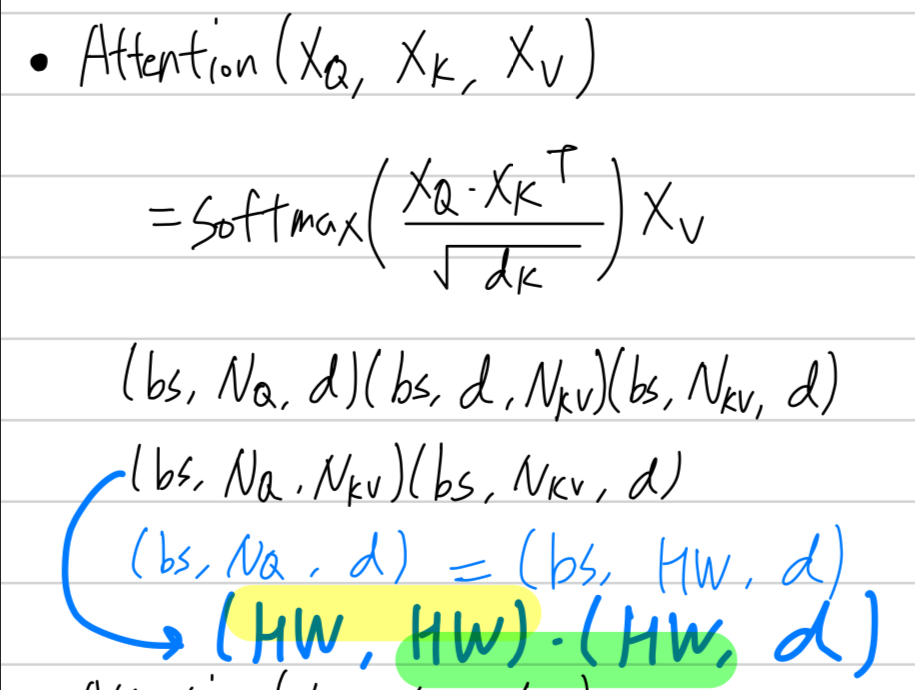
- (내가 이해한 내용)
- initialization할 때, attention module은 image feature map의 모든 pixel에 균일한 weight를 적용한다.
-
DETR의 위 두가지 문제를 해결하기 위해서 우리는 deformable convolution의 아이디어를 빌렸다.
image domain에서, deformable convolution은
sparse spatial location(sparse한 위치 정보)에 집중할 수 있는 강력하고 효율적인 mechanism이어서,
앞서 말한 DETR의 문제들을 자연스럽게 해결할 수 있다.- deformable convolution이란?
- 원래의 receptive field에 대해 conv layer를 거쳐, 의 offsets map을 얻어냄.
- input feature map의 해당 point에서 offset에 대해 일반적인 convolution 진행.
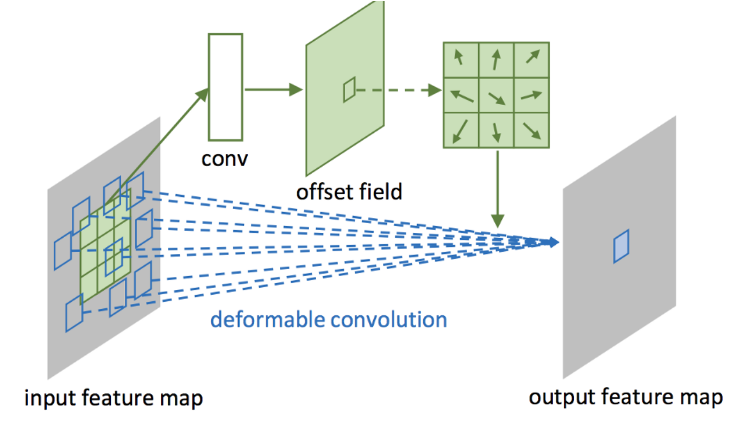
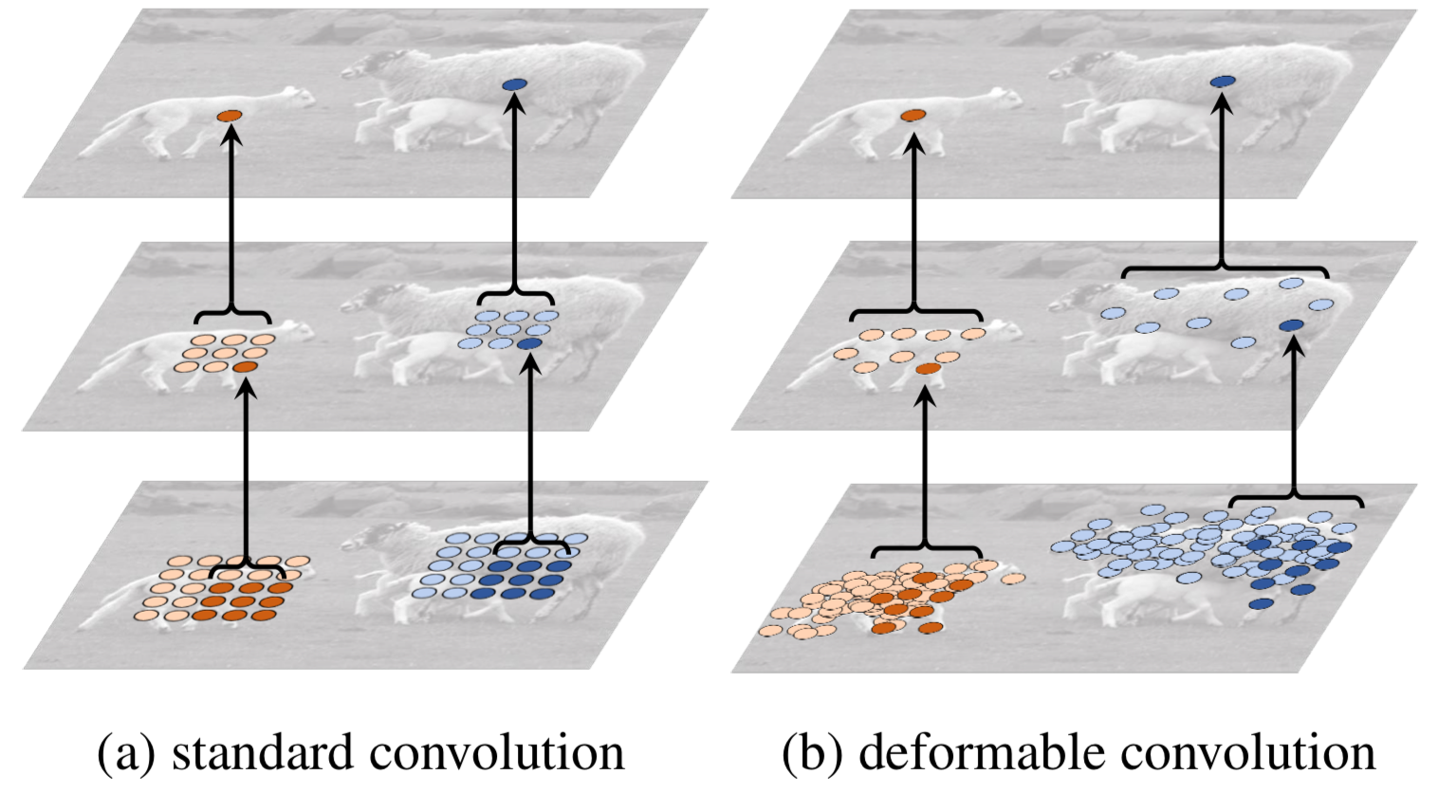
- deformable convolution이란?
-
따라서 우리는 Deformable DETR을 제안하고,
이는 DETR의 slow convergence와 high complexity 문제를 해결할 수 있다.
➡️ small object detection을 위해 high-resolution image feature를 encoder에 넣어도 deformable DETR은 high complexity 문제를 해결할 수 있고,
training convergence도 더욱 빠르게 만들 수 있다. -
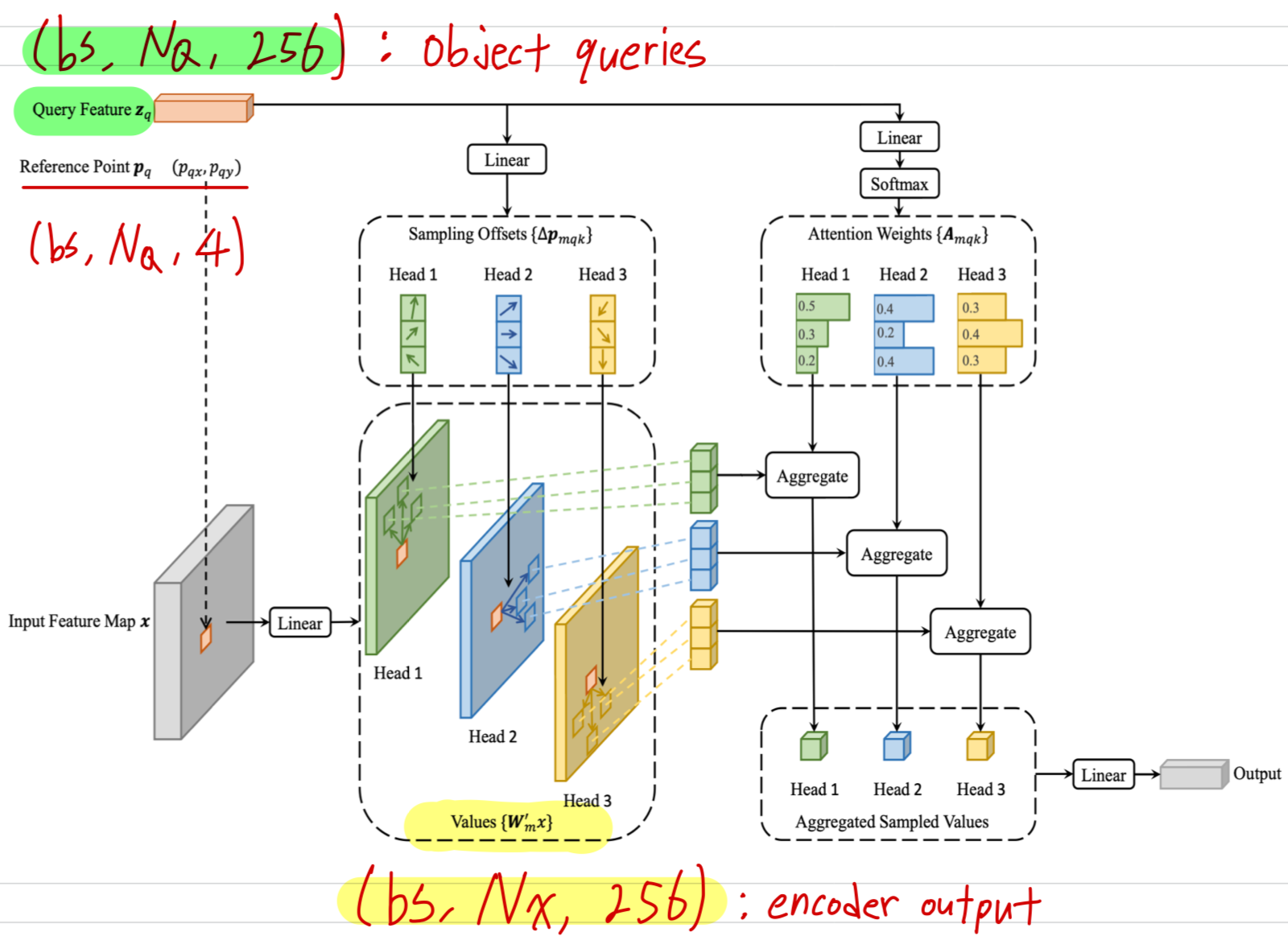
Deformable DETR을 구성하는 deformable attention module이 있는데,
deformable attention module은 feature map pixels에 대해서 중요한 핵심 pixel을
pre-filter(미리 filtering)한 a small set of sampling location에 집중한다.
각 qeury에 대해 고정된 소수의 key만 할당함으로써, convergence 문제와 feature spatial resolution으로 인한 high complexity 문제를 완화할 수 있다.

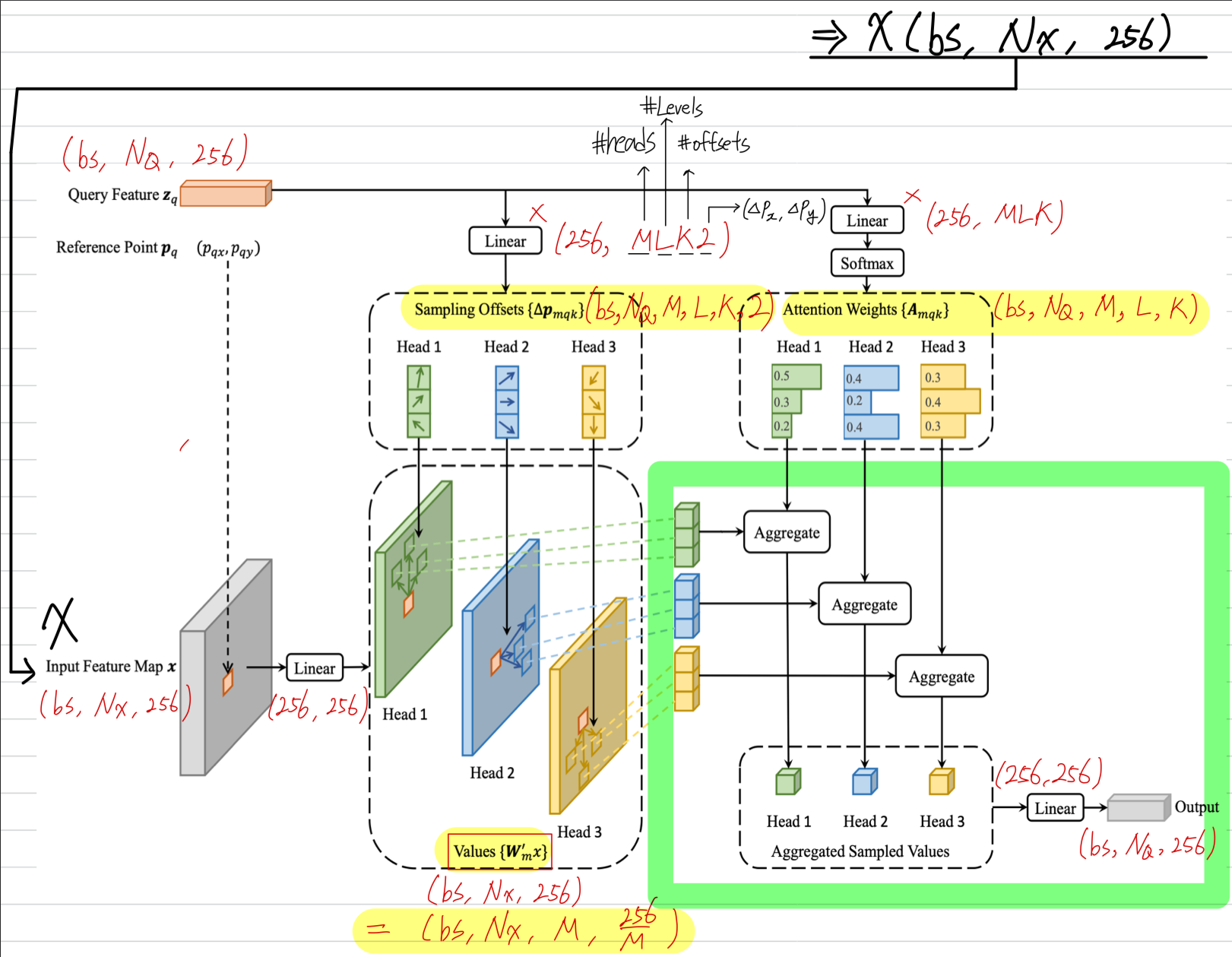
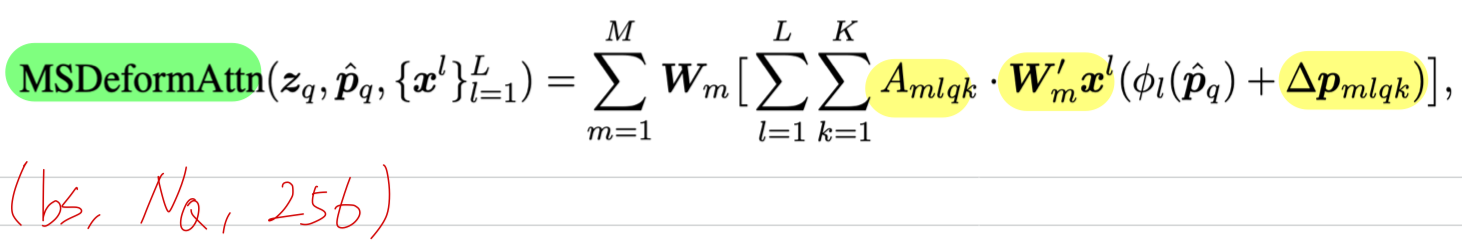 (초록색 형광) sampling offsets, Values, Attention Weights로 aggregate하여 output을 생성하는 code
(초록색 형광) sampling offsets, Values, Attention Weights로 aggregate하여 output을 생성하는 code
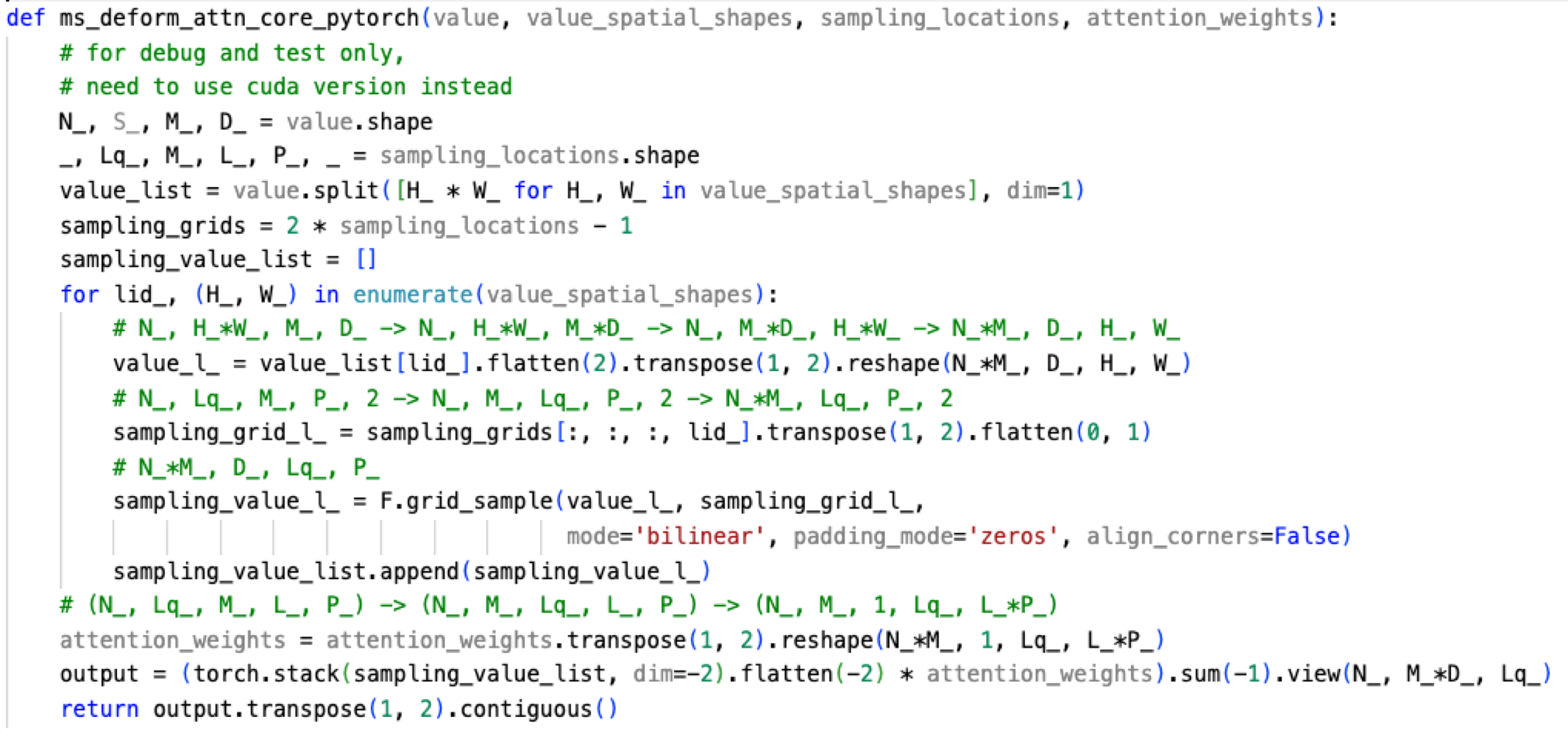 위 MSDEformAttnFunction에서 return한 output에 마지막으로 Linear projection.
위 MSDEformAttnFunction에서 return한 output에 마지막으로 Linear projection.
-
encoder는 위와 같은 Multi-Scale Deformable Attention Module이 개 stack되어 있고,
decoder는 기존 DETR과 같은 구조로 Self-Attention 이후에 Cross-Attention을 진행하는 layer가 개 stack되어 있음.
decoder에서 Cross-Attention을 진행할 때,
encoder의 output인 와 decoder의 object query 를
각각 key, query로 사용함.
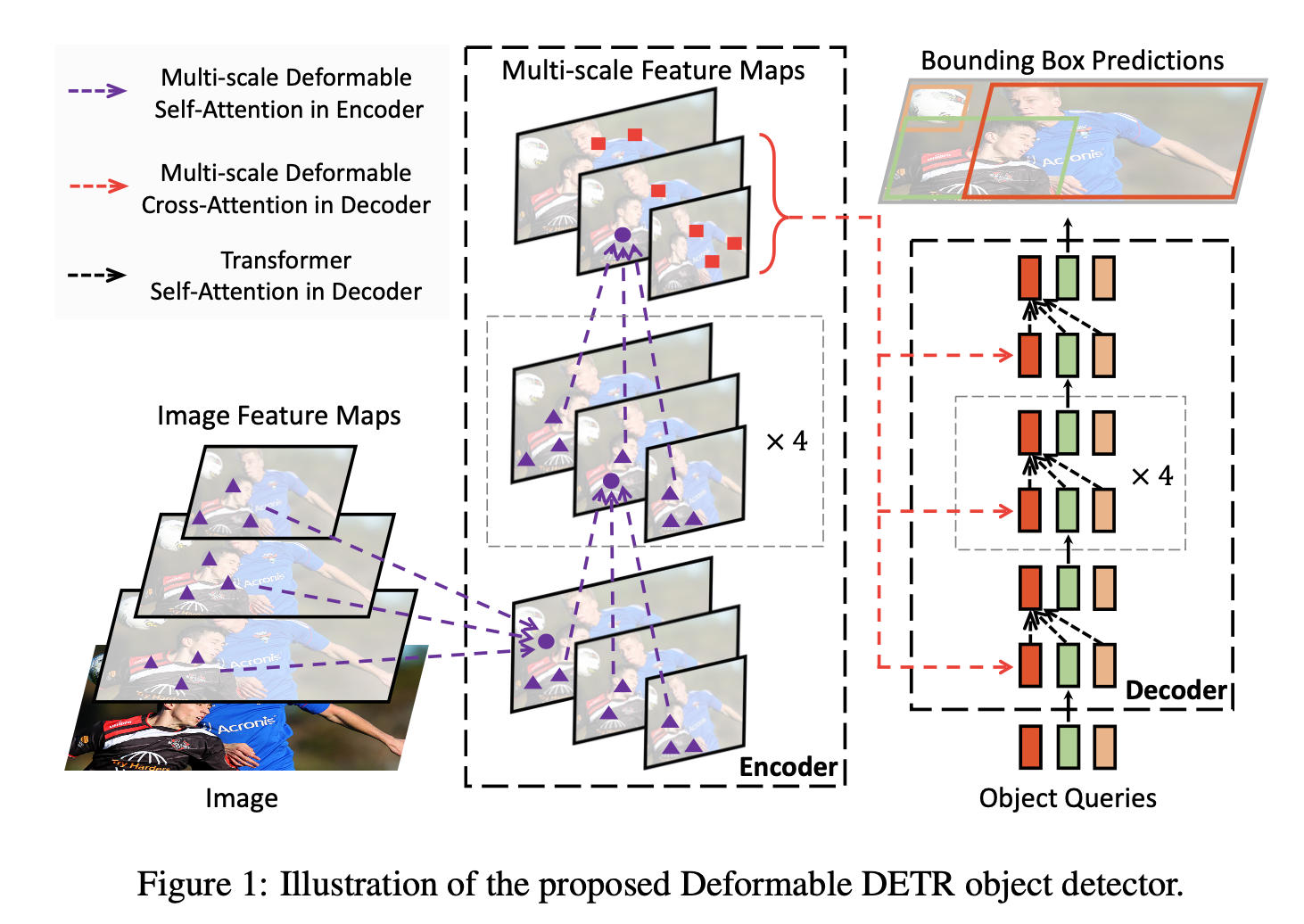 DETR에서는 decoder의 output feature map에 class_emb와 bbox_emb weight를 linear projection하여,
DETR에서는 decoder의 output feature map에 class_emb와 bbox_emb weight를 linear projection하여,
최종 prediction을 얻었다.
하지만 multi-scale deformable attention module은 reference point 주변에 image features를 뽑아내기 때문에,
optimization difficulty를 줄이기 위해 reference point에 대한 상대적인 offsets값으로 bounding box를 prediction하도록 detection head를 설계했다.
RT-DETR
Uncertainty-minimal Query Selection
- decoder
- 공통점 : DETR과 마찬가지로 self-attention과 cross-attention 구조로 이루어져 있다.
- 차이점 :
-
object queries initialization (with Uncertainty)
Encoder output feature map()에서
class probability 기준 top(=)의 index만 decoder의 object queries로 사용.
여기에 model이 noise에 더 잘 대응할 수 있도록 주는 denoising query 도 추가하여
➡️ 최종 decoder의 object queries는 ()가 된다. ()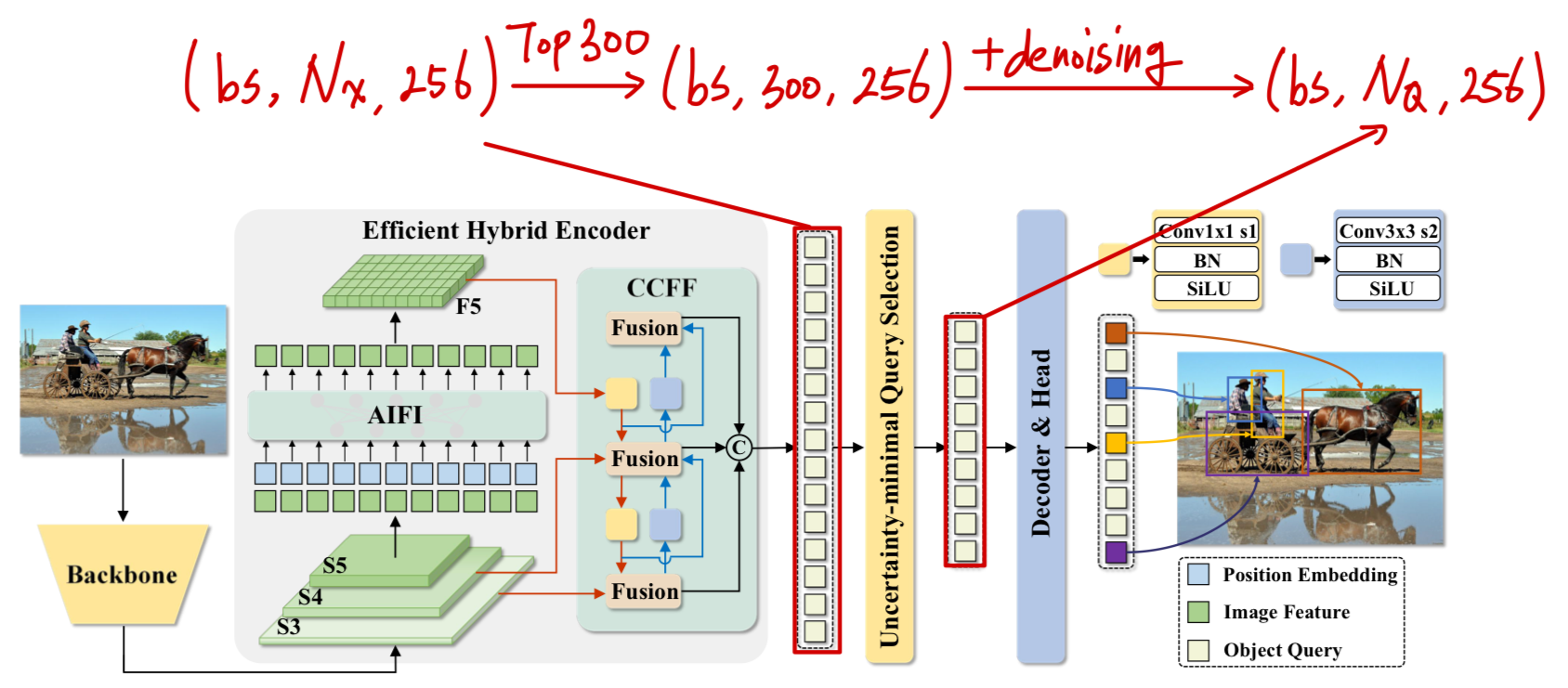 그래서 encoder의 output feature map이 중요하게 되었다.
그래서 encoder의 output feature map이 중요하게 되었다.
만약 encoder output의 uncertainty를 minimize할 수 있다면,
decoder에게 high-quality queries를 제공할 수 있어서 training convergence 속도가 빨라질 것이다.
따라서 encoder의 output feature map의 uncertainty를 최소화할 수 있도록 loss function에 다음의 loss를 추가하였다.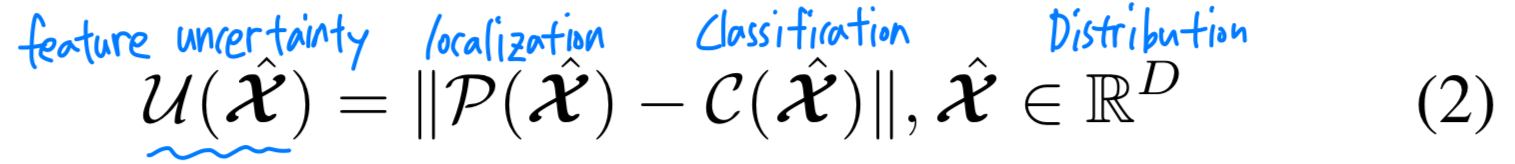 : encoder feature
: encoder feature
: localization
: classification
: the discrepancy between the predicted distribution of and
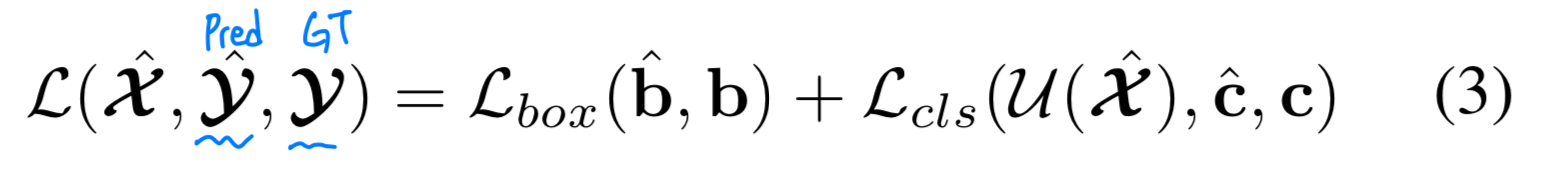 : prediction = {, } ( : category, : bounding box)
: prediction = {, } ( : category, : bounding box)
: ground truth
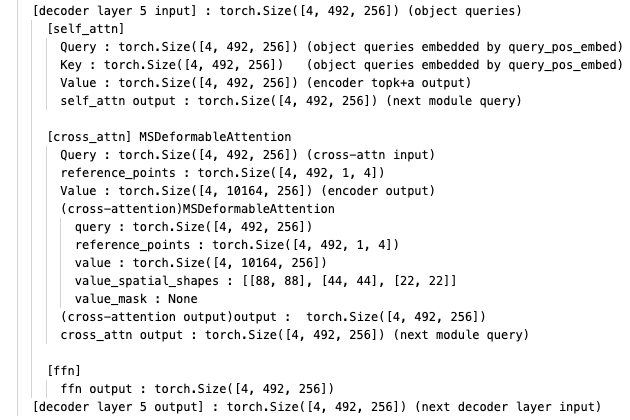
-
cross-attention이 MSDeformableAttention로 되어있다.
Deformable DETR에서와 똑같은 deformanble attention module을 사용한다.
Query는 object quries ()이고,
Value로는 encoder의 output feature map ()을 사용한다.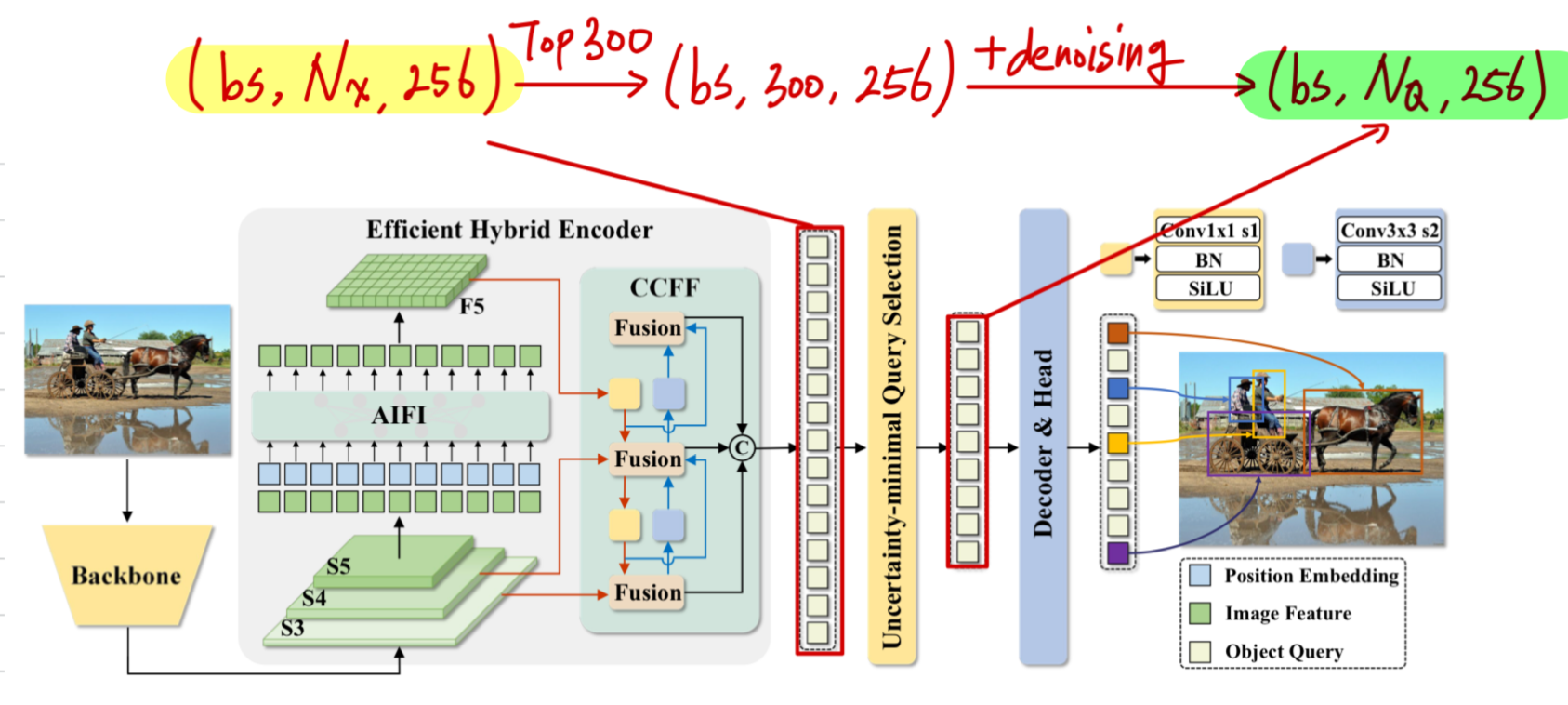
-
RT-DETR code 분석
1. Efficient Hybrid Encoder

2. Uncertainty-minimal Query Selection

3. Decoder
 ...
...